По технике решения задач числовой линии и методике обучения их решению

«Числовая линия»

Задания для учителей математики 5 - 9 классов:

Задание 1.Решите задачу: «Разность двух натуральных чисел равна 7, а их произведение – точный квадрат. Найти все пары таких чисел» несколькими способами.

Задание 2. Найдите ошибки в решении следующей задачи: «Найти все такие пары взаимно простых натуральных чисел a и b, что если к десятичной записи числа a приписать справа через запятую десятичную запись числа b, то получится десятичная запись числа, равного b/a», если таковые имеются. Укажите верное решение данной задачи.

Решение:

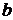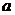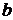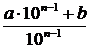Пусть десятичная запись числа состоит из n цифр. Тогда число, получающееся в результате приписывания к после запятой десятичной записи числа равно . По условию 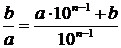. Преобразуем это уравнение следующим образом:

(*)

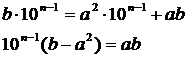
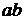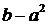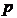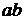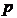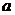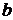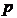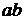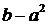Предположим, что числа и не взаимно просты. Тогда найдется простое число , которое является делителем этих чисел. Поскольку произведение делится на , каждый из множителей и делится на , но тогда они не могут быть взаимно простыми, так как это противоречит условию задачи. Итак, числа и взаимно простые (**).

Из условий (*) и (**) следует, что 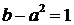. Но тогда 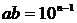. Возможны случаи:

1) 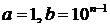. Тогда уравнение 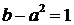принимает вид 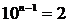и не иметт натуральных решений.

2) 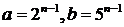. Для этой пары равенство 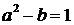принимает вид 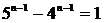и выполняется только при 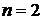. Покажем это. Поделим обе части уравнения на 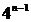, получим 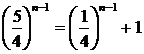. Предлагается самостоятельно построить обе функции (стоящую слева и стоящую справа в полученном равенстве) и привести данный чертеж в верном решении текущей задачи. Поскольку функция, стоящая в левой части последнего уравнения, является возрастающей, а в правой – убывающей, заключаем, что решение 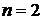единственное. Итак, .

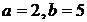Задание 3.Решите задачу: «Докажите, что если шестизначное число делится на 7, или на 11, или на 13 или на 37, то и число, полученное из него после перестановки первой цифры в конец, делится на то же самое число» и составьте вопросы для учащихся на этапе анализа условия или на этапе поиска решения.

Задание 4.Решите задачу: «Выясните, верно ли, что если целое число 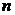не делится ни на 2, ни на 3, ни на 5, то разность 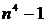делится на 240». Составьте и решите обратную к ней.

Задание 5.Решите задачу: «Найти все пары натуральных чисел a и b, удовлетворяющих равенству 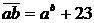». Составьте новые задачи из данной путем варьирования каждого из ее условий, решите их.

Задания для учителей математики 10 - 11 классов:

Задание 1.Решите задачу: «Найти все натуральные числа, являющиеся степенью двойки, такие, что после зачёркивания первой цифры их десятичной записи снова получается десятичная запись числа, являющегося степенью двойки» несколькими способами.

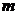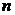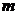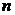Задание 2. Найдите ошибки в решении следующей задачи: «На клетчатой бумаге отмечен прямоугольник с вершинами в узлах сетки, со сторонами и , причём числа и взаимно простые и 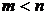. Диагональ этого прямоугольника не пересекает ровно 2020 клеток этого прямоугольника. Найти 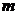и и 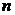», если таковые имеются. Укажите верное решение данной задачи.

Решение:

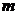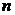По условию задачи числа и взаимно простые; отсюда заключаем, что диагональ прямоугольника не проходит через узлы сетки. Действительно, предположим, что это не так, и диагональ проходит через некоторый внутренний узел. Введём декартову систему координат, началом которой служит левая нижняя вершина прямоугольника, а оси координат проходят через стороны прямоугольника. Координаты правой верхней вершины прямоугольника будут 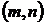, а координаты внутреннего узла, через который прошла диагональ, обозначим 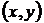. Из подобия треугольников получим: 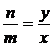, то есть 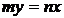. Отсюда 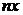делится на 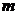. Поскольку 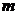и 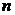взаимно просты, то 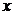должно делиться на 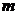, что невозможно ввиду 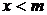. Указанное противоречие доказывает, что предположение о прохождении диагонали через внутренний узел прямоугольника ложно.

Легко подсчитать, что число клеток, пересекаемых диагональю, равно

.

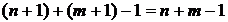Тогда число клеток, не пересекаемых диагональю, составляет

.

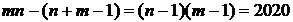Возможны следующие варианты представления числа 2020 в виде произведения натуральных чисел:

1) 1‧2020, тогда , ;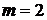

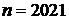2) 2‧1010, тогда 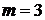, 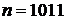– не являются взаимно простыми;

3) 4‧505, тогда , ;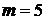

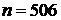4) 5‧404, тогда 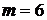, 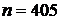– не являются взаимно простыми;

5) 10‧202, тогда , ;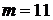

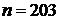6) 20‧101, тогда 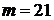, 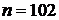– не являются взаимно простыми.

Ответ: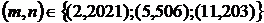

3.35

Задание 3.Решите задачу: «Произведение нескольких различных простых чисел делится на каждое из этих чисел, уменьшенное на 1. Чему может равняться это произведение?» и составьте вопросы для учащихся на этапе анализа условия или на этапе поиска решения.

Задание 4.Решите задачу: «Верно ли, что если у квадрата натурального числа последняя цифра нечетна, то его последняя цифра четна». Составьте и решите обратную к ней.

Задание 5.Решите задачу: «Докажите, что квадрат трехзначного числа 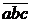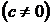оканчивается на 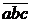тогда и только тогда, когда 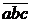равно 625 или 376». Составьте новые задачи из данной путем варьирования каждого из ее условий, решите их.