Классическая задача на условный экстремум. Необходимые и достаточные условия условного экстремума.

Пусть функция f определена в некоторой области G 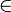R и точкаP 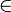G. Значения функции в этой точке называется (локальным) минимумом, соответственно, локальным максимумом функции f в G тогда и только тогда, когда существует некоторая окрестность U(P) 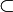G

Точки P такая, что для всех точек P 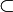U(P) имеет место соответственно

f(P) >f(Pо). Максимум или минимум функции f называется также (локальным) экстремумом функции f в G. Значение локального экстремума функции f в точке Pо является наименьшим или наибольшим значением функции в некоторой окрестности точки Pо, однако оно не совпадает, вообще говоря, с наименьшим или наибольшим значением функции в области G.

Необходимые условия существования экстремума. Если f(Pо) есть экстремум функции f, дифференцируемой по каждой из координат в некоторой окрестности U(Pо) точки Pо, то имеет место f(Po)=0; (i=1,..,n)

Достаточное условие экстремума. Пусть в некоторой области, содержащей Pо(хо, уо), функция f(х,у) имеет непрерывные частные производные до третьего порядка включительно, пусть кроме того, точка Pо(хо, уо) является критической точкой функции f(х,у) т.е.

Тута ф – ла))

Метод множителей Лагранжа для решения классической задачи на условный экстремум.

Метод множителей Лагранжа, метод нахождения условного экстремума функции 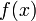, где 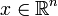, относительно 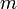ограничений 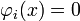, где 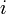меняется от единицы до .

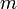§ Составим функцию Лагранжа в виде линейной комбинации функции 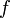и функций 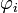, взятых с коэффициентами, называемыми множителями Лагранжа — :

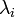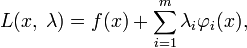
где .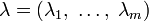

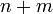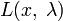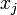§ Составим систему из уравнений, приравняв к нулю частные производные функции Лагранжа по и .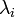

§ Если полученная система имеет решение относительно параметров 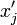и 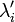, тогда точка 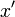может быть условным экстремумом, то есть решением исходной задачи. Заметим, что это условие носит необходимый, но не достаточный характер.

Двумерный случай

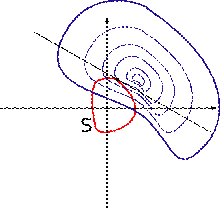
Линии уровня 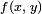и кривая .

Пусть требуется найти экстремум некоторой функции двух переменных 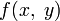при условии, задаваемом уравнением 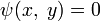. Мы будем считать, что все функции непрерывно дифференцируемы, и данное уравнение задает гладкую кривую 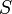на плоскости 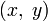. Тогда задача сводится к нахождению экстремума функции 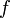на кривой 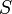. Будем также считать, что 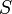не проходит через точки, в которых градиент 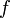обращается в .

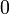Нарисуем на плоскости 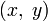линии уровня функции 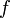(то есть кривые 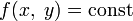). Из геометрических соображений видно, что экстремумом функции 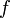на кривой 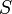могут быть только точки, в которых касательные к 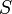и соответствующей линии уровня совпадают. Действительно, если кривая 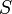пересекает линию уровня 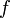в точке 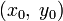трансверсально (то есть под некоторым ненулевым углом), то двигаясь по кривой 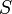из точки 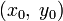мы можем попасть как на линии уровня, соответствующие большему значению 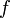, так и меньшему. Следовательно, такая точка не может быть точкой экстремума.

Тем самым, необходимым условием экстремума в нашем случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функци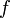й и 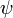в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:

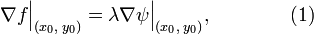
где 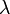— некоторое число, отличное от нуля, и являющееся множителем Лагранжа.

Рассмотрим теперь функцию Лагранжа , зависящую от 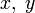и :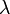

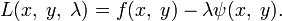
Необходимым условием ее экстремума является равенство нулю градиента 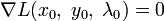. В соответствии с правилами дифференцирования, оно записывается в виде

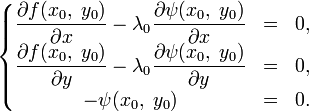
Мы получили систему, первые два уравнения которой эквивалентны необходимому условию локального экстремума (1), а третье — уравнению 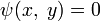. Из нее можно найти 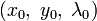. При этом 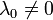, поскольку в противном случае градиент функции 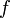обращается в нуль в точке 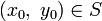, что противоречит нашим предположениям. Следует заметить, что найденные таким образом точки 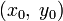могут и не являться искомыми точками условного экстремума — рассмотренное условие носит необходимый, но не достаточный характер. Нахождение условного экстремума с помощью вспомогательной функции 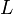и составляет основу метода множителей Лагранжа, примененного здесь для простейшего случая двух переменных. Оказывается, вышеприведенные рассуждения обобщаются на случай произвольного числа переменных и уравнений, задающих условия.

На основе метода множителей Лагранжа можно доказать и некоторые достаточные условия для условного экстремума, требующие анализа вторых производных функции Лагранжа.