Выпуклость и вогнутость кривой. Точки перегиба.

Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой. Рис 1На рисунке показана иллюстрация приведенного выше определения.

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла). Доказательство. Пусть х₀ Î (a, b). Проведем касательную к кривой в этой точке. Уравнение кривой: y = f(x); Уравнение касательной: 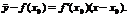Следует доказать, что 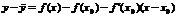. По теореме Лагранжа для f(x) – f(x₀): 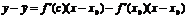, x₀ < c < x. 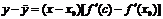По теореме Лагранжа для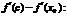 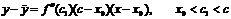Пусть х > x₀ тогда x₀ < c₁ < c < x. Т.к. x – x₀ > 0 и c – x₀ > 0, и кроме того по условию 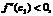, следовательно, 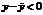. Пусть x < x₀ тогда x < c < c₁ < x₀ и x – x₀ < 0, c – x₀ < 0, т.к. по условию 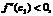то 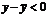.Аналогично доказывается, что если f¢¢(x) > 0 на интервале (a, b), то кривая y=f(x) вогнута на интервале (a, b).

7. Определение точек перегиба. Доказать необходимый и достаточный признаки точек перегиба.

Точкой перегиба

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная пересекает кривую. Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба. Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.

8. Асимптоты графика функции. Наклонные асимптоты. Вертикальные асимптоты. Привести примеры

Асимптоты.

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой. Определение. Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю. Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой. Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции 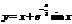. Ее наклонная асимптота у = х. Рис 1 Рассмотрим подробнее методы нахождения асимптот кривых. Вертикальные асимптоты. Из определения асимптоты следует, что если предел или один из односторонних пределов раны бесконечности, то прямая х = а – асимптота кривой y = f(x). Например, для функции 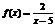прямая х = 5 является вертикальной асимптотой. Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b. Рис 2Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда MQ = y – ордината точки кривой, NQ = 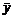- ордината точки N на асимптоте.

1. Определение первообразной. График первообразной. Определение неопределенного интеграла. Теорема существования неопределенного инте­грала (без док-ва). Свойства неопределенного интеграла.