Производная суммы (разности) функций

Приложение скалярного произведения

Угол между векторами: cos α = a*b / |a|*|b|

Длина вектора: |a|² = a²_x + a²_y + a²_z

№15. Векторное произведение векторов.

C = A x B

1) Вектор С действует вдоль прямой перпендикулярой A и B = > C перпендик. A и B

2) С по длине равен площади параллелограмма С = S = |A| * |B| sin α

3) A, B, C –правая тройка A x B = -B x A

Свойства:

а) 1. a*b= -b*a

2. λ[a*b]= λ*a*b=a* λ*b

3. a*[b+c]=a*b+a+c

4. i*i=j*j=k*k=0

б) i*i=k; j*k=i; k*i=j P.S везде вектора нарисовать

№16.Смешанное произведение векторов и его свойства.

Умножим вектора а´b, а затем полученный вектор u скалярно умножим на векторс, тогда получим число, которое наз. смешанным произведением a,b,c: (a´b)c-число; a={a₁+a₂+a₃}; b={b₁+b₂+b₃}; c={c₁+c₂+c₃}; u={u₁+u₂+u₃}; (a´b)c=uc= u₁c₁+u₂c₂+u₃c₃=(*).Св-ва: 1)От перестановки двух сомножителей смешанное произведение меняет знак, сохраняя абсолютную величину(т.к. при этом меняются две строки определителя); 2)Операции скалярного и векторного умножений в смешанном произведении можно поменять местами т.к. по св-ву (1) (a´b)c=-(c´b)a=(b´c)a=a(b´c),поэтому смешанное произведение часто записывают abc, опустив скобки и знаки действий, т.к. безразлично какие два рядом стоящих вектора перемножаются векторно, а какие скалярно. Выясним геометрический смысл смешанного произведения. Пусть OA=a, OB=b, OC=c–некомпланарны(правая связка)(рис.1). Т.к. векторы a,b,c-правая связка, то вектор uбудет направлен в ту же сторону, что и с. V_п=S_ABCD H=|(a´b)|пр_uc=|u|пр_uc=uc=(a´b)c.Таким образом V_п=±(a´b)cпричём «+» берётся если a,b,c-правая связка, и «-» если левая.V_п=|(a´b)c|; V_пир=1/6|(a´b)c| (рис.2). 1)Пусть a,b,c-компланарны, или какие-то два из трёх векторов коллинеарны: a||bÞu=a´b=0;2)Или слежит в плоскости двух других векторов аи b, т.е. проекция вектора сна вектор u пр_uc=0. Но и в том и в другом случае имеем, что смешанное произведение a,bи cбудет равно (a´b)c=|u|пр_uc=0.Обратно: (a´b)c=0Þa´b=0илипр_uc=0. a,b,c -компланарныÛ(a´b)c=0или (*1).

Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю.

№17. НЕТ

№18. Уравнение прямой на плоскости с угловым коэффициентом, проходящей через две две заданные точки.

Система двух линейных уравнений {Ax+By+Cz+D=0(a), A₁x+B₁y+C₁z+D₁=0(b)},в которых коэффициенты при x,y,zне пропорциональны, определяют некоторую прямую lв пространстве, как линию пересечение плоскостей a и b.Уравнения {Ax+By+Cz+D=0(a), A₁x+B₁y+C₁z+D₁=0(b)}наз. общими уравнениями прямой в пространстве. Пусть прямая lпроходит через две точки M₁(x₁;y₁;z₁) иM₂(x₂;y₂;z₂), тогда в качестве направляющего вектора прямой lпримем вектор М₁М₂={x₂–x₁;y₂–y₁;z₂–z₁}Þ l: (x–x₁)/(x₂–x₁)=(y–y₁)/(y₂–y₁)=(z–z₁)/(z₂–z₁).

№19. Общее уравнение прямой на плоскости, !уравнение прямой в отрезках!.

Система двух линейных уравнений {Ax+By+Cz+D=0(a), A₁x+B₁y+C₁z+D₁=0(b)},в которых коэффициенты при x,y,zне пропорциональны, определяют некоторую прямую lв пространстве, как линию пересечение плоскостей a и b.Уравнения {Ax+By+Cz+D=0(a), A₁x+B₁y+C₁z+D₁=0(b)}наз. общими уравнениями прямой в пространстве.

№20. Угол между 2-мя прямыми на плоскости, условия коллинеарности и ортогональности прямых на плоскости.

L:y=k₁x+b₁ m:y=k₂x+b₂ Найдем угол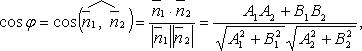

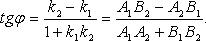
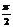
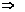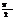
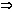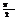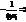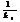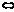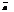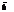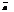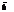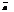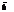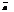
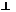
1)Если прямая l‌‌║m, то α₁₌α₂→tgα₁=tgα₂→k₁=k₂ ; l║m↔ k₁=k_2. 2) l┴m, то φ= α_1-α₂+ tgα₂=tg(α₁+ )=-ctgα₁= k₂=- . l┴m k₁k₂=-1. Если векторы и перпендикулярны плоскости Р, то они коллениарны. Если угол между ненулевыми векторами и равен 90⁰, то векторы и называют ортогональными и пишут 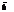. По определению, векторы 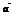и 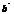также считают ортогональными, если один из них нулевой.

№21. Расстояние от точки до прямой на плоскости.

L: xcosβ+ysinβ-p=0 M₁(x₁,y₁) d=‌‌│MK│=│P₀N│‌(рис.) Найдем проекцию точки М₁ на ось ON пр_ONM₁=x₁cosβ+y₁sinβ. OP₀=p+│NP₀│. x₁cosβ+y₁sinβ= p+│NP₀│→d+ x₁cosβ+y₁sinβ-p→для того чтобы найти расстояние от точки до прямой надо в левую часть нормального уравнения прямой подставить координаты данной точки. d= │x₁cosβ+y₁sinβ-p│. Если L: xcosβ+ysinβ+с=0 , то приведя это уравнение к нормальному виду получим. d=│ │.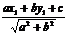

№22. Вывод уравнения плоскости, проходящей через данную точку перпендикулярно данному вектору.Общее уравнение плоскости .

!Общее уравнение плоскости!. Пусть дана плоскость a,проходящая через точку М₀, заданную радиус-вектором r₀={x₀;y₀;z₀}, перпендикулярно вектору n={A;B;C}.Проведём радиус-вектор r={x;y;z}в произвольную точку Мэтой плоскости. Вектор М₀М=r–r₀ лежит в плоскости aи ^ вектору n(рис.1)Þих скалярное произведение М₀Мn=0. Выражая скалярное произведение векторов через их координаты, получем: A(x-x₀)+B(y-y₀)+C(z-z₀)=0

№23. Уравнение плоскости, проходящей через три данные точки.

Пусть дана плоскость, не параллельная ни одной из координатных осей и отсекающая на осях неравные 0 отрезки: ОМ=а, ON=b, OP=c. Уравнение этой плоскости имеет вид: a: Ax+By+Cz+D=0; A¹0, B¹0, C¹0, D¹0.Т.к. М(а;0;0)Îa, Aa+B0+C0+D=0ÞA= -D/a. Т.к. N(0;b;0)Îa, A0+Bb+C0+D=0ÞB= -D/b. Т.к. P(0;0;c)Îa, A0+B0+Cc+D=0ÞC= -D/c.Из a: Ax+By+Cz+D=0следует: –Dx/a–Dy/b–Dz/c+D=0|:(-D); x/a+y/b+z/c=1–уравнение плоскости в отрезках.

№24. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.

Пусть даны две непараллельныеплоскости: a:Ax+By+Cz+D=0, b: A₁x+B₁y+C₁z+D₁=0, a не|| b, N₁^a, N₂^b. Линейный угол gдвугранного угла, образованного этими плоскостями имеет стороны перпендикулярные к нормальным векторамN₁, N₂этих плоскостейÞУголgмежду плоскостями равен углу между векторами g=(N₁^Ù N₂), или дополняет его до 180°; g=180°-(N₁^Ù N₂)Þcosg=±( N₁N₂)/( |N₁||N₂|)=|AA₁+BB₁+CC₁|/(ÖA²+B²+C²ÖA₁²+B₁²+C₁²).1)Если a||bÞN1||N2ÛA/A₁=B/B₁=C/C₁;2)Если a^bÞ N₁^N₂ÛN₁N₂=0 т.е. AA₁+BB₁+CC₁=0.

№25. Расстояние от точки до плоскости.

Расстояние от точки до плоскости --- это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Если плоскость задана уравнением 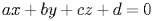, то расстояние 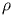от точки 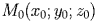до этой плоскости можно вычислить по формуле
.

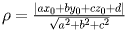Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и

В(3, 2, -1) перпендикулярно плоскости х + у + 2z – 3 = 0.

Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости (A, B, C). Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

Таким образом, вектор нормали (11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11×2 + 7×1 - 2×4 + D = 0; D = -21.

Итого, получаем уравнение плоскости: 11x - 7y – 2z – 21 = 0.

№26. Общие уравнения прямой в пространстве.

Система 2-х линейных уравнений (Ax+By+Cz+D=0 (α) и A₁x+B₁y+C₁z+D₁=0 (β) (*)). Система 2-х линейных уравнений в которых коэффициенты не пропорциональны определить некоторую прямую l в пространстве как линия пересечения плоскости α и β. Уравнение (*) называется общим уравнением прямой в пространстве.

№27. Канонические и параметрические уравнения прямой в пространстве.

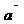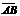= =(x_B-x_A; y_B-y_A; z_B-z_A).

x=x₀+mt, y=y₀+nt, z=z₀+pt. ß параметрическое(системой записать)

Х-Х0/m=Y-Y0/n=Z-Z0/P ß Каноническое

№28. Переход от общих уравнений прямой в пространстве к каноническим.

Пусть z=0 M(-1;-1;0) .

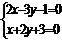
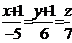
№29. Уравнение прямой в проекциях. Уравнение прямой проходящей через 2 точки.

M₁(x₁; y₁) M₂(x₂; y₂), x₁≠x₂, т.е. прямая М₁М₂ не параллельна OY . Согласно предыдущему уравнение любой не вертикальной прямой проходящих через M₁(x₁; y₁) имеет вид y-y₁=k(x-x₁) (*). Т.к. точка М₂ принадлежит данной прямой, то ее координаты удовлетворяют уравнению прямой. Т.е. y₂-y₁=k(x₂-x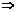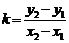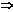₁) .(*) y y₁=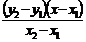

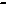
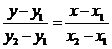
№30. Угол между 2-мя прямыми в пространстве. Условия параллельности и перпендикулярности 2-х прямых в пространстве.

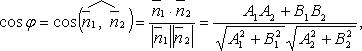
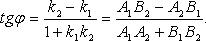
Параллельность и перпендикулярность. В случае перпендикулярности прямых L₁ и L₂ их нормальные векторы также перпендикулярны, т.е. справедливо равенство (n₁, n₂)=0 или A₁A₂+B₁B₂=0. В случае параллельности L₁ и L₂ их нормальные векторы коллинеарны, т.е. справедливо равенство n₁=λn₂. Переходя к координатам этих векторов, получаем, что A₁=λa₂, B₁=λB₂, или .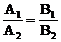

№31. №32. Расстояние между 2-мя параллельными прямыми в пространстве. Расстояние между 2-мя скрещивающимися прямыми.

l: xcosβ+ysinβ-p=0 d│MK│=│P₀N│(рис). Найдем проекцию точки М₁ на ось ON пр_ONM₁=x₁cosβ+y₁sinβ, OP₀=p+│NP₀│, x₁cosβ+y₁sinβ=p+│NP₀│ 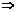d= x₁cosβ+y₁sinβ-p 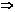для того чтобы найти расстояние от точки до прямой надо в левую часть нормального уравнения прямой подставить координаты данной точки т.е. d= x₁cosβ+y₁sinβ-p. Если l: xcosβ+ysinβ-p=0, то приведя это уравнение к нормальному виду получим: d= .

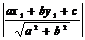№33. Условия параллейности и перпендикулярности прямой и плоскости. Точка пересечения прямой и плоскости.

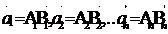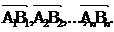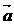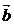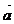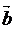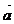
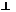
называют параллейными(коллинеарными) если коллениарны(параллели) изображающие их направленные отрезки Если угол между ненулевыми векторами и равен 90⁰, то векторы и называют ортогональными(перпендикулярными) и пишут 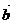. По определению, векторы 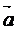и 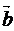также считают ортогональными, если один из них нулевой.

L: 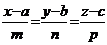; α: Ax+By+c+D=0; Найдем точки их пересечения, прейдем каноническое уравнение прямой к параметрической. 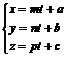(V), и выражаем для (x; y; z) подставим в уравнение плоскости получим уравнение относительно неизвестного параметра t, затем подставим найденное значение t в (V) получим координаты в точках пересечения прямой и плоскости

№34. №35 Не совсем то, что надо.

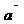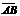= =(x_B-x_A; y_B-y_A; z_B-z_A).

x=x₀+mt, y=y₀+nt, z=z₀+pt. ß параметрическое(системой записать)

Х-Х0/m=Y-Y0/n=Z-Z0/P ß Каноническое

№36. Полярная система координат. Это вообще что за херь?? НЕТУ.

№37. Переменные и постоянные величины. Определение функции. Способы задания функций.

Переменной величиной называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной. В математике постоянная величина часто рассматривается как частный случай переменной, у которой все численные значения одинаковы. Если каждому значению переменной x, принадлежащему некоторой области, соответствует одно определенное значение другой переменной y, то y есть функция от x или, в символической записи, y=f(x), y=φ(x), и т.п. Способы задания функции. 1) Аналитический. 2) Графический. 3) Табличный. 4) Словесно.

№38. Определение предела переменной величины. Теорема о единственности предела. Теорема о пределе промежуточной переменной.

Предел переменной величины. Определение: Постоянное число a называют пределом переменной величины x, если для любого e > 0 можно указать такое значение x, что все последующие значения будут удовлетворять неравенству |x-a| < e.

У одной переменной двух пределов не существует.(Доказательство)

Теорема (единственность предела) Если функция f в точке а имеет предел, то этот пределединственный.

Доказательство: метод от противного limx→af(x)=b,limx→af(x)=c,b/=c . Возьмем ε=∣b−c∣ , по определению и свойству окрестности найдется выколотая окрестность т. а Uo(a,δ), в которой одновременно будут выполняться неравенства ∣f(x)−b∣<2∣b−c∣∣f(x)−c∣<2∣b−c∣ , тогда в точках этой же окрестности ∣b−c∣=∣(b−f(x))+(f(x)+c)∣≤∣f(x)−b∣+∣f(x)−c∣<2∣b−c∣+2∣b−c∣=∣b−c∣ противоречие (от неправильно допущения)

ТЕОРЕМА (о пределе промежуточной функции)

Если 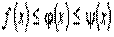на 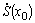и существуют 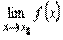и 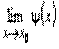и их значения конечны и равны, то существует предел промежуточной функции 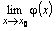и его значение совпадает со значением пределов оценивающих слева и справа функций.
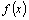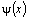используя определение предела по Коши для функций и при .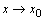

№39. ОГРАНИЧЕННОСТЬ ПЕРЕМЕННЫХ, ИМЕЮЩИХ КОНЕЧНЫЙ ПРЕДЕЛ.

Пусть xŠa или xŠ∞.

Теорема 1: предел алгебраической суммы конечного числа переменных=сумме пределов этих переменных,т.е. lim(U₁+U₂+…+U_n)=limU₁+limU₂+…+limU_n.Док-во: пусть предел U=а и пусть limV=b, тогда по св-ву 7(теорема о связи) имеем U=a+a и V=b+b-бесконечно малые величины. Рассм.переменную величину: U+V=(a+a)+(b+b)=(a+b)+(a+b)=>а это по теореме по связи означает: lim(U+V)=(a+b)=limU+limV. Пример:lim_xŠ∞(x²+2x)/x²=[∞/∞] =lim_xŠ∞(1+²/_x)= lim_xŠ∞1+lim_xŠ∞²/_x =1+0=1.

Теорема 2: предел произведения конечного числа переменных=произвед.пределов этих переменных,т.е. lim(U₁*U₂*…*U_n)=limU₁*limU₂*…*limU_n. Док-во:пусть limU=а=>по св-ву(7) U=a+a,где a-б.м.в.; limV=b=>по св-ву(7) V=b+b,где b-б.м.в. Рассм. U*V=(a+a)*(b+b)=ab+ab+ba+ab= число+б.м.в.+б.м.в.+б.м.в.,т.е. переменную величину U,V мы смогли представить в виде суммы нек-го числа аb и б.м.в., а это по теореме о связи означает, что lim(U*V)=a*b=limU*limV, теорема доказана.

Следствие: постоянный множитель можно выносить за знак предела. Пусть limU=a, a c=const=>limC=C. Рассм. lim(C*U)=limC*limU=C*limU=C*a. Пример: lim_xŠ25x³=5lim_xŠ2x²=5*8=40.

Теорема 3: предел частного 2-х ф-ций =частному пределов этих переменных если предел знаменателя отличен от 0,т.е. lim(U/V)=limU/limV,где limV≠0. Док-во: пусть limU=а=> U=a+a,где a-б.м.в.; limV=b=> V=b+b,где b-б.м.в. Рассм. U/V=(a+a)/(b+b)=a/b+((a+a)/(b+b)-a/b)=a/b+((ab+ab-ab-ab)/b(b+b)) =a/b+((ab-ab)/ b(b+b))-(б.м.в.)=>lim(U/V)=a/b=limU/limV-ч.т.д.

Пример: 1),2),3)-(см.№1на др.стороне).

Теорема 4: если между соответствующими значениями 3-х ф-ций: U(x), Z(x),V(x) выполняется нер-во U≤Z≤V и при этом ф-ции U и VŠк одному и тому же limb при хŠa или xŠ∞, то и ф-ция Z при хŠa или xŠ∞ будет стремится к тому же самому limb. Док-во: пусть хŠa. По усл: U≤Z≤V, тогда из этого нер-ва =>U-b≤Z-b≤V-b. По усл: lim_хŠaU=b=>(по опр.) это означает, что для любого ε>0 cущ.окрестность точки а в кот-ой будет выполняться нер-во |U-b|<ε. Или –ε<U-b<ε (1). По усл: lim_хŠaV=b=> для выбранного ε сущ.окрестность точки а в кот-ой выполняется нер-во: |V-b|<ε. –ε<V-b<ε (2), тогда в меньшей из этих 2-х окрестностей будут выполняться оба нер-ва (1) и (2). (см.№2 на др. стороне).

Теорема 5: если при хŠa или xŠ∞ ф-ция y принимает неотрицат.знач-ия а имеет своим пределом число b, то b≥0,т.е. y≥0, lim_{хŠaилиxŠ∞}y=b=>b≥0. Док-во: предположим противное: пусть b<0, тогда |y-b| будет ≥|b|,т.е. модуль разности |y-b| больше положительного числа модуль |b|,т.е. модуль разности не стремится к 0 при хŠa или xŠ∞=> число b не может быть пределом ф-ции y, что подтверждает условие=>наше предположение не верно и b≥0. Аналогично доказывается: y≤0, lim_{хŠaилиxŠ∞}y=b=>b≤0.

Теорема 6: если между соответствующими знач-ми 2-х ф-ций U и V выполняется нер-во U(x)≤V(x), то limU≤limV при хŠa или xŠ∞. Док-во: по усл: V-U≥0. Рассм. lim(U-V)≥0, но limV-limU≥0=>limV≥limU.ч.т.д.

№40. Бесконечно малые (б.м.) и их свойства.

Опр:ф-ция y=a(x) назыв.б.м. при хŠа, если lim_хŠаa(x)=0. Основные св-ва. Алгебраическая сумма любого конечного числа бесконечно малых ф-ций есть бесконечно малая ф-ция. 1)пусть U(x)= a(x)+b(x), где lim_хŠаa(x)=0 и lim_хŠаb(x)=0,т.е.нам надо доказать, что для любого e>0 сущ.число δ>0, такое что для всех х удовл.нер-ву 0<|х-а|<δ будет выполнится нер-во |U(x)-0|<e или |U(x)|<e. Докажем: т.к. lim_хŠаa(x)=0=>то по определению это значит,что для любого e>0 сущ.δ₁-окрестность точки а, в кот-ой выполняется нер-во |a(х)|<e/2. Т.к. lim_хŠаb(x)=0,то для выбранного e сущ.δ₂-окрестность точки а, в кот-ой выполняется нер-во |b(х)|<e/2. Обозн.через δ наименьшее из чисел δ₁ и δ₂. δ=min|δ₁,δ₂|, тогда в δ окрестности точки “а” будет выполнятся нер-во: |U(x)|=|a(x)+b(x)|≤|a(x)|+|b(x)|<e/2+e/2=e, т.е.|U(x)|<e=>lim_xŠaU(x)=0,т.е.U(x)-бесконечно малая ф-ция. Аналогичное док-во для случая когда lim_хŠаa(x)=0 и lim_хŠаb(x)=0. 2)Произведение б.м.ф-ции при хŠа (или хŠ∞). На ограниченную ф-цию есть б.м.ф-ция. Пусть lim_хŠаa(x)=0=>,что для любого e>0 сущ.δ₁-окрестность точки а, в кот-ой выполняется нер-во |a(х)|<e/М,где M>0. y=f(x)-ограниченная, то по определению это означает, что сущ.такое δ₂-окрестность точки а, в кот-ой выполняется нер-во |f(x)|<M,M>0. Обозн.через δ наименьшие из чисел δ₁,δ₂,тогда в δ-окрестности точки “а” будет выполняться нер-во: |a(x)*f(x)|=|a(x)|*|f(x)|<eM/M=>a(x)*f(x)-бесконечно малая величина. 3)a(x)/f(x)-бесконечно малая ф-ция a(х) и ф-ция lim_хŠаf(x)=b≠0-есть бесконечно малая ф-ция. Дейст-но пусть lim_хŠаa(x)=0,а lim_хŠаf(x)=b≠0=>1/f(x)-ограниченная ф-ция, а отсюда следует, что a(x)/f(x)=a(х)*1/f(x)=беск.алая ф-ция. 4)произведение любого конечного числа бесконечно малое есть б.м. 5)произвед.б.м.ф.на const.есть б.м.ф. 6)если a(х)-б.м.в. при хŠа (или хŠ∞), то 1/a(x)-б.б.в.при хŠа (или хŠ∞). 7)если при lim_хŠаf(x)=b, то f(x)=b+a(x),где lim_хŠаa(x)=0.

№41. Бесконечно большие ф-ции,их связь с бесконечно малыми.

Опр.ф-ция f(x)назыв.бесконечно большой(б.б.) при хŠа (т.е.Š∞ при хŠа), если для любого числа М>0, сущ.число δ>0 для всех х удовл.нер-ву 0<|x-a|<δ будет выполняться |f(x)|>M,т.е. lim_xŠaf(x)=∞,если -M>0 сущ.δ>0, такое что х-; 0|х-а|<δ;|f(x)|>М.(см.рис.1.). В этом случае пишут lim_xŠaf(x)=∞ или f(x)Š∞ при хŠа. если ф-ция f(x) явл.б.б. и при этом сохраняется только “+” или только “—”,знач.,то в этом случае пишут lim_xŠaf(x)=+∞ или lim_xŠaf(x)=-∞. Докажем: lim_xŠ1 1/(1-x)²=+∞. Берём любое число M>0 и рассм.|f(x)|=+∞, |f(x)|>M; 1/(1-x)²>M; (1-x)²<1/M; |1-х|<√1/М=δ=>что в качестве δ можно взять √1/М. Для любого х, отличного от 1 наша ф-ции будет>0,т.е.ф-ция f(x)-б.б. и f(x)>0=>предел нашей ф-ции=+∞,т.е. -х≠1 1/(1-х²)>0=>f(x)-б.б.в. и f(x)>0 =>lim_xŠ1f(x)=+∞. Если ф-ция f(x)Š∞ при хŠ∞, то пришут:lim_xŠ∞f(x)=∞. Пример. lim_xŠ∞х²=+∞; lim_xŠ-∞х³=-∞; Замечания:ф-ция y=f(x) при хŠа ил при хŠ∞ может не стремится ни к конечному, ни к бесконечному пределу. 1)y=sinx,xÎR при хŠ∞ y=sinx не имеет предела. 2)ф-ция y=sin1/x, x≠0 при хŠ0 не имеет предела. Опр.ф-ции y=f(x) назыв.ограниченной в нек-ой области изменения х если сущ.число M>0, такое что для всех х из этой области |f(x)|≤M. y=sinx-ограничена, т.к. |sinx|≤1=M. Опр:ф-ция y=f(x) назыв.ограниченной при хŠа если существуют окрестность с центром в точке А, в кот-ой ф-ция f(x) явл.ограниченной. Опр.ф-ция y=f(x) назыв.ограниченной при хŠ∞, если сущ.число N>0, такое что для всех |х|>N ф-ция ограничена. Теорема: если lim_хŠaf(x)=b, где b-конечное число, то f(x) ограничена при хŠа. Док-во.из равенства lim_хŠaf(x)=b=>для любого e>0 сущ.δ>0, такое что для всех х, удовлетворяющих нер-ву 0<|х-а|<δ будет выполняться нер-во |f(x)-b|<e,т.е. в заданной δ окрестности точки а. |f(x)|-|b|≤|f(x)-b|<e; |f(x)|-|b|≤e; |f(x)|<e+|b|=>ф-ция f(х) ограничена в δ окрестности точки а. Замечание:из определения ограниченной ф-ции следует, что если ф-ция f(x) явл.б.б. (т.е.если lim_xŠaf(x)=∞ или lim_xŠ∞f(x)=∞), то она не является ограниченной. Обратное не верно: неограниченная ф-ция может и не быть б.б. Пример.y=xsinx,xÎR-неограниченная,т.к. для любого М>0 найдётся х |хsinx|>M,но эта ф-ция не явл.б.б.,т.к.y=0 при х=0,p,2p…

№42. Теорема о разности между переменной величиной и её пределом.

Опр: число а назыв.пределом переменной величины х если для любого сколь угодно малого положительного числа e можно указать такое значение переменной х, начиная с которого все последующие знач.переменной будут удовлетворять след.нер-ву: |х-а|<e;-e<x-a<e;a-e<x<a+e а=limх при хŠа. Пример:х₁=1+1;х₂=1+¹/₂;х₃=1+¹/₃;……;х_n=1+¹/_n… Докажем пользуясь опр.,что lim_x→∞x_n=1: Рассм. |x_n-1|<e;|1+¹/_n-1|<e;¹/_n<e;n>¹/_e.=>,что все члены последовательности с номерами большими чем ¹/_e будут удовлетворять след.нер-ву: |x_n-1|<e.ч.т.д.

Замечания:1)очевидно, что предел постоянной величины=самой постоянной,т.е. limc=c,где c=const. Действит.возьмём -e>0 и рассм. |х-с|=|с-с|=0<e,для -e>0. 2)переменная величина не может иметь двух различных пределов. Действит-но limx=a и limx=b,a≠b.пусть для определённости a<b,тогда согласно определению если limx=a и limx=b,то сущ.знач.х, начиная с кот-ого все послед.знач.удовлетворяют нер-ву. limx=a и limx=b; |x-а|<e и |x-b|<e, а это невозможно если взять e<(b-a)/2(см.рис.2). …,если y переменой величины сущ.,то этот предел единственный. Говорят,что переменная хŠ∞ если для каждого наперёд заданного положит-но числа М сущ.такое знач.х, начиная с кот-ого все послед.знач.х удовлетворяют нер-ву |х|>M.если переменная хŠ∞, то её назыв.бесконечно большой переменной величиной (б.м.в.).Пример:х₁=-1,х₂=2,х₃=-3…х_n=(-1)ⁿ*n-эта переменная величина будет бесконечно малойсм.(рис.3).Говорят,что переменная величина хŠ+∞,если для -М>0 все послед.знач.х удовлетворяют нер-ву. Пример: х₁=1,х₂=2…х_n=n…(см.рис.4.).Говорят,что переменная хŠ-∞,если для любого M>0 все послед.знач.х начиная с нек-ого удовл.нер-ву.x<-M(см.рис.5). Пример. х₁=-1,х₂=-2,х₃=-3…х_n=-n…

№43. предел суммы, разности, произведения, частного.

Доказательство

Рассмотрим односторонние пределы 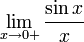и 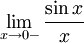и докажем, что они равны 1.

Пусть 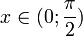. Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

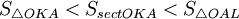(1)

(где S_sectOKA — площадь сектора OKA)

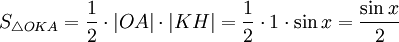
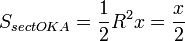
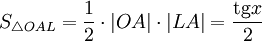
(из 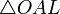: | LA | = tgx)

Подставляя в (1), получим:

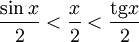
Так как при :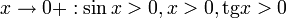

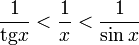
Умножаем на sinx:

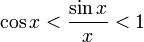
Перейдём к пределу:

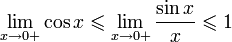
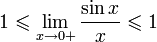
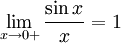
Варианты первого замечательного предела

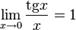
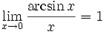
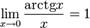
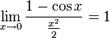
№47. Второй замечательный предел.

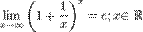
Пусть 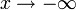. Сделаем подстановку − x = t, тогда

.

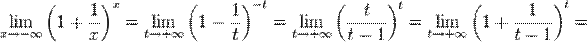
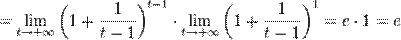Из двух этих случаев вытекает, что 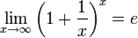для вещественного x.

Варианты второго замечательного.

1. 
2. 
3. 
4. 
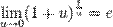
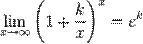
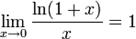
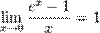
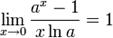5. для ,
6. 

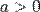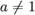
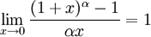
№48. Сравнение бесконечно малых.

Пусть lim_xŠaα(x)=0, lim_xŠaβ(x)=0. Найдём lim_xŠa^α(x)/_β(x)=[⁰/₀].

1)опр.1.если предел отношения ^α(x)/_β(x) при xŠa равен С, где С=const отличное от нуля то α(x) и β(x) называются бесконечно малыми одного и того же порядка, т.е. lim_xŠa^α(x)/_β(x)=С, С=сonst, С=0;

2)опр.2. Если предел α(х), β(x) при xŠa=0, то α(х) называется бесконечно малой величиной более высокого порядка или β(x), т.е. lim_xŠa^α(x)/_β(x)=0; α(х)=0 (β(х)). α(х)–есть 0-мало от β(x).

3)опр.3. Если lim_xŠa^α(x)/_β(x)=1=>назыв. эквивалентными бесконечно малыми.=> α(х)~β(x). 4)опр.4. Если lim_xŠa^α(x)/[β(x)]^k=const, где С≠0, то α(х) называется бесконечно малой величиной порядка k относительно β(x).

5)Опр.5. Если lim_xŠa^α(x)/_β(x)-не сущ., то α(х) и β(x) называются несравнимыми б.м.в. Теорема 1: Если α(х) и β(x) –эквивалентные б.м.в. при xŠa, то α–β – есть б.м.в. более высокого порядка чем α или β. lim_xŠa^α-β/_α=0; lim_xŠa^α-β/_β=0. Док-во: пусть α(х) эквивалентно β(x) при xŠa=> lim_xŠa^α(x)/_β(x)=1= ^β(x)/_α(x)=1. Рассм. lim_xŠa^α-β/_α= lim_xŠa(1-^β/_α)=1-lim_xŠa ^β/_α=1-1=0=> α–β=0(α). lim_xŠa ^α-β/_β= lim_xŠa(^α/_β-1)= lim_xŠa^α/_β -1=1-1=0=> α–β=0(β).

Теорема 2,обратной 1. Если разность 2-х б.м.в. α(х)-β(x) при xŠa есть б.м.в. и относит. α(х) и β(x), то α и β – есть эквивалентные б.м.в.,т.е. α(х)-β(x)=0 (α(х))=>α(х)~β(x) и α(х)-β(x)=0 (β(х))=>α(х)~β(x). Док-во: т.к. α(х)-β(x)=0(α(х))=> lim_xŠa(^{α(х)-β(х)}/_α(х))=0=> lim_xŠa(1-^β/_α)=0=> lim_xŠa 1- lim_xŠa^β/_α=0 или lim_xŠa^β/_α=1=>α(х)~β(x). α(х)-β(x)=0 (β(х))= lim_xŠa ^α-β/_β=0=> lim_xŠa (^α/_β-1)=0=> lim_xŠa ^α/_β=1=> α(х)~β(x).

№57. Односторонние пределы

Если у любой сходящейся к точке x₀ последовательности {x_n} все ее элементы меньше x₀, а соответствующая последовательность 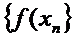сходится к A₁, то число A₁ называется левым пределом функции f(x).

Обозначение: .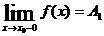

Если у любой сходящейся к 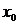последовательности 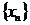все ее элементы больше 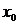, а соответствующая последовательность 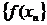сходится к 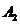, то число 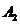называется правым пределом функции f(x):

Обозначение: .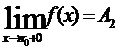

№58. Три определения непрерывности ф-ции в точке. Классификация точек разрыва.

Ф-ция у=f(х) назыв.непрерывной на интервале (а;b) если она непрерывна в каждой точке этого интервала. Опр. lim_xŠa+0f(x)=f(a), то ф-ция f(х) называется непрерывной в точке а справа. lim_xŠb-0f(x)=f(b), то ф-ция f(х) называется непрерывной в точке b слева. Опр: ф-ция у=f(х) назыв. непр.на отрезке [a;b] если она непрерывна в каждой точке интервала (а;b), непрерывна справа в точке а и непрерывна слева в точке b. Если в какой-то точке х_о для ф-ции у=f(х) не выполняется хотя бы одно условие непрерывности, то ф-ция у=f(х) разрывна в точке х_о. В этом случае точка х_о называется точкой разрыва для ф-ции у=f(х). Существуют три вида точек разрыва.

1)если существует предел lim_xŠхоf(x)=a, но он не равен значению ф-ции в точке х_о, тогда точка х_о – точка устранимого разрыва.

2)если существует предел ф-ции f(x) при х стремящемся от х_о справа,т.е. lim_xŠхо+0f(x)=f(x_o+0). Существует предел ф-ции f(x) при хŠх_о слева, т.е. lim_xŠхо-0f(x)=f(x_o-0), но они не равны между собой f(x_o+0)≠f(x_o-0), то х_о-точка разрыва 1-го рода (точка скачка). Разность f(x_o+0)-f(x_o-0)-величина скачка в точке х_о, т.е. всегда от правостороннего отнимается левосторонний.

3)если хотя бы один из односторонних пределов в точке х_о не сущ. или равен ∞, то точка х_о называется точкой разрыва второго рода. $ lim_xŠхо-0f(x)=a; lim_xŠхо+0f(x)=+∞. Примеры 3)-_{(продолжение)} у=^х/_|х|, х≠0 lim_хŠ0+ ^х/_|х|= lim_хŠ0 ^х/_х=1 и lim_хŠ0- ^х/_|х|= lim_хŠ0 ^х/_-х=-1 => по определению, что точка х=0 – точка разрыва 1-го рода.

№59. Непрерывность суммы, произведения и частного непрерывных ф-ций. Непрерывность сложной ф-ции.

Пусть ф-ция у=f(x) задана в некоторой точке хо и некоторой окрестности с центром в точке хо. (см.рис.1.). Придадим аргументу хо некоторое приращение ∆х, т.е. хо+∆х=х, тогда значение ф-ции также изменится. Пусть f(хо)=у. Положим f(хо+∆х)=уо+∆у, тогда ∆у=f(хо+∆х)- f(хо)-приращение ф-ции в точке хо. Опр.:ф-ция у=f(x) называется непрерывной в точке хо, если бесконечно малому приращению аргумента точке хо соответствует бесконечно малое приращение ф-ции в этой точки,т.е. lim∆х0∆у=0 или lim∆х0(f(хо+∆х)- f(хо))=0 или lim∆х0 f(хо+∆х)= f(хо) или limххо f(x)=f(хо) (*),где limххо x=хо. из (*)=>limххо f(x)=f(limххох), т.е. для того чтобы найти предел непрерывной ф-ции в точке хо достаточно подставить в выражение ф-ции вместо аргумента х его значение хо. Пример: докажем: ф-ция у=х2 – непрерывна для любого хо. 1)Возьмём хо. хо=хо+∆х, тогда ф-ция получит приращение ∆у=у(хо+∆х)- у(хо)=(хо+∆х)2-хо2= хо2+2хо*∆х+(∆х)2-хо2=2хо*∆х+(∆х)2. lim∆х0 ∆у= lim∆х0(2хо*∆х+(∆х)2)=0, а это по опр.и означает, что ф-ция y=х2 –непрерывна в любой точке хо.

2)у=sinx, хоR. ∆у=sin(хо+∆х)-sinхо=2sin∆х/2*cos(хо+∆х/2); lim∆х0∆у= lim∆х02sin∆х/2*cos(хо+∆х/2)=0. Аналогично рассматривая