Достаточные признаки существования экстремума (доказать одну из теорем).

Теорема (первое достаточное условие экстремума).Пусть в точке функция непрерывна, а производная при переходе через точку меняет знак. Тогда – точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «–» на «+».

Доказательство. Пусть при и при .

По теореме Лагранжа , где .Тогда если , то ; поэтому и , следовательно, , или . Если же , то ; поэтому и , следовательно, или .

Таким образом доказано, что в любых точках вблизи , т.е. – точка максимума функции .

Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.

Если при переходе через точку производная не меняет знак, то в точке экстремума нет.

Теорема (второе достаточное условие экстремума). Пусть в точке производная дважды дифференцируемой функции равна 0 ( ), а ее вторая производная в этой точке отлична от нуля ( ) и непрерывна в некоторой окрестности точки . Тогда – точка экстремума ; при это точка минимума, а при это точка максимума.

Алгоритм нахождения экстремумов функции с помощью первого достаточного условия экстремума.

1. Найти производную.

2. Найти критические точки функции.

3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов.

4. Найти экстремальные значения функции.

Алгоритм нахождения экстремумов функции с помощью второго достаточного условия экстремума.

1. Найти производную .

2. Найти вторую производную .

3. Найти те точки, в которых .

4. В этих точках определить знак .

5. Сделать вывод о существовании и характере экстремумов.

6. Найти экстремальные значения функции.

Пример. Рассмотрим . Найдем . Далее, при и при . Исследуем критические точки с помощью первого достаточного условия экстремума. Имеем, что при и при , и при . В точках и производная меняет свой знак: при с «+» на «–» и при с «–» на «+». Это значит, что в точке функция имеет максимум, а точке – минимум; . Для сравнения исследуем критические точки с помощью второго достаточного условия экстремума. Найдем вторую производную . Имеем: , а это значит, что в точке функция имеет максимум, а точке – минимум.

Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Различают вертикальные (рис. 6.6 а), горизонтальные (рис. 6.6 б) и наклонные (рис. 6.6 в) асимптоты.

На рис. 6.6а изображена вертикальная асимптота.

На рис 6.6б – горизонтальная асимптота.

На рис. 6.6в – наклонная асимптота.

Теорема 1. В точках вертикальных асимптот (например, ) функция 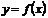терпит разрыв, ее предел слева и справа от точки равен :

и (или) .

Теорема 2. Пусть функция определена при достаточно больших 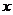и существуют конечные пределы

и .

Тогда прямая является наклонной асимптотой графика функции .

Теорема 3.Пусть функция определена при достаточно больших 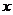и существует предел функции . Тогда прямая есть горизонтальная асимптота графика функции .

Горизонтальная асимптота является частным случаем наклонной асимптоты, когда . Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Пример.Найти асимптоты графика функции .

Решение. В точке 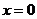функция не определена, найдем пределы функции слева и справа от точки :

; .

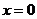Следовательно, 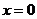- вертикальная асимптота.

Найдем наклонную асимптоту: ; . Таким образом, - наклонная асимптота (рис. 6.7).

Общая схема исследования функций и построения их графиков. Пример.

Общая схема исследования функции и построения ее графика.

1. Найти область определения .

2. Исследовать функцию на четность – нечетность.

3. Найти вертикальные асимптоты и точки разрыва (если есть).

4. Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).

5. Найти экстремумы и интервалы монотонности функции.

6. Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.

7. Схематично построить график.

Подробная схема исследования функции и построения графика.

1. Найти область определения .

a. Если у есть знаменатель, он не должен обращаться в 0.

b. Подкоренное выражение корня четной степени должно быть неотрицательным (больше либо равно нулю).

c. Подлогарифмическое выражение должно быть положительным.

2. Исследовать функцию на четность – нечетность.

a. Если , то функция четная.

b. Если , то функция нечетная.

c. Если не выполнено ни , ни , то – функция общего вида.

3. Найти вертикальные асимптоты и точки разрыва (если есть).

a. Вертикальная асимптота может возникнуть только на границе области определения функции.

b. Если ( или ), то – вертикальная асимптота графика .

4. Исследовать поведение функции в бесконечности; найти горизонтальные и наклонные асимптоты (если есть).

a. Если , то – горизонтальная асимптота графика .

b. Если и , то прямая является наклонной асимптотой графика .

c. Если пределы, указанные в п. a, b, существуют только при одностороннем стремлении к бесконечности ( или ), то полученные асимптоты будут односторонними: левосторонними при и правосторонними при .

5. Найти экстремумы и интервалы монотонности функции.

a. Найти производную .

b. Найти критические точки (те точки, где или где не существует).

c. На числовой оси отметить область определения и ее критические точки.

d. На каждом из полученных числовых интервалов определить знак производной .

e. По знакам производной сделать вывод о наличии экстремумов у и их типе.

f. Найти экстремальные значения .

g. По знакам производной сделать вывод о возрастании и убывании .

6. Найти точки пересечения графика с осями координат и, если это нужно для схематического построения графика, найти дополнительные точки.

a. Для того, чтобы найти точки пересечения графика с осью , надо решить уравнение . Точки , где – нули , будут точками пересечения графика с осью .

b. Точка пересечения графика с осью имеет вид . Она существует, только если точка входит в область определения функции .

8. Схематично построить график.

a. Построить систему координат и асимптоты.

b. Отметить экстремальные точки.

c. Отметить точки пересечения графика с осями координат.

d. Схематично построить график так, чтобы он проходил через отмеченные точки и приближался к асимптотам.

Пример. Исследовать функцию и схематично построить ее график.

1. .

2. – функция общего вида.

3. Поскольку и , то прямые и являются вертикальными асимптотами; точки и являются точками разрыва.

4. Поскольку , прямая – горизонтальная асимптота графика .

5. ; при . На числовой оси отмечаем точки , (не входят в область определения ) и (критическая точка ). На каждом из полученных числовых интервалов определяем знак производной : при , при , при , при . Делаем выводы: – точка максимума (в этой точке производная меняет знак с «+» на «–»), ; при и при возрастает; при и при убывает.

6. Точка пересечения графика с осью : . Точка пересечения графика с осью отсутствует, так как точка не входит в область определения функции .

7. См. рис. 7.

Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия.

Основные понятия. Частные производные

Определение. Пусть имеется 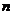переменных величин и каждому набору их значений из некоторого множества соответствует одно вполне определенное значение переменной величины из множества . тогда говорят, что задана функция нескольких переменных .

Переменные называются независимыми переменными или аргументами, - зависимая переменная. Множество называется областью определения функции, множество - областью значений функции.

Функцию двух переменных будем обозначать как .

Определение. Графиком функции двух переменных называется множество точек трехмерного пространства ( ), аппликата которых связана с абсциссой 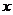и ординатой функциональным соотношением . График представляет собой некоторую поверхность в трехмерном пространстве.