Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.
Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.
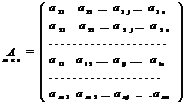 Определение. Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов.
Определение. Матрицей размера называется прямоугольная таблица, содержащая m строк и n столбцов.
Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты.
Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца:
Виды матриц:
1) Матрица-строка: ;
2) Матрица-столбец: ; 3) Нулевая матрица: ;
4) Квадратная матрица – если (например n = 2): ;
5) Диагональная матрица (напр. 3-го порядка, где любые числа ): ;
6) Единичная матрица (например, 3-го порядка) 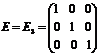
Операции над матрицами
1. Умножение матрицы на число.
Произведением матрицы A на числоназывается матрица,элементы которойдля
Пример.Вычислить , если . Р е ш е н и е: .
Если  , то
, то  (нулевая матрица того же размера).
(нулевая матрица того же размера).
2. Сложение матриц.
Суммой матриц 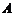 и
и 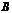 одинакового размера
одинакового размера 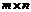 называется матрица
называется матрица 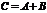 , элементы которой
, элементы которой 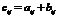 для
для
Пример. Вычислить С = А + В, если . Р е ш е н и е: .
3. Вычитание матриц.
Разность матриц одинакового размера определяется как 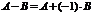 .
.
4. Умножение матриц.
Умножение матрицы 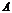 на матрицу
на матрицу 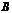 определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц
определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц 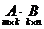 называется матрица
называется матрица 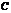 , каждый элемент которой
, каждый элемент которой 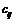 равен сумме произведений элементов
равен сумме произведений элементов 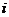 -ой строки матрицы
-ой строки матрицы 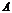 на соответствующие элементы
на соответствующие элементы 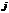 -го столбца матрицы
-го столбца матрицы 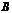 :
:
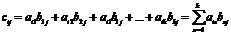 , где
, где
Пример.Вычислить произведение матриц 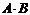 , где
, где 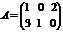 ,
, 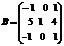 .
.
Р е ш е н и е.
Найдем размер матрицы произведения 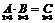 , следовательно, умножение возможно.
, следовательно, умножение возможно.
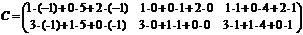 =
= 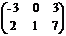 .
.
Свойства операций сложения и умножения матриц
1) 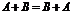 . 5)
. 5) 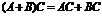 .
.
2) 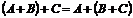 . 6)
. 6) 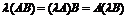 .
.
3) 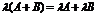 . 7)
. 7) 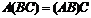 .
.
4) 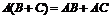 .
.
8) 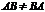 (в общем случае). Кроме того, если
(в общем случае). Кроме того, если 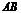 существует, то
существует, то 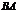 может вообще не существовать.
может вообще не существовать.
9) 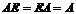
 , где
, где 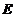 - единичная квадратная матрица.
- единичная квадратная матрица.
10) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если 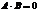 , то не следует, что
, то не следует, что 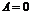 или
или 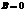 .
.
Пример. 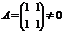 ,
, 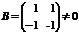 , но
, но 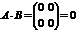 .
.
5. Возведение в степень.
Целой положительной степенью 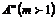 квадратной матрицы называют произведениематриц, равных, т.е. .
квадратной матрицы называют произведениематриц, равных, т.е. .
6. Транспонирование матриц.
Транспонирование матрицы есть переход матрицы 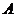 к матрице
к матрице 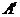 , в которой строки и столбцы поменялись местами с сохранением порядка.
, в которой строки и столбцы поменялись местами с сохранением порядка.
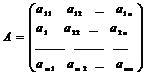 ,
, 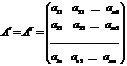 ,
,
т.е. если 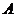 имеет размер
имеет размер 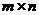 , то
, то 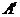 имеет размер
имеет размер 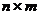 .
.
Свойства операции транспонирования.
1) 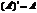 . 3)
. 3) 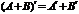 .
.
2) 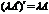 . 4)
. 4) 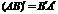 .
.
2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца.
Определители и их свойства
Понятие определителя - число, характеризующее квадратную матрицу, необходимо для решения систем линейных алгебраических уравнений.
Определитель матрицы обозначают , 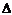 ,
, 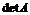 .
.
1) Определителем матицы 1-го порядка 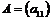 , называется элемент : ;
, называется элемент : ;
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
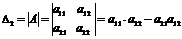 . Произведения называются членами определителя 2-го порядка.
. Произведения называются членами определителя 2-го порядка.
Пример.Вычислить определитель матрицы 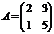 . Р е ш е н и е.
. Р е ш е н и е. 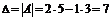 .
.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
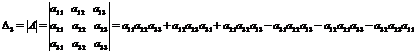 .
.
Данная формула получила название правила треугольников или правило Сарруса.
При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:
 |
Пример. Вычислить определитель
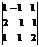 . Р е ш е н и е.
. Р е ш е н и е. 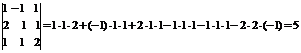 .
. 4) Определитель квадратной матрицы 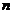 -го порядка (определитель
-го порядка (определитель  -го порядка).
-го порядка).
Рассмотрим квадратную матрицу n-го порядка. Зачеркнем элемент матрицы, стоящий на пересечении 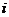 -й строки и
-й строки и 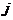 -го столбца. В результате получается матрица порядка
-го столбца. В результате получается матрица порядка 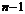 . Пусть дана матрица n-го порядка:
. Пусть дана матрица n-го порядка:
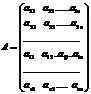 .
.
Минором 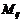 элемента
элемента 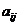 матрицы n-го порядка называется определитель матрицы
матрицы n-го порядка называется определитель матрицы 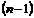 -го порядка, полученной из матрицы
-го порядка, полученной из матрицы 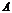 вычеркиванием
вычеркиванием 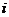 -й строки и
-й строки и 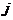 -го столбца.
-го столбца.

 Например минором матрицы 3-го порядка будет:
Например минором матрицы 3-го порядка будет:
Определение. Алгебраическим дополнением 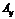 элемента
элемента 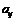 матрицы
матрицы 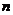 -го порядка называется минор, взятый со знаком
-го порядка называется минор, взятый со знаком 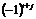 :
:
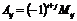 .
.
Пример. Найти алгебраические дополнения всех элементов матрицы
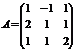 .
.
Р е ш е н и е:
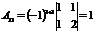 , , | 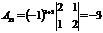 , , | 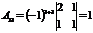 , , | 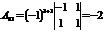 | 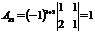 | 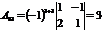 |
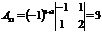 , , | 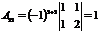 , , | 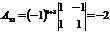 , , |
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
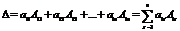 (разложение по элементам
(разложение по элементам 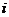 -й строки;
-й строки; 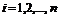 ).
).
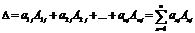
(разложение по элементам 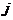 -го столбца;
-го столбца; 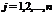 ).
).
Пример.Вычислить определитель 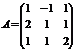 разложением по элементам
разложением по элементам
а) 1-й строки; б) 1-го столбца.
Р е ш е н и е. а) 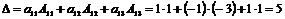 , б)
, б) 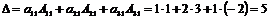 .
.
Свойства определителей
1.Если какая-либо строка (столбца) матрицы состоит из одних нулей, то ее определитель равен 0.
2.Если все элементы какой-либо строки (столбца) матрицы умножить на число ,то ее определитель умножится на это число .
Замечание. За знак определителя можно выносить общий множитель любой строки (столбца) в отличие от матрицы, за знак которой можно выносить общий множитель всех элементов.
3.При транспонировании матрицы ее определитель не изменяется: 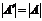 .
.
4.При перестановки двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.
5.Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.
6.Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
7.Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.
8.Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
9.Сумма произведений произвольных чисел 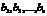 на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа
на алгебраические дополнения любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа 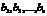 .
.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: 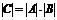 , где
, где 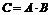 , а
, а 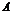 и
и 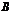 - матрицы
- матрицы 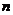 -го порядка.
-го порядка.
Перечисленные свойства определителей позволяют существенно упростить их вычисления для определителей высоких порядков. При этом с помощью свойств 1-9 желательно преобразовать исходную матрицу таким образом, чтобы она имела строку (столбец), содержащую как можно больше нулей, а потом вычислить определитель, разложенный по этой строке (столбцу).
Обратная матрица
Для каждого числа 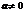 существует обратное число
существует обратное число 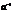 такое, что произведение
такое, что произведение 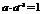 . Для квадратных матриц тоже вводится аналогичное понятие.
. Для квадратных матриц тоже вводится аналогичное понятие.
Определение. Матрица 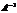 называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
называется обратной по отношению к квадратной матрице , если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица:
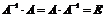 .
.
Только квадратная матрица может иметь обратную, однако не каждая квадратная матрица имеет обратную.
Определение. Матрица является невырожденной (неособенной), если 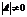 , в противном случае при
, в противном случае при 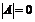 матрица
матрица 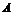 называется вырожденной (особенной).
называется вырожденной (особенной).
Теорема (необходимое и достаточное условие существования обратной матрицы). Обратная матрицасуществует (и единственна) тогда и только тогда, когда исходная матрица является невырожденной (неособенной) и вычисляется по формуле
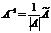 ,
,
где 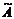 - присоединенная матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы, т.е.
- присоединенная матрица, состоящая из алгебраических дополнений элементов транспонированной матрицы, т.е. 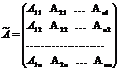 .
.
Необходимость. Пусть матрица имеет обратную , т.е. . По свойству 10 определителей имеем: , т.е. и .
Достаточность. Пусть . Рассмотрим квадратную матрицу n-го порядка , называемую присоединенной, элементы которой являются алгебраическими дополнениями элементов матрицы , транспонированной к . Тогда элементы произведения матриц определяются по правилу умножения матриц. Поэтому матрица В является диагональной, элементы ее главной диагонали равны определителю исходной матрицы. А произведение на равно той же матрице В: .
Единственность обратной матрицы. Предположим, что существуют еще матрицы и такие, что и , где матрица получена по формуле 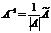 и выполняются равенства и . Тогда, умножая на слева первое из них, получаем: , откуда , т.е. . Аналогично, умножая второе равенство на справа, получаем . Единственность доказана.
и выполняются равенства и . Тогда, умножая на слева первое из них, получаем: , откуда , т.е. . Аналогично, умножая второе равенство на справа, получаем . Единственность доказана.
Пример. Решить систему уравнений по формулам Крамера
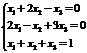
Р е ш е н и е. Определитель матрицы системы 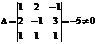 . Следовательно, система имеет единственное решение. Вычислим
. Следовательно, система имеет единственное решение. Вычислим 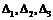 , полученные из
, полученные из 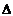 заменой соответственно первого, второго, третьего столбцов столбцом свободных членов:
заменой соответственно первого, второго, третьего столбцов столбцом свободных членов:
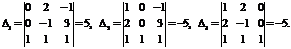
По формулам Крамера:
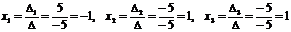 .
.
5. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.
Метод Гаусса - метод последовательного исключения переменных.
Метод Гаусса заключается в том, что с помощью элементарных преобразований строк и перестановок столбцов система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей их коэффициентов 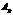 , получаемой приписыванием к матрице
, получаемой приписыванием к матрице 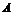 столбца свободных членов
столбца свободных членов 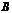 :
:
 .
.
Следует отметить, что методом Гаусса можно решить любую систему уравнений вида  .
.
Пример. Методом Гаусса решить систему:
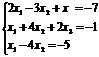
Выпишем расширенную матрицу системы.
Шаг 1. Поменяем местами первую и вторую строки, чтобы 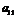 стал равным 1.
стал равным 1.
Шаг 2.Умножим элементы первой строки на (–2) и (–1) и прибавим их к элементам второй и третьей строк, чтобы под элементом 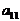 в первом столбце образовались нули.
в первом столбце образовались нули.
Шаг 3. Умножим элементы третьей строки на (–0,5).
Шаг 4. Поменяем местами вторую и третью строки.
Шаг 5.Поменяем местами второй и третий столбец. (Шаги 3, 4, 5 приведены с тем, чтобы 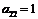 ).
).
Шаг 6. Элементы второй строки умножим на 3 и прибавим их к элементам третьей строки, тогда под элементом 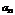 появится нуль.
появится нуль.
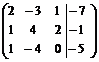 (называется расширенная матрица системы)
(называется расширенная матрица системы) 
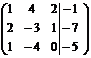

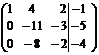

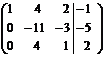

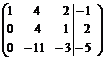

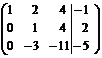

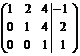 .
.
Расширенная матрица приведена к треугольному виду. Соответствующая ей система имеет вид:
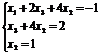
Из последнего уравнения 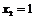 ; из второго
; из второго 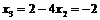 ; из первого
; из первого 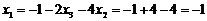 .
.
Таким образом, 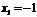 ,
, 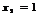 ,
, 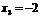 .
.
6. Решение систем п линейных уравнений с п переменными с помощью обратной матрицы (вывод формулы Х=А –1В).
Для получения решения системы  при
при 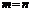 в общем виде предположим, что квадратная матрица системы
в общем виде предположим, что квадратная матрица системы 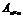 невырожденная, т.е. ее определитель
невырожденная, т.е. ее определитель 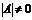 . В этом случае существует обратная матрица
. В этом случае существует обратная матрица 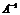 .
.
Метод обратной матрицы.
Запишем систему в матричной форме:
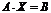 , где
, где
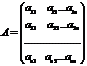 - матрица коэффициентов при переменных,
- матрица коэффициентов при переменных,
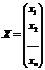 - матрица-столбец переменных;
- матрица-столбец переменных; 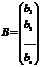 - матрица столбец свободных членов.
- матрица столбец свободных членов.
Умножим слева обе части равенства на матрицу 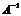 :
:
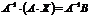 ;
;
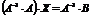 ;
;
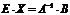 ;
;
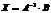 .
.
Таким образом, решение системы в матричном виде 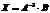 .
.
Пример. Решить систему уравнений методом обратной матрицы. 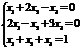
Р е ш е н и е: Обозначим 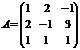 ;
; 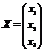 ;
; 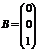 .
.
Тогда в матричной форме система имеет вид: 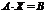 . Определитель матрицы
. Определитель матрицы 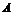
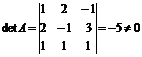 , т.е. обратная матрица
, т.е. обратная матрица 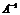 существует:
существует: 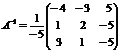 .
.
Определим 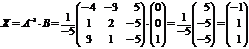 ,
,
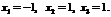
Существенным недостатком решения систем  линейных уравнений с
линейных уравнений с 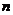 переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождения обратной матрицы.
переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождения обратной матрицы.
7. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).
Теорема Крамера. Пусть - определитель матрицы системы, а - определитель матрицы, получаемой из матрицы заменой -го столбца столбцом свободных членов. Тогда, если, то система имеет единственное решение, определяемое по формулам:
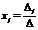 , (
, ( 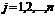 ).
).
В соответствии с обратной матрицей , где - матрица, присоединенная к матрице . Т.к. элементы матрицы есть алгебраические дополнения элементов матрицы , транспонированной к , то запишем равенство 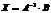 в развернутой форме:
в развернутой форме:
.
Учитывая, что , получим после умножения матриц:
, откуда следует, что для любого .
На основании свойства 9 определителей , где - определитель матрицы, полученной из матрицы заменой -го столбца столбцом свободных членов. Следовательно 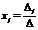 .
.
Решение системы 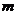 линейных уравнений с
линейных уравнений с 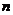 неизвестными
неизвестными
Рассмотрим систему 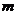 линейных уравнений с
линейных уравнений с 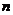 неизвестными.
неизвестными.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы: 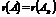 .
.
Для совместных систем линейных уравнений верны следующие теоремы:
Теорема 1. Если ранг матрицы совместной системы равен числу переменных, т.е. 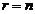 , то система имеет единственное решение.
, то система имеет единственное решение.
Теорема 2. Если ранг матрицы совместной системы меньше числа переменных, т.е. 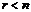 , то система является неопределенной и имеет бесконечное множество решений.
, то система является неопределенной и имеет бесконечное множество решений.
Определение.Базисным минором матрицы называется любой ненулевой минор, порядок которого равен рангу матрицы.
Определение. Те 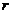 неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные
неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные 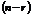 неизвестных называются свободными (или неосновными).
неизвестных называются свободными (или неосновными).
Решить систему уравнений в случае 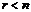 - это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все
- это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все 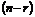 свободные переменные равны нулю, то решение системы называется базисным.
свободные переменные равны нулю, то решение системы называется базисным.
Пример. Решить систему методом Гаусса: 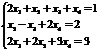
Р е ш е н и е. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам третьей строки элементы первой строки, умноженные на –1. А затем элементы второй строки умножим на –1 и прибавим к элементам третьей строки:
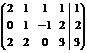

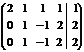

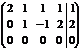 .
.
Расширенная матрица приведена к ступенчатому виду.
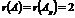 . Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем
. Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем 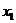 и
и 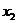 (т.к. определитель, составленный из их коэффициентов не равен нулю
(т.к. определитель, составленный из их коэффициентов не равен нулю 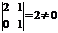 ), тогда
), тогда 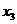 и
и 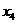 - свободные неизвестные.
- свободные неизвестные.
Выразим базисные переменные через свободные.
Из второй строки полученной матрицы выразим переменную 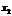 :
:
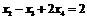 ,
, 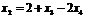 .
.
Из первой строки выразим 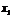 :
: 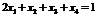 ,
,
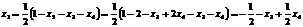 .
.
Общее решение системы уравнений: 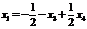 ,
, 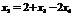 .
.
8. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.
Основные свойства функций
1) Четность и нечетность. Функция называется четной, если для любых значений из области определения и нечетной, если. В противном случае функция называется функцией общего вида.
Пример.
а) Функция 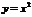 - четная (рис.3.3 а). т.к ; б) Функция - четная (рис.3.3 а). т.к ; б) Функция 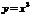 - нечетная (рис.3.3 б). ; в) Функция - нечетная (рис.3.3 б). ; в) Функция 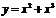 - общего вида (рис.3.3 в). . - общего вида (рис.3.3 в). . |  |
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
2) Монотонность. Функция называется возрастающей (убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Функции возрастающие и убывающие называются монотонными функциями.
Пример.
1) Функция- на интервале 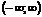 монотонно возрастает (рис.3.4а). 2) Функция монотонно возрастает (рис.3.4а). 2) Функция 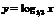 - на интервале - на интервале 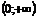 монотонно убывает (рис.3.4 б). монотонно убывает (рис.3.4 б). | 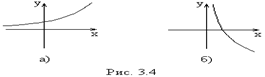 |
3) Ограниченность. Функция называется ограниченной на промежутке , если существует такое положительное число 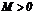 , что
, что 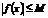 для любого
для любого 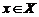 . В противном случает функция называется неограниченной.
. В противном случает функция называется неограниченной.
- ограничена на всей числовой оси, т.к. для любого .
4) Периодичность. Функция 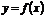 называется периодической с периодом
называется периодической с периодом 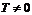 , если для любых из области определения функции
, если для любых из области определения функции 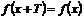 .
.
Пример.
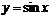 , период , период 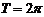 , т.к. для любых , т.к. для любых 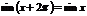 . . |  |
Элементарная функция
Из основных функции новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операции образования сложной функции.
Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Пример.
1) 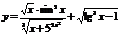 - элементарная функция, т.к число операций сложения, вычитания0 умножения, деления и образования сложной функции конечно.
- элементарная функция, т.к число операций сложения, вычитания0 умножения, деления и образования сложной функции конечно.
2) - неэлементарная функция.
Уравнение пучка прямых
Уравнение прямой в отрезках
Уравнение называется уравнением прямой в отрезках.
Точка пересечения прямых
Если заданы две прямые 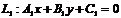 и
и 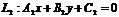 , то координаты точки их пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы:
, то координаты точки их пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы: 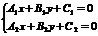 .
.
Если прямые не параллельны, т.е. 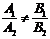 , то решение системы дает единственную точку пересечения прямых.
, то решение системы дает единственную точку пересечения прямых.
Предел функции в точке
Определение.Число 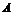 называется пределом функции
называется пределом функции 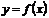 при
при 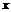 стремящемся к
стремящемся к 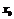 (или в точке
(или в точке 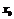 ), если для любого, даже сколько угодно малого положительного числа
), если для любого, даже сколько угодно малого положительного числа 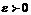 , найдется такое положительное число
, найдется такое положительное число 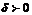 (зависящее от
(зависящее от 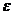 ), что для всех
), что для всех 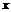 , не равных
, не равных 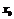 и удовлетворяющих условию
и удовлетворяющих условию 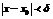 , выполняется неравенство
, выполняется неравенство 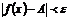 .
.
Это предел функции обозначается: 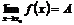 или
или 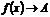 при
при 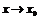 .
.
Бесконечно малые величины
Определение. Функция 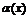 называется бесконечно малой величиной при
называется бесконечно малой величиной при 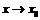 или при
или при 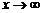 , если ее предел равен нулю:
, если ее предел равен нулю:
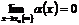 .
.
Бесконечно большие величины
Определение.Функция 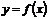 называется бесконечно большой при
называется бесконечно большой при 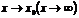 , если ее предел равен бесконечности:
, если ее предел равен бесконечности:
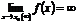 .
.
Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры.
Непрерывность функции
Определение 1. Функция 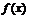 называется непрерывной в точке
называется непрерывной в точке 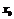 , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям:
1) определена в точке 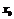 , т.е. существует
, т.е. существует 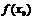 ;
;
2) имеет конечные односторонние пределы функции при 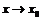 слева и справа;
слева и справа;
3) эти пределы равны значению функции в точке 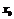 , т.е.
, т.е.
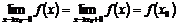 .
.
Пример.Исследовать функции на непрерывность в точке 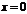 :
:
а) 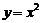 , б)
, б) 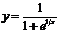 .
.
Решение. а) 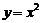 . При
. При 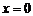 функция определена,
функция определена, 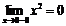 ,
, 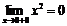 ,
, 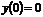 , т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция
, т.е. все три условия непрерывности функции в точке выполнены. Следовательно, функция 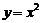 в точке
в точке 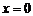 непрерывна.
непрерывна.
б) 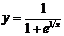 . При
. При 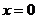 функция не определена;
функция не определена; 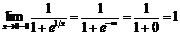 ;
; 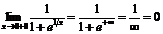 .
.
Т.о. в точке 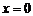 функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
Определение 2. Функция 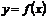 называется непрерывной в точке
называется непрерывной в точке 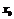 , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
, если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции: 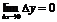 .
.
Определения 1 и 2 равносильны.
Точка 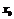 называется точкой разрыва функции
называется точкой разрыва функции 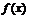 , если эта функция в данной точке не является непрерывной. Различают точки разрыва:
, если эта функция в данной точке не является непрерывной. Различают точки разрыва:
Первого рода – когда существуют конечные односторонние пределы функции слева и справа при 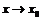 , не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при
, не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при 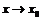 существует, но не равен значению функции в этой точке.
существует, но не равен значению функции в этой точке.
Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.
Точки разрыва функции
Определение. Если в какой-нибудь точке 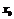 для функции
для функции 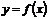 не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.
не выполняется по крайней мере одно из условий непрерывности, то эта точка называется точкой разрыва функции.
Причем: 1) Если существуют конечные односторонние пределы функции, неравные друг другу: 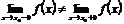 , то точка
, то точка 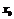 - точка разрыва I рода.
- точка разрыва I рода.
2) Если хотя бы один из односторонних пределов функции 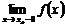 или
или 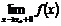 равен бесконечности или не существует, то точка
равен бесконечности или не существует, то точка 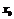 - точка разрыва II рода.
- точка разрыва II рода.
Определение производной
Пусть на некотором промежутке Х определена функция y=f(x). Возьмем любую точку 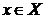 . Зададим аргументу х произвольное приращение ∆х ≠ 0 такое, что точка х+∆х также будет принадлежать
. Зададим аргументу х произвольное приращение ∆х ≠ 0 такое, что точка х+∆х также будет принадлежать
