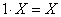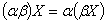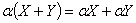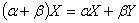Вопрос 7. Решение СЛУ. Метод Крамера, матричный метод, метод Гауса

Метод Крамера

Назовем главным определителем этой системы определитель 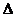, элементами которого являются коэффициенты при неизвестных:

.

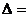
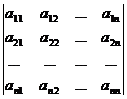Предположим сначала, что 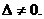Умножим каждое уравнение системы (2.3) на алгебраические дополнения 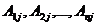элементов j-го столбца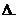

Сложив затем все уравнения, получим:

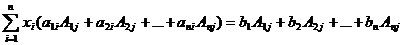. (2.5)

Отметим, что .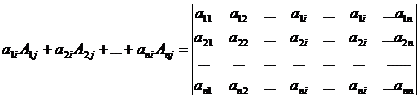

(j-й столбец)

(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при 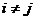и равен 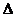при i = j. Правая часть равенства (2.5) представляет собой определитель 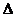, в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель 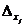. Рассматривая j = 1,2,…,n, получим систему, эквивалентную исходной: 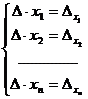(2.6) . Разделив все уравнения на 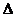, найдем единственное решение: .

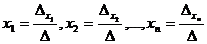Предположим теперь, что 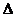=0. Тогда система (2.6) примет вид: .

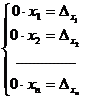В этом случае, если все 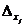=0, система выглядит так: 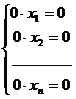и имеет бесконечно много решений. Если же хотя бы один из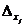 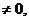система решений не имеет.

Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

1) Если 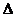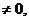система (2.3) имеет единственное решение, определяемое по формулам: .

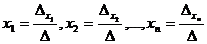2) Если 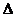= =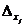0, система имеет бесконечно много решений.

3) Если 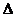=0, а хотя бы один из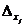 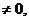система не имеет решений.

Метод Гауса.

Пусть имеется СЛУ:

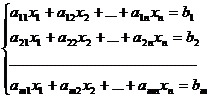
Метод Гауса, заключается в приведении матрицы коэффициэнтов СЛУ к треугольному виду, путем

элементарных преобразований.

Элементарные преобразования:

1)Умножение строки матрицы на число.

2)Добавление к строчке другой строки умноженное на число альфа.

3)Замена строк местами.

Доказательство.

1)Умножаем строку на число Альфа:

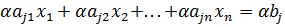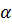, где (альфа) не равна нулю =>решение не меняется.

2)Сумма строк

+

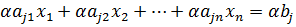
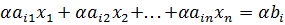
При сложении 2 строк с некоторым коэффициентом если ранее выполнялись тождества для отдельной строки, то и в сумме также будет выполняться равенства. При этом данное преобразование обратимо и не добавляет новых решений.

=>

=>

a a a

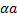b b+ b

+(-

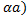
Из тождества aи bполучается b+ 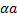, но из тождества а и b+ 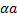можно получить тождества aи b.

Матричный метод.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Метод основан на применении свойств умножения матриц.

Пусть дана система уравнений:

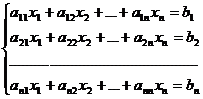
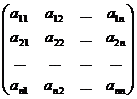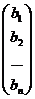Составим матрицы: A= ; B = ; X = .

Систему уравнений можно записать:A×X = B.

Сделаем следующее преобразование: A^-1×A×X = A^-1×B, т.к. А^-1×А = Е, тоЕ×Х = А^-1×В

Х = А^-1×В

Вопрос 8.Однородные СЛУ. Построение фундаментальной системы решений

Однородная Система Уравнений (ОСУ) – называется СЛУ , в которой свободные коэффициенты равны 0.

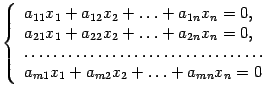
Однородная СЛУ всегда имеет хотя бы одно решение.

Найдем все решения ОСЛУ, методом Гаусса можно привести данную матрицу к треугольной.

Если ранг матрицы равен n, то элементарными преобразованиями из СЛУ можно получить равносильную ей вида:

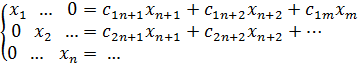
При этом любому набору 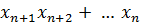можно сопоставить решение СЛУ

Любая линейная комбинация решений ОСЛУ является решением СЛУ.

Количество линейно независимых решений равно m-rangA, где m-число переменных;

если m=rangA, то Фундаментальной Системы Решений не существует.

ФСР: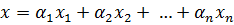

Исследовать однородную систему — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Вопрос 9. Векторы. Основные понятия. Скалярное произведение, его свойства

Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Определение.Длиной (модулем) вектора называется расстояние между началом и концом вектора.

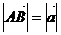
Определение.Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Определение.Векторы называются компланарными, если существует плоскость, которой они параллельны.

Определение.Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.

Определение.Линейными операциями над векторами называется сложение и умножение на число.

Суммой векторов является вектор -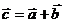

Произведение - 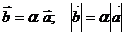, при этом коллинеарен .

Вектор сонаправлен с вектором ( ­­ ), если a> 0.

Вектор противоположно направлен с вектором ( ­¯ ), если a< 0.

Линейным пространством над полем 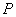(P- Это поле)называется множество 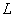, в котором введены операция сложения и операция умножения на числа из поля 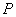. Причем, выполняются следующие аксиомы:

Аксиомы, определяющие операцию сложения.

1. 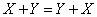, коммутативность

2. 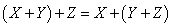, ассоциативность

3. 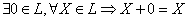, существование нулевого вектора

4. 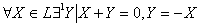(для любого вектора 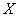из множества 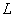существует единственный 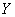такой, что ).

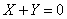Аксиомы, определяющие операцию умножения на числа.

1. 
2. 
3. 
4. 

Скалярным произведениемвекторов и называется число, равное произведению длин этих сторон на косинус угла между ними.

× = ï ïï ïcosj

Свойства скалярного произведения: