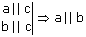Некоторые следствия из аксиом
| Теорема 1. Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна. | 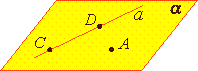 |
| Теорема 2. Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна. | 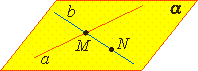 |
Билет 2.1
Арифметическим квадратным корнем из числа а называется неотрицательное число b, квадрат которого равен а:
√а = b ( при a ≥ 0, b ≥ 0, b2 = a).
Пример:
√9 = 3 (9 ≥ 0, 3 ≥ 0, 32 = 9)
При а < 0 выражение √a не имеет смысла.
Пример:
√-25 – невозможно извлечь корень: 52 = 25 и -52 = 25 (а не -25)
При любом а, при котором выражение √a имеет смысл, верно равенство (√a)2 = |а|.
Пример:
(√25)2 = 52 = 25
√-52 = √25 = 5
Свойства арифметического квадратного корня:
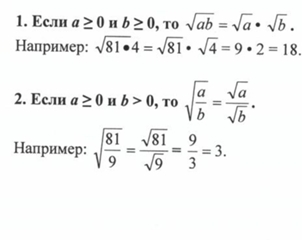 3.(√a)n = √an (приa ≥ 0)
3.(√a)n = √an (приa ≥ 0)
Например:
(√16)3 = √163 = √4096 = 64
√163 = (√16)3 = 43 = 64
Арифметические корниn-й степени.
4√81 = 3 (так как 34 = 81)
Читается так: корень четвертой степени из 81 равен 3.
Преобразование выражений с квадратными корнями. 
2.2
Прямая параллельная плоскости.
Прямая параллельна плоскости, когда она параллельна прямой, лежащей в этой плоскости.
Если требуется провести прямую параллельно данной плоскости, то сначала надо провести в плоскости какую-либо прямую, а затем провести прямую, ей параллельную, которая будет параллельна данной плоскости.
В плоскости можно провести неограниченное число прямых линий, следовательно, можно провести неограниченное количество и прямых, параллельных плоскости.
Определение: прямая параллельна плоскости, если она параллельна прямой, принадлежащей данной плоскости.
Определение 2.3.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Если прямая a параллельна плоскости α, то пишут a || α.
Теорема 2.4. Признак параллельности прямой и плоскости.
Если прямая вне плоскости параллельна какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
Теорема 2.5. Теорема о следе.
Если плоскость β проходит через прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a.
Определение 2.4.
Прямую b иногда называют следом плоскости β на плоскости α.
Билет 3.1
Арифметическим корнем n-й степени из числа а называют неотрицательное число , n-я
степень которого равна а.
Обозначается арифметический корень n-й степени из числа а
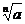 ,
,
где n- показатель корня,
а- подкоренное выражение.
Знак 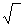 называют еще радикалом.
называют еще радикалом.
Арифметический корень второй степени называется корнем квадратным и обозначается √,
арифметический корень третьей степени называется кубическим корнем о обозначается 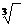
Например :
а) 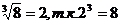 и 2≥0;
и 2≥0;
б) 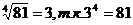 и 3≥0;
и 3≥0;
в) 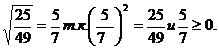
Из определения арифметического корня n-й степени следует, что при четом n подкоренное выражение должно быть больше или равно нулю, а значит и значение такого корня тоже неотрицательно, например:
арифметический корень 4-й степени из числа -81 не существует, так как ни одно число в четвертой степени не даст -81 ( при возведении в четную степень значение выражения всегда неотрицательно).
При нечетном показателе корня подкоренное выражение может быть отрицательным, и тогда минус может быть вынесен за знак коня.
Например: 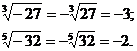
Уравнение хn=а.
Уравнение хn=а при нечетном n имеет единственное решение х= 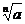 .
.
Например : х3=-125;
х= 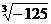 ;
;
х=- 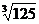 ;
;
х=-5.
Для наглядности сделаем проверку:
(-5)3=-125;
-125=-125- верно.
Ответ : х=-5.
Уравнение хn=а при четном n имеет и положительном а имеет два корня
х=± 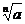 .
.
Например:
х4=16;
х1= 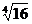 ; х2=-
; х2=- 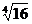 ;
;
х1=2; х2=-2.
Можно убедиться при проверке, что 24=16 и (-2)4=16.
Ответ : ±2.
Иногда нужно применить такое свойство арифметического корня n-й степени:
|х|, если n четно;
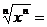 х, если n нечетно.
х, если n нечетно.
х, если х≥0;
 Вспомним, что |х|= -х, если х<0.
Вспомним, что |х|= -х, если х<0.
Например :
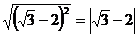 .
.
Так как 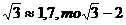 <0, следовательно
<0, следовательно
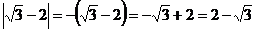 .
.

Для арифметического корня n-й степени, как и для квадратного корня, существуют операции внесения множителя под знак корня и вынесение множителя из-под знака корня.
Например :
2 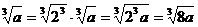 .
.
Из примера видно, что для внесения множителя под знак корня n-й степени его нужно
возвести в n-ю степень. Нужно помнить, что под знак с четным показателем мы имеем право внести только положительный множитель, например:
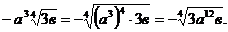
Аналогично производится вынесение множителя из-под знака корня , например:
а) 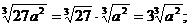
б) 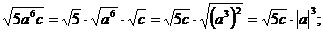
в) 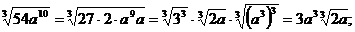
3.2
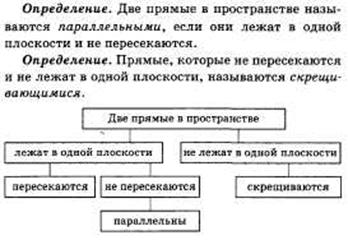
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
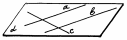 | a || b (прямая а параллельна прямой b) прямая с и прямая а не параллельны прямая с и прямая b не параллельны |
| рис. 8 |
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
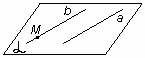 | M  a b||а и М a b||а и М  b (b - единственная) b (b - единственная) |
| рис. 9 |
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.
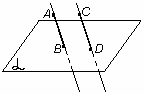 | отрезок СD || отрезку АВ | |||
| рис. 10 | ||||
Свойства параллельных прямых Свойство 1. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Свойство 2. Если две прямые параллельны третьей прямой, то они параллельны.
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. |

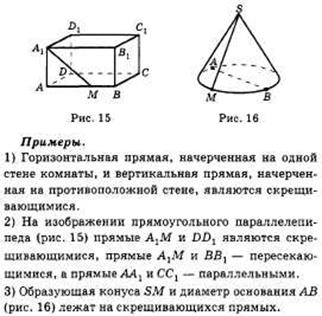
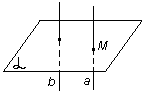 рис. 11
рис. 11 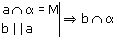
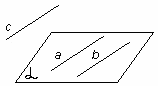 рис. 12
рис. 12