Определение матриц. Действие над ними.
Определение матриц. Действие над ними.
Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел aij, которые называют элементами матрицы и обозначается
 | (2.1) |
Заметим, что элементами матрицы могут быть не только числа. Представим себе, что вы описываете книги, которые стоят на вашей книжной полке. Пусть у вас на полке порядок и все книги стоят на строго определенных местах. Таблица, которая будет содержать описание вашей библиотеки (по полкам и следованию книг на полке), тоже будет матрицей. Но такая матрица будет не числовой. Другой пример. Вместо чисел стоят разные функции, объединенные между собой некоторой зависимостью. Полученная таблица также будет называться матрицей. Иными словами, Матрица, это любая прямоугольная таблица, составленная из однородных элементов. Здесь и далее мы будем говорить о матрицах, составленных из чисел.
Вместо круглых скобок для записи матриц применяют квадратные скобки или прямые двойные вертикальные линии
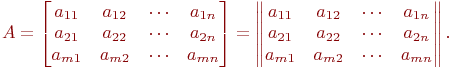 | (2.1*) |
Действия над матрицами и их свойства
1. Сложение матриц
Сложение: операция сложения матрицы вводится только для матриц одинаковых размеров.
Суммой двух матриц 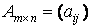 и
и 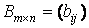 называется матрица
называется матрица 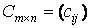 такая, что
такая, что 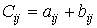
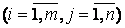 , например,
, например,
 ,
,  ,
,
тогда
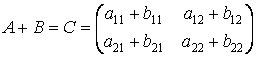 .
.
Аналогично определяется разность матриц.
2. Умножение матрицы на число
Произведением матрицы 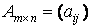 на число k называется матрица
на число k называется матрица 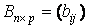 такая, что
такая, что 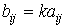
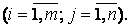
Примечание: матрица 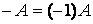 называется противоположной матрице
называется противоположной матрице 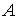 .
.
Операции сложения и умножения матрицы на число обладают следующими свойствами:
1) 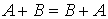 ;
;
2) 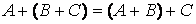 ;
;
3) 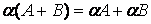 ;
;
4) 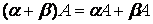 ;
;
5) 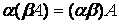 ;
;
6) 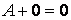 ;
;
7) 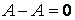 ;
;
8) 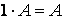 .
.
3. Умножение матрицы на матрицу
Мы будем всегда говорить, что умножение двух матриц возможно, если число столбцов первой матрицы равно числу строк второй матрицы:
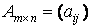 ;
; 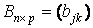 ;
; 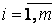 ;
; 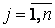 ;
; 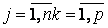 .
. 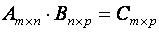 ,
,
где 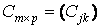 ;
; 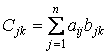 .
.
Например:
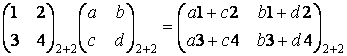 .
.
В общем случае 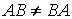 .
.
Продолжим перечисление свойств (см. п. 2.3.2):
9) 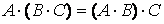 ;
;
10) 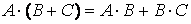 ;
;
11) 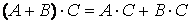 ;
;
12)  ;
;
13) 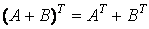 ;
;
14) 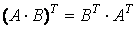 .
.
4. Элементарные преобразования матриц
К элементарным преобразованиям матриц относят:
– перестановку местами двух параллельных рядов матрицы;
– умножение всех элементов ряда матрицы на число, отличное от нуля;
– прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы 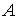 и
и 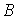 называются эквивалентными, т. е.
называются эквивалентными, т. е. 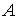 ~
~ 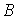 , если одна из них получается с помощью замен парных преобразований другой.
, если одна из них получается с помощью замен парных преобразований другой.
При получении элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
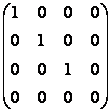 .
.
Вычисление определителей 2-го и 3-го порядков. Вычисления высших порядков.
Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: 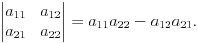
Действия над векторами.
Сложение векторов.
Опр. 6. Суммой двух векторов  и
и  является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
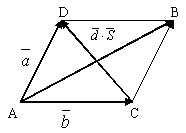
Рис.1.
Опр. 7.Суммойтрех векторов  ,
,  ,
, 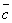 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8.Если А, В, С – произвольные точки, то 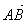 +
+ 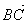 =
= 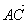 (правило треугольника).
(правило треугольника).
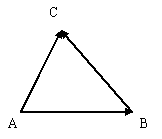
рис.2
Свойства сложения.
1о.  +
+  =
=  +
+  (переместительный закон).
(переместительный закон).
2о.  + (
+ (  +
+ 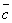 ) = (
) = (  +
+  ) +
) + 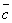 = (
= (  +
+ 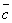 ) +
) +  (сочетательный закон).
(сочетательный закон).
3о.  + (–
+ (–  ) +
) + 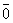 .
.
Вычитание векторов.
Опр. 9.Подразностью векторов  и
и  понимают вектор
понимают вектор 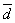 =
=  –
–  такой, что
такой, что  +
+ 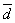 =
=  .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
Умножение вектора на число.
Опр. 10. Произведением вектора  на скаляр k называется вектор
на скаляр k называется вектор
 = k
= k  =
=  k,
k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора  , если k > 0;
, если k > 0;
2. противоположно направлению вектора  , если k < 0;
, если k < 0;
3. произвольно, если k = 0.
Действия над векторами.
Сложение векторов.
Опр. 6. Суммой двух векторов  и
и  является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).
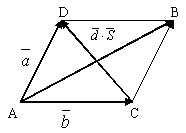
Рис.1.
Опр. 7.Суммойтрех векторов  ,
,  ,
, 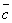 называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).
Опр. 8.Если А, В, С – произвольные точки, то 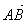 +
+ 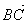 =
= 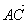 (правило треугольника).
(правило треугольника).
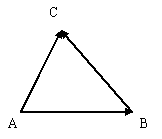
рис.2
Свойства сложения.
1о.  +
+  =
=  +
+  (переместительный закон).
(переместительный закон).
2о.  + (
+ (  +
+ 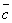 ) = (
) = (  +
+  ) +
) + 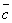 = (
= (  +
+ 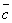 ) +
) +  (сочетательный закон).
(сочетательный закон).
3о.  + (–
+ (–  ) +
) + 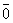 .
.
Вычитание векторов.
Опр. 9.Подразностью векторов  и
и  понимают вектор
понимают вектор 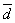 =
=  –
–  такой, что
такой, что  +
+ 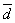 =
=  .
.
В параллелограмме – это другая диагональ СД (см.рис.1).
Умножение вектора на число.
Опр. 10. Произведением вектора  на скаляр k называется вектор
на скаляр k называется вектор
 = k
= k  =
=  k,
k,
имеющий длину ka, и направление, которого:
1. совпадает с направлением вектора  , если k > 0;
, если k > 0;
2. противоположно направлению вектора  , если k < 0;
, если k < 0;
3. произвольно, если k = 0.
Свойства векторов.
Опр. 11.Два вектора  и
и  называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.
Нулевой вектор 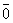 коллинеарен любому вектору.
коллинеарен любому вектору.
Теорема 1. Два ненулевых вектора  и
и  коллинеарны, Û когда они пропорциональны т.е.
коллинеарны, Û когда они пропорциональны т.е.
 = k
= k  , k – скаляр.
, k – скаляр.
Опр. 12. Три вектора  ,
,  ,
, 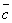 называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
называются компланарными, если они параллельны некоторой плоскости или лежат в ней.
Теорема 2. Три ненулевых вектора  ,
,  ,
, 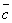 компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
компланарны, Û когда один из них является линейной комбинацией двух других, т.е.
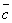 = k
= k  + l
+ l  , k ,l– скаляры.
, k ,l– скаляры.
Проекция вектора на ось.
Теорема 3.Проекция вектора  на ось (направленная прямая) l равна произведению длины вектора
на ось (направленная прямая) l равна произведению длины вектора  на косинус угла между направлением вектора и направлением оси, т.е.
на косинус угла между направлением вектора и направлением оси, т.е. 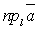 = a × cos a, a = Ð(
= a × cos a, a = Ð(  , l).
, l).
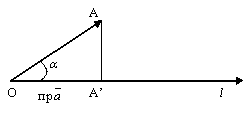
рис.3.
КООРДИНАТЫ ВЕКТОРА
Опр. 13. Проекции вектора  на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение:
на координатные оси Ох, Оу, Оz называются координатами вектора. Обозначение:  {ax, ay, az}.
{ax, ay, az}.
Длина вектора: 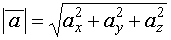

Пример:Вычислить длину вектора 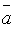
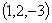 .
.
Решение: 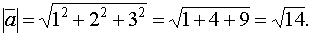
Расстояние между точками 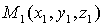 и
и 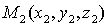 вычисляется по формуле:
вычисляется по формуле: 
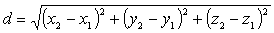 .
.
Пример:Найти расстояние между точками М (2,3,-1) и К (4,5,2).

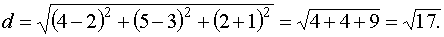
Базис системы векторов.
Определение.Под системой векторов понимают несколько векторов, принадлежащих одному и тому же пространству R.
Замечание. Если система состоит из конечного числа векторов, то их обозначают одной и той же буквой с разными индексами.
Пример. 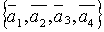
Определение.Любой вектор вида 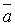 =
= 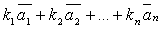 называется линейной комбинацией векторов
называется линейной комбинацией векторов 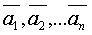 . Числа
. Числа 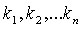 -коэффициентами линейной комбинации.
-коэффициентами линейной комбинации.
Пример. 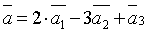 .
.
Определение. Если вектор 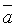 является линейной комбинацией векторов
является линейной комбинацией векторов 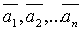 , то говорят, что вектор
, то говорят, что вектор 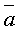 линейно выражается через векторы
линейно выражается через векторы 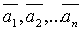 .
.
Определение. Система векторов называется линейно-независимой, если ни один вектор системы не может быть как линейная комбинация остальных векторов. В противном случае систему называют линейно-зависимой.
Пример. Система векторов 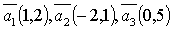 линейно-зависима, т. к. вектор
линейно-зависима, т. к. вектор 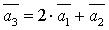 .
.
Определение базиса.Система векторов образует базис, если:
1) она линейно-независима,
2) любой вектор пространства через нее линейно выражается.
Пример 1.Базис пространства 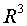 :
: 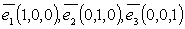 .
.
2. В системе векторов 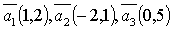 базисом являются векторы:
базисом являются векторы: 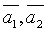 , т.к.
, т.к. 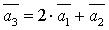 линейно выражается через векторы
линейно выражается через векторы 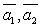 .
.
Замечание.Чтобы найти базис данной системы векторов необходимо:
1) записать координаты векторов в матрицу,
2) с помощью элементарных преобразований привести матрицу к треугольному виду,
3) ненулевые строки матрицы будут являться базисом системы,
4) количество векторов в базисе равно рангу матрицы.
Окружность и эллипс.
Окружность. Окружностью называется геометрическое место точек, равноудаленных от одной и той же точки.
Уравнение окружности имеет вид
(x - a)2 + (y - b)2 = r2,
где a и b - координаты центра окружности, а r - радиус окружности. Если же центр окружности находится в начале координат, то ее уравнение имеет вид
x2 + y2 = r2.
Эллипс. Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).
Простейшее уравнение эллипса
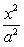
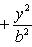
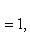
где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение
a2 - b2 = c2.
Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси
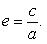
У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.
Пример задач:Написать уравнение окружности с центром в точке C(2, -3) и радиусом, равным 6.
Показать, что x2 + y2 + 4x - 6y - 3 = 0 есть уравнение окружности. Найти ее центр и радиус.
Найти координаты центра и радиус окружности x2 + y2 - x + 2y - 1 = 0.
Дана окружность x2 + y2 = 4. Составить уравнение прямой l, параллельной оси абсцисс и пересекающей окружность в таких точках M и N, чтоMN = 1.
Найти длину хорды, образующейся при пересечении прямой x + y - 5 = 0 и окружности (x + 1)2 + (y + 2)2 = 40.
Найти точки пересечения окружности (x - 1)2 + (y - 2)2 = 4 и прямой y = 2x.
Написать уравнение окружности, проходящей через три точки: (0, 1); (2, 0); (3, -1).
Найти уравнение окружности, касающейся оси Ox в начале координат и пересекающей ось Oy в точке A(0, 10).
Составить простейшее уравнение эллипса, зная, что: а) его полуоси a = 6, b = 4; б) расстояние между фокусами 2c = 10, а большая полуось 2a = 16; в) большая полуось a = 12, а эксцентриситет e = 0,5; г) малая полуось b = 8, а эксцентриситет e = 0,6; д) сумма полуосей a + b = 12, а расстояние между фокусами 2c=6*21/2.
Найти длины осей, координаты фокусов и эксцентриситет эллипса 4x2 + 9y2 = 144.
Составить уравнение окружности, проходящей через точку A (2; 1) и касающейся осей координат.
Отрезок BC длины l движется своими концами по сторонам прямого угла BOC. Какую линию опишет на этом отрезке точка A, разделяющая его в отношении λ(BA/AC = λ)?
Составить уравнение окружности, вписанной в треугольник, стороны которого лежат на прямых x = 0, y = 0 и 3x + 4y - 12 = 0.
Составить уравнение окружности, описанной около треугольника, образованного прямой 3x - y + 6 = 0 и осями координат.
Гипербола.
Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемыхфокусами есть величина постоянная, меньшая расстояния между фокусами.
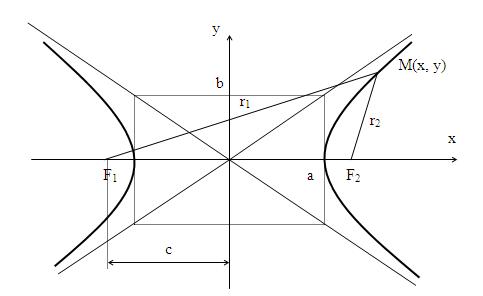
По определению | r 1 – r 2 | = 2 a . F 1 , F 2 – фокусы гиперболы. F 1 F 2 = 2 c .
Выберем на гиперболе произвольную точку М(х, у). Тогда :
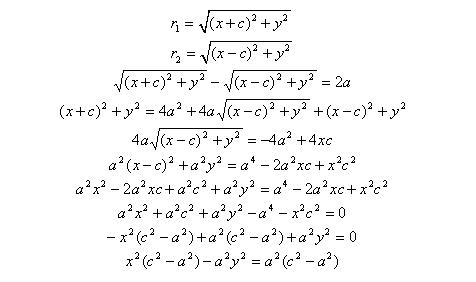
обозначим с2 – а2 = b2 (геометрически эта величина – меньшая полуось)
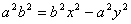
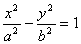
Получили каноническое уравнение гиперболы.Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.
Ось 2а называется действительной осью.
Ось 2 b называется мнимой осью.
Гипербола имеет две асимптоты, уравнения которых 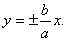
Определение. Отношение 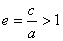 называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.
С учетом того, что с2 – а 2 = b2
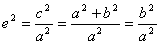 :
:
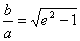
Если а = b , e = 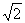 , то гипербола называется равнобочной (равносторонней).
, то гипербола называется равнобочной (равносторонней).
Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: 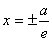
Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r / d – величина постоянная, равная эксцентриситету.
Доказательство. Изобразим схематично гиперболу.
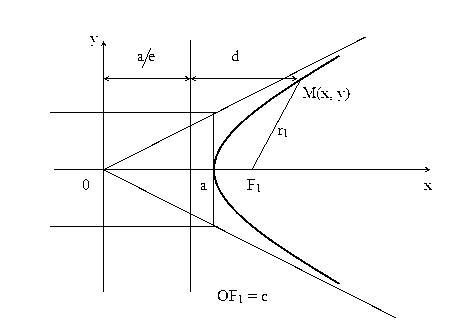
Из очевидных геометрических соотношений можно записать:
a / e + d = x , следовательно d = x – a / e .
( x – c ) 2 + y2 = r 2
Из канонического уравнения: 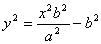 , с учетом b2 = c2 – a2:
, с учетом b2 = c2 – a2:
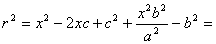
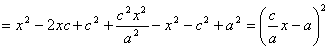
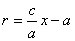
Тогда т.к. с/ a = e , то r = ex – a .
Итого: 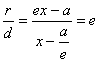
Для левой ветви доказательство аналогично. Теорема доказана
Пример 1 . Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 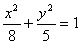
Для эллипса: c 2 = a2 – b2 .
Для гиперболы: c2 = a2 + b2 .
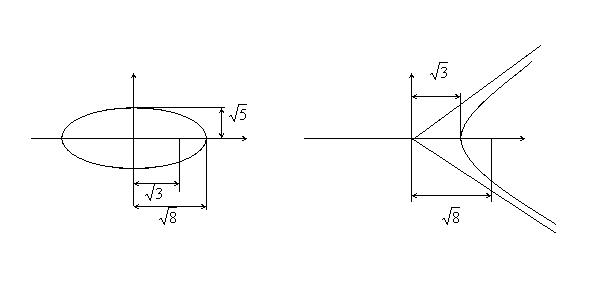
Уравнение гиперболы: 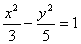
Пример 2 . Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением 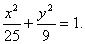
Находим фокусное расстояние c 2 = 25 – 9 = 16.
Длягиперболы: c2 = a2 + b2 = 16, e = c / a = 2; c = 2 a ; c 2 = 4 a2 ; a2 = 4;
b2 = 16 – 4 = 12.
Итого: 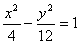 - искомое уравнение.
- искомое уравнение.
Парабола.
Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса 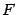 опустим перпендикуляр
опустим перпендикуляр 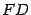 на директрису
на директрису 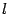 . Начало координат
. Начало координат 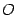 расположим на середине отрезка
расположим на середине отрезка 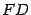 , ось
, ось 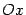 направим вдоль отрезка
направим вдоль отрезка 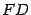 так, чтобы ее направление совпадало с направлением вектора
так, чтобы ее направление совпадало с направлением вектора 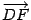 . Ось
. Ось 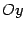 проведем перпендикулярно оси
проведем перпендикулярно оси 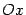 (рис. 12.15).
(рис. 12.15).
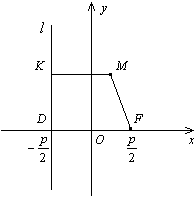
Рис.12.15.
Теорема 12.4 Пусть расстояние между фокусом 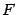 и директрисой
и директрисой 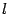 параболы равно
параболы равно 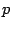 . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение
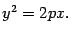 | (12.10) |
Доказательство. В выбранной системе координат фокусом параболы служит точка 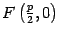 , а директриса имеет уравнение
, а директриса имеет уравнение 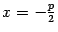 (рис. 12.15).
(рис. 12.15).
Пусть 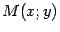 -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
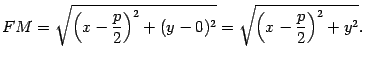
Расстоянием от точки 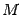 до директрисы
до директрисы 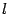 служит длина перпендикуляра
служит длина перпендикуляра 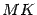 , опущенного на директрису из точки
, опущенного на директрису из точки 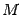 . Из рисунка 12.15 очевидно, что
. Из рисунка 12.15 очевидно, что 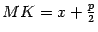 . Тогда по определению параболы
. Тогда по определению параболы 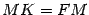 , то есть
, то есть
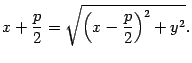
Возведем обе части последнего уравнения в квадрат:
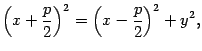
откуда
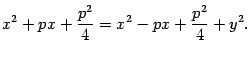
После приведения подобных членов получим уравнение (12.10).
Уравнение (12.10) называется каноническим уравнением параболы.
Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью 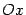 .
.
Доказательство. Проводится так же, как и доказательство (предложения 12.1).
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если переобозначить переменные 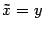 ,
, 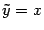 , то уравнение (12.10) можно записать в виде
, то уравнение (12.10) можно записать в виде
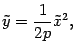
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).
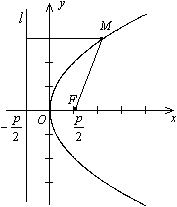
Рис.12.16.Парабола
Пример 12.6 Постройте параболу 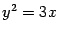 . Найдите ее фокус и директрису.
. Найдите ее фокус и директрису.
Решение. Уравнение является каноническим уравнением параболы, 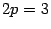 ,
, 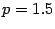 . Осью параболы служит ось
. Осью параболы служит ось 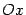 , вершина находится в начале координат, ветви параболы направлены вдоль оси
, вершина находится в начале координат, ветви параболы направлены вдоль оси 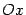 . Для построения найдем несколько точек параболы. Для этого придаем значения переменному
. Для построения найдем несколько точек параболы. Для этого придаем значения переменному 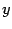 и находим значения
и находим значения 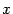 . Возьмем точки
. Возьмем точки 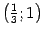 ,
, 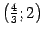 ,
, 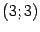 . Учитывая симметрию относительно оси
. Учитывая симметрию относительно оси 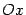 , рисуем кривую (рис. 12.17)
, рисуем кривую (рис. 12.17)
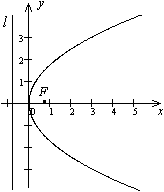
Рис.12.17.Парабола, заданная уравнением 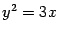
Фокус 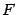 лежит на оси
лежит на оси 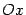 на расстоянии
на расстоянии 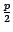 от вершины, то есть имеет координаты
от вершины, то есть имеет координаты 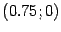 . Директриса
. Директриса 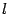 имеет уравнение
имеет уравнение 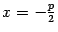 , то есть
, то есть 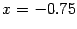 .
.
Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.
Предложение 12.5 Пусть 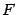 -- фокус параболы,
-- фокус параболы, 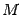 -- произвольная точка параболы,
-- произвольная точка параболы, 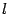 -- луч с началом в точке
-- луч с началом в точке 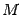 параллельный оси параболы. Тогда нормаль к параболе в точке
параллельный оси параболы. Тогда нормаль к параболе в точке 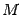 делит угол, образованный отрезком
делит угол, образованный отрезком 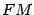 и лучом
и лучом 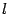 , пополам.
, пополам.
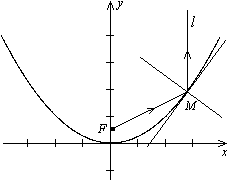
Рис.12.18.Отражение светового луча от параболы
Это свойство означает, что луч света, вышедший из фокуса 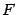 , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.
, отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.
Предел последовательности
Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого.
Частичный предел последовательности — это предел одной изеёподпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом.
Верхний предел последовательности — это наибольшая предельная точка этой последовательности.
Нижний предел последовательности — это наименьшая предельная точка этой последовательности.
Арифметические свойства
· Оператор взятия предела числовой последовательности является линейным, т. е. проявляет два свойства линейных отображений.
· Аддитивность. Предел суммы числовых последовательностей есть сумма их пределов, если каждый из них существует.
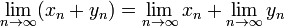
· Однородность. Константу можно выносить из-под знака предела.
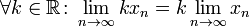
· Предел произведения числовых последовательностей факторизуется на произведение пределов, если каждый из них существует.
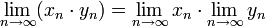
· Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.
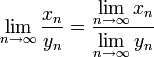
Эквивалентность определений
Все данные выше определения предела функции в точке эквивалентны.[1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.
Доказательство
· Сходящаяся функция локально сохраняет знак. Более обще,
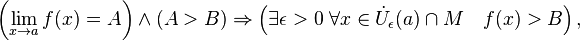
где 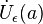 — проколотая окрестность точки
— проколотая окрестность точки 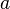 .
.
· В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
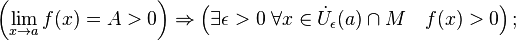
· Сходящаяся функция локально ограничена в окрестности предельной точки:
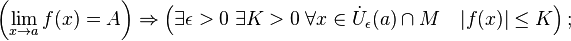
· Отделимость от нуля функций, имеющих предел, отличный от нуля.
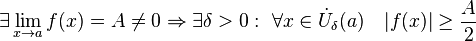
· Операция взятия предела сохраняет нестрогие неравенства.
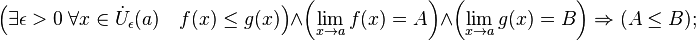
· Правило двух милиционеров
· Предел суммы равен сумме пределов:
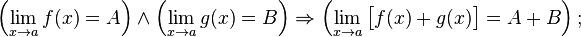
· Предел разности равен разности пределов:
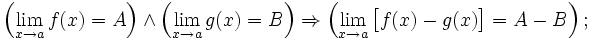
· Предел произведения равен произведению пределов:
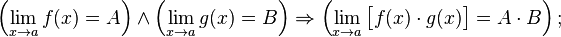
· Предел частного равен частному пределов.
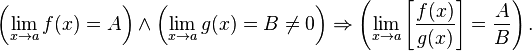
Определение
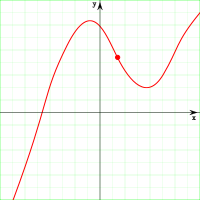
Пусть 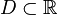 и
и 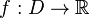 .
.
Функция 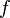 непрерывна в точке
непрерывна в точке 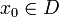 , если для любого
, если для любого 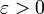 существует
существует 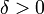 такое, что для любого
такое, что для любого
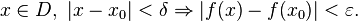
Функция 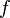 непрерывна на множестве
непрерывна на множестве 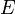 , если о
, если о
