Свойства транспонированных матриц.

Сложение матриц.

Суммой матриц 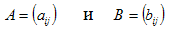одной и той же размерности называется матрица размерности 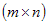, каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

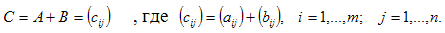
Матрицы разных размерностей складывать нельзя.

Пример1.
.

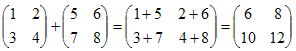Свойства сложения матриц.
1. Коммутативность.
A+B=B+A
2. Ассоциативность.
(A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α:

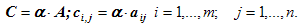
Пример 2.
.

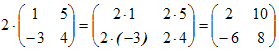Произведением матрицы 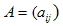размерности 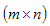на матрицу 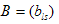размерности 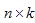называется матрица 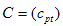размерности 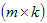, где:

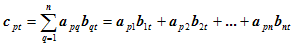
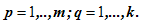
Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 3.

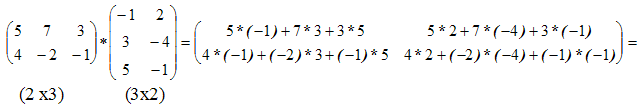
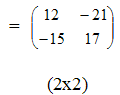
Пример 4.

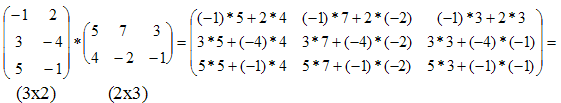
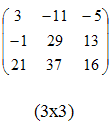
Результатом транспонирования матрицы 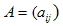размерности 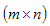является матрица 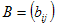размерности 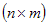, где

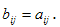
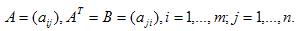
Пример 5.

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц:
(A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .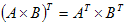

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице:
(A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической.

2)Определитель матрицы

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определение через разложение по первой строке

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

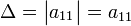
Для матрицы 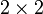детерминант определяется как

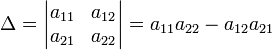
Для матрицы 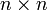определитель задаётся рекурсивно:

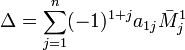, где 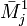— дополнительный минор к элементу a_1j. Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы 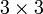такова:

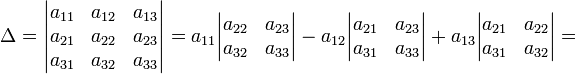
= a₁₁a₂₂a₃₃ − a₁₁a₂₃a₃₂ − a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ − a₁₃a₂₂a₃₁

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

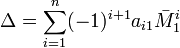
Также справедливо и аналогичное разложение по любой строке (столбцу):

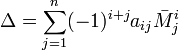
Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):

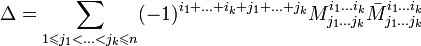
Свойства обратной матрицы

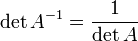• , где 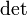обозначает определитель.
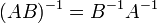• для любых двух обратимых матриц A и B.
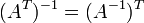• где * ^T обозначает транспонированную матрицу.
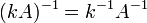• для любого коэффициента .
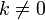• Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A ^{− 1} существует, то x = A ^{− 1}b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Точные (прямые) методы

Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ_i (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.

.

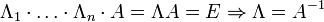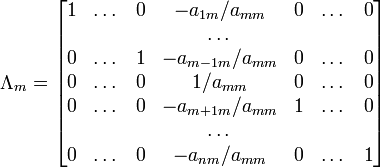Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O(n³).

Итерационные методы

Методы Шульца

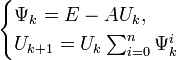
Оценка погрешности

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как:

или:

Ax = B.

Если к матрице А приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Методы решения

Прямые (или точные) методы позволяют найти решение за определённое количество шагов. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

6)Основные понятия систем линейных уравнений
Системы линейных уравнений: основные понятия

24 июня 2011

Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:

Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.

Определение. Решение системы уравнений — это последовательность чисел (k₁, k₂, ..., k_n), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x₁, x₂, ..., x_n дает верное числовое равенство.

Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:

1. Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
2. Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
3. Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.

Определение. Переменная x_i называется разрешенной, если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной x_i должен быть равен нулю.

Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:

Обе системы являются разрешенными относительно переменных x₁, x₃ и x₄. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x₁, x₃ и x₅. Достаточно переписать самое последнее уравнение в виде x₅ = x₄.

Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:

1. Число разрешенных переменных r равно общему числу переменных k: r = k. Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x₁ = b₁, x₂ = b₂, ..., x_k = b_k;
2. Число разрешенных переменных r меньше общего числа переменных k: r < k. Остальные (k − r) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.

Так, в приведенных выше системах переменные x₂, x₅, x₆ (для первой системы) и x₂, x₅ (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:

Теорема. Если в системе из n уравнений переменные x₁, x₂, ..., x_r — разрешенные, а x_{r + 1}, x_{r + 2}, ..., x_k — свободные, то:

1. Если задать значения свободным переменным (x_{r + 1} = t_{r + 1}, x_{r + 2} = t_{r + 2}, ..., x_k = t_k), а затем найти значения x₁, x₂, ..., x_r, получим одно из решений.
2. Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.

В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.

Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.

7)Метод Крамера. Решение систем линейных уравнений

Метод Крамера

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

Содержание [убрать] 1 Описание метода 2 Пример 3 Вычислительная сложность 4 Примечания

[править] Описание метода

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,...,b_n и x₁,x₂,...,x_n, либо набор c₁,c₂,...,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

8)Метод Гауса. Решение систем линейных уравнений

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные^[2].

Описание метода

Пусть исходная система выглядит следующим образом

Матрица A называется основной матрицей системы, b — столбцом свободных членов.

Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных ^[3].

Тогда переменные называются главными переменными. Все остальные называются свободными.

Если хотя бы одно число , где i > r, то рассматриваемая система несовместна.

Пусть для любых i > r.

Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 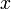( , где — номер строки):

,
где

Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

9)Понятие вектора. Операции над векторами

Определение: Направленный отрезок (или упорядоченная пара точек) называется вектором.

Вектор обычно обозначается символом , где А – начало, а В – конец направленного отрезка, либо одной буквой (в некоторых учебниках буква выделяется полужирным шрифтом; при этом стрелка опускается a). На чертеже вектор изображается стрелкой. Начало вектора называют точкой его приложения.

Расстояние между началом и концом вектора называется его длиной. Для обозначения длины вектора (его абсолютной величины) пользуются символом модуля. Так и обозначают длины соответствующих векторов.

Вектор единичной длины называют ортом.

К векторам будем относить и так называемый нулевой вектор, у которого начало и конец совпадают. Считается, что нулевой вектор не имеет определенного направления и имеет длину равную нулю. Это позволяет обозначать нулевой вектор вещественным числом 0 (нуль).

Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. Среди коллениарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы.

Векторы называются компланарными, если они лежат либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости.

Определение: Два вектора называются равными, если они: 1) коллинеарны; 2) равны по длине; 3) одинаково направлены.

Следствие: Для любого вектора и для любой точки А, существует, и притом единственная, точка B такая, что .

Мы не будем различать двух равных векторов, имеющих разные точки приложения. Такие векторы называются свободными (в отличие от скользящих и связанных векторов, встречающихся в других науках).

Понятие равенства векторов обладает следующими свойствами:

1. (рефлексивность).

2. Из того, что , следует (симметричность).

3. Из того, что и , следует (транзитивность).

Глава 2. Операции над векторами

Определение: Суммой двух векторов и называется вектор, имеющий начало в начале вектора , а конец – в конце вектора , при условии, что вектор приложен к концу вектора .

В соответствии с определением слагаемые и и их сумма образуют треугольник (рис.2). Поэтому данное правило сложения двух векторов называют «правилом треугольника».

Операция сложения векторов обладает свойствами:

1. (коммутативность);

2. , (ассоциативность);

3. для любого вектора (особая роль нулевого вектора);

4. для каждого вектора существует противоположный ему вектор такой, что (для получения достаточно поменять местами начало и конец вектора ).

Вектор противоположный вектору обозначают .

Определение: Разностью векторов и называется сумма вектора и вектора противоположного вектору , т.е. .
Разность получается из вектора сдвигом его начала в конец вектора , при условии, что векторы и имеют общее начало (рис.3). Очевидно, что для любого вектора .

Замечание: Существует еще одно правило сложения векторов, называемое «правилом параллелограмма»: векторы и прикладываются к общему началу О, и на них строится параллелограмм (рис. 4). Суммой будет вектор , расположенный на диагонали параллелограмма. Разностью здесь будет вектор , расположенный на второй диагонали.

Векторная алгебра имеет дело с двумя типами величин: векторами и числами. Числа обычно называют скалярными величинами или скалярами.

Определение: Произведением вектора на вещественное число λ (скаляр) называется вектор , такой, что 1) ; 2) вектор коллинеарен вектору ; 3) векторы и имеют одинаковое (противоположное) направление если λ > 0 (λ < 0).

Замечание: В случае, когда λ = 0 или произведение является нулевым вектором.

Операция умножения вектора на число обладает следующими свойствами:

1. (ассоциативное свойство сомножителей);

Действительно, заметим, что векторы, стоящие обеих частях равенства, имеют одну и ту же длину . Кроме того, они коллинеарны и одинаково направлены, так как их направление совпадает с направлением , если λ и μ одного знака, и противоположно направлению , если λ и μ имеют разные знаки. Если же λ или μ равны нулю, то обе части равенства равны нулю. Свойство доказано.

2. (свойства дистрибутивности).

Построим треугольник OAB где и . Построим далее треугольник SPQ, где и . Так как стороны SP, PQ треугольника SPQ параллельны и пропорциональны сторонам OA, AB треугольника OAB, то эти треугольники подобны. Поэтому сторона SQ также параллельна стороне OB и отношение их длин также равно |λ|. Ясно, далее, что и одинаково направлены, если λ > 0. Отсюда следует, что . Но и , а отсюда вытекает первое свойство дистрибутивности.

Очевидно, что векторы стоящие в обеих частях второго свойства дистрибутивности коллинеарны. Допустим сначала, что знаки λ и μ одинаковы. Тогда векторы и направлены одинаково и длина их суммы равна сумме их длин, т. е. . Но и следовательно, в этом случае векторы и равны по длине. Направление их совпадает с направлением вектора , если общий знак λ и μ положителен, и противоположно ему, если отрицателен. Допустим теперь, что знаки λ и μ различны, и для определенности будем считать |λ| > |μ|. В этом случае длина суммы равна разности длин, точнее . Но . Следовательно, и в этом случае длина вектора равна длине вектора . Очевидно, что оба эти вектора направлены так же, как . Если же |λ| = |μ| и знаки λ и μ противоположны, то обе части равенства равны нулю. То же обстоятельство имеет место, если равен нулю вектор или оба скаляра одновременно.

10)Вектора в прямоугольной декартовой системе координат

11)Уравнение прямой на плоскости

Линии второго порядка

Линии второго порядка, плоские линии, декартовы прямоугольные координаты которых удовлетворяют алгебраическому уравнению 2-й степени

a₁₁x² + a₁₂xy + a₂₂y² + 2a₁₃x + 2a₂₃y + a₁₁ = 0. (*)

Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Л. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий. Именно,

нераспадающиеся линии:

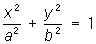— эллипсы,

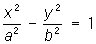— гиперболы,

y² = 2px — параболы,

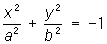— мнимые эллипсы;

распадающиеся линии:

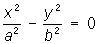— пары пересекающихся прямых,

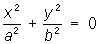— пары мнимых пересекающихся прямых,

x² - а² = 0 — пары параллельных прямых,

x² + а² = 0 — пары мнимых параллельных прямых,

x² = 0 — пары совпадающих параллельных прямых.

Исследование вида Л. в. п. может быть проведено без приведения общего уравнения к каноническому виду. Это достигается совместным рассмотрением значений т. н. основных инвариантов Л. в. п. — выражений, составленных из коэффициентов уравнения (*), значения которых не меняются при параллельном переносе и повороте системы координат:

, ,

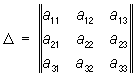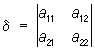S = a₁₁ + a₂₂, (a_ij = a_ji).

Так, например, эллипсы, как нераспадающиеся линии, характеризуются тем, что для них D ¹ 0; положительное значение инварианта d выделяет эллипсы среди других типов нераспадающихся линий (для гипербол d < 0, для парабол d = 0). Различить случаи действительного или мнимого эллипсов позволяет сопоставление знаков инвариантов D и S: если D и S разных знаков, эллипс действительный; эллипс мнимый, если D и S одного знака.

Три основные инварианта D, d и S определяют Л. в. п. (кроме случая параллельных прямых) с точностью до движения евклидовой плоскости: если соответствующие инварианты D, d и S двух линий равны, то такие линии могут быть совмещены движением. Иными словами, эти линии эквивалентны по отношению к группе движений плоскости (метрически эквивалентны).

Существуют классификации Л. в. п. с точки зрения др. групп преобразований. Так, относительно более общей, чем группа движений, — группы аффинных преобразований — эквивалентными являются любые две линии, определяемые уравнениями одного канонического вида. Например, две подобные Л. в. п. (см. Подобие)считаются эквивалентными. Связи между различными аффинными классами Л. в. п. позволяет установить классификация с точки зрения проективной геометрии, в которой бесконечно удалённые элементы не играют особой роли. Действительные нераспадающиеся Л. в. п.: эллипсы, гиперболы и параболы образуют один проективный класс — класс действительных овальных линий (овалов). Действительная овальная линия является эллипсом, гиперболой или параболой в зависимости от того, как она расположена относительно бесконечно удалённой прямой: эллипс пересекает несобственную прямую в двух мнимых точках, гипербола — в двух различных действительных точках, парабола касается несобственной прямой; существуют проективные преобразования, переводящие эти линии одна в другую. Имеется всего 5 проективных классов эквивалентности Л. в. п. Именно,

невырождающиеся линии

(x₁, x₂, x₃ — однородные координаты):

x₁² + x₂² — x₃² = 0 — действительный овал,

x₁² + x₂² + x₃² = 0 — мнимый овал,

вырождающиеся линии:

x₁² — x₂² = 0 — пара действительных прямых,

x₁² + x₂² = 0 — пара мнимых прямых,

x₁² = 0 — пара совпадающих действительных прямых.

13)Ф-ия. Способы задание ф-ии. Область определения и

область значения

Определение:

Николай Лобачевский 1834		Общее понятие требует, чтобы функцией от х называть число, которое дается для каждого х и вместе с каждым х постепенно изменяется
П.Лжен-Дирихле 1837		У есть функция переменной х (на отрезке а<=x<=b) , если каждому значению х (на этом отрезке) соответствует совершенно определенное значение у, причем безразлично, каким образом установлено это соответствие – аналитической формулой, графиком, таблицей либо даже просто словами

Область определения функции — множество, на котором задаётся функция.
Область значений функции — множество, которое получается в результате применения функции.

Способы задания функции:

• Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
• Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
• Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
• Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.

Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.(Пример:y=kx+b)

Нечётные и чётные функции — функции, графики которых обладают симметрией относительно изменения знака аргумента.

• Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).(Пример:y=1/x, y=x^3, y=sin x, y=tg x, y=ctg x, y=arcsin x, y=arctg x)
• Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).(Пример:y=|x|, y=x^2, y=cos x)

Периодическая функция ― функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).(Пример:Все тригонометрические функции)

Наименьшим положительным периодом функции называется такое число T, что T - период f, и ни одно положительное число, меньшее T, периодом f уже не является.

14)Основные характеристики ф-ий

Основные свойства функции.

1. Четность и нечетность

Функция называется четной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = f(x)

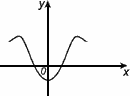
График четной функции симметричен относительно оси 0y

Функция называется нечетной, если
– область определения функции симметрична относительно нуля
– для любого х из области определения f(-x) = –f(x)

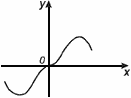
График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом 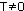, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

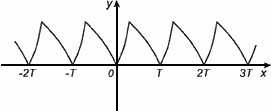
График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)< f(x₂).

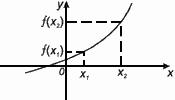
Функция f(x) убывает на множестве Р , если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁) > f(x₂).

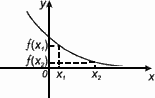
4. Экстремумы

Точка Х_max называется точкой максимума функции f(x) , если для <