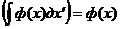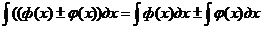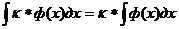Первообразная. Неопределенный интеграл и его св-ва.
Первообразная. Неопределенный интеграл и его св-ва.
интегрирование – операция, обратная дифференцированию.
Функция F(x) называется первообразной функции f(x), если производная F(x) равна f(x)
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x)
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
где С - произвольная постоянная.
Свойства неопределенного интеграла:
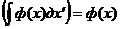
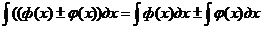
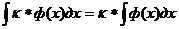
Методы интегрирования. Непосредственное интегрирование, метод подстановки
Для интегрирования многих функций применяют метод замены переменной, или подстановки, позволяющий приводить интегралы к табличной форме.
Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием. Наиболее общим приемом интегрирования функций является метод подстановки, который применяется тогда, когда искомый интеграл не являяется табличным, но путем ряда элементарных преобразований он может быть сведен к табличному.
Методы интегрирования. Интегрирование правильных и неправильных дробно рациональных функций
Дробно-рациональная функция называется правильной, если степень многочлена, стоящего в числителе, ниже степени многочлена в знаменателе, и неправильной в противном случае.
При интегрировании неправильной дроби следует предварительно перейти к правильной дроби путем выделения целой части.
Алгоритм:
Если дробь неправильная – выделить целую часть. Получим интеграл от целой части (интегрируется непосредственно) и интеграл от правильной дроби;
Если числитель равен дифференциалу знаменателя (или отличается от него постоянным множителем), то использовать замену переменной z=знаменатель;
Если числитель равен дифференциалу некого многочлена (или отличается от него постоянным множителем), а знаменатель равен степени того же многочлена, то использовать замену переменной z=знаменатель;
Теорема Лагранжа. Формула Ньютона-Лейбница и ее применение.
Если функция f(x) определена и непрерывна на отрезке ab ,то внутри отрезка ab обязательно отыщется по крайней мере 1 точка Xc,такая что выполняется равенство: f(b)-f(a)/b-a=f’(Xc)
Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции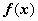 
, то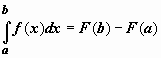 
(Формула Ньютона-Лейбница)
Формула Ньютона-Лейбница используется для нахождения площади фигуры,ограниченной 2 отрезками.
Дифферинциальные уравнения.Основные понятия и классификация.
1.Дифферинциальным называется уравнение ,содержащее производную искомой функции.
2.Уравнение,связывающее независимую переменную,искомую функцию и ее производные,называется дифферинциальным.
Решить ДУ,значит найти такую функцию,которая обратит это уравнение в верное равенство.
Порядком ДУ называется старший порядок производной искомой функции,входящей в него.
Классификация ДУ:1.с разделяющимися переменными,2.однородные,3.линейные,4.Бернулли,
Первообразная. Неопределенный интеграл и его св-ва.
интегрирование – операция, обратная дифференцированию.
Функция F(x) называется первообразной функции f(x), если производная F(x) равна f(x)
Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x)
Таким образом, если F - некоторая частная первообразная, то справедливо выражение
где С - произвольная постоянная.
Свойства неопределенного интеграла: