Mонотонные и ограниченные последовательности. Число е.

Последовательность 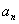называется

1. возрастающей, если ,
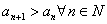2. убывающей, если .

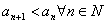Возрастающие и убывающие последовательности называются монотонными.
Последовательность 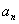называется ограниченной сверху, если все члены последовательности .
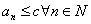Последовательность 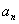называется ограниченной снизу, если все члены последовательности .
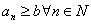Последовательность 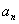называется ограниченной, если она ограничена и сверху, и снизу.
Пример: исследовать последовательность 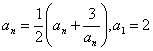на монотонность и ограниченность.
Решение:

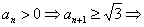1. ограничена снизу. (Если )
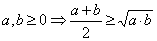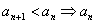2. убывает, поэтому 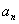ограничена сверху.

Ответ: последовательность ограничена и монотонно убывает.
Теорема Вейерштрасса: Монотонная и ограниченная последовательность имеет предел.
Число е.
Последовательность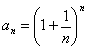

1. возрастает
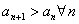
2. ограничена: 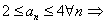по теореме Вейерштрасса 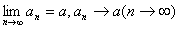.Его обозначают буквой e и называют числом e.

26 ВОПРОС

Непосредственное вычисление пределов, таблица пределов функций.

Непосредственное вычисление пределов основано на определении непрерывности функции в точке, на определении предела функции на бесконечности и на использовании свойств предела непрерывной функции.

Утверждение.

Значение предела в точке непрерывности функции равно значению функции в этой точке.

То есть, для основных элементарных функций (и функций полученных из основных элементарных с помощью элементарных преобразований графиков), опираясь на их известные свойства, предел в любой точке из области определения, кроме граничных, можно вычислять как значение соответствующей функции в этих точках.

Пример.

Вычислить предел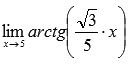

Решение.

Так как функция арктангенса непрерывна на всей области определения, то она непрерывна и в точке 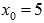. Следовательно, значение предела равно значению функции в этой точке.

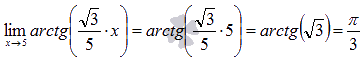
В граничных точках области определения вычисляются односторонние пределы. Например, для арксинуса и арккосинуса пр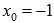и или .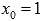

На плюс или минус бесконечности вычисляются соответствующие пределы пр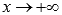и или 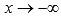на основании определеня предела функции на бесконечности.

Самые используемые свойства пределов.

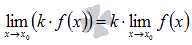1. , где k – коэффициент.

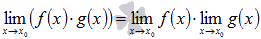1. , если в результате не выходит одна из неопределенностей пределов.

1. Для непрерывных функций знак предельного перехода и знак функции можно менять местами:
   

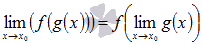
Массу пределов можно вычислить зная свйства основных элементарных функций. Приведем значение пределов этих функций в таблице, а ниже дадим разъяснения и несколько примеров с решениями. Все значения можно вычислить основываясь на определении предела функции в точке и на бесконечности.

Таблица пределов функций

Держите эту таблицу основных пределов перед глазами при решении задач и примеров. Она значительно упростит Вам жизнь.

27 вопрос

Предел функции

Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x₀, если для всех значений x, достаточно близких к x₀, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как

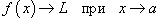
или через символ предела функции:

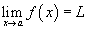
Если при прочтении данного материала у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме, также на форуме Вам помогут решить задачи по математике, геометрии, химии, теории вероятности и многим другим предметам.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

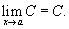
2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

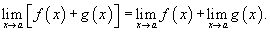
Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

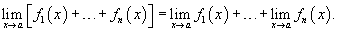
Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

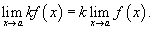
4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций: