Сходящиеся последовательности и их свойства.
Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число а, что последовательность {xn−a} является бесконечно малой.
Если последовательность {xn→a } является сходящейся и имеет своим пределом число a, то символически это записывают так:limn→∞xn=a или xn→a при n→∞
Определение. Последовательность {xn} называется сходящейся, если существует такое вещественное число a, что для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>Nэлементыxn этой последовательности удовлетворяют неравенству ∣xn−a∣<ε
При этом число a называется пределом последовательности.
Неравенство (5) можно записать в эквивалентной форме −ε<xn−a<+ε или, a−ε<xn<a+ε . (5')
Определение. Последовательность {xn} называется сходящейся, если существует такое число a, что в любой ε-окрестности точки aнаходятся все элементы последовательности {xn} начиная с некоторого номера (зависящего от ε).
Теорема 1. Сходящаяся последовательность имеет только один предел.
Доказательство. Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a . Последовательность {an−bn} является бесконечно малой, а в силу равенства an−bn=b−a все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числуb−a . Число b−a равно нулю, т. е. b=a. Теорема доказана.
Теорема 2. Всякая сходящаяся последовательность является ограниченной.
Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε при n≥N или, a−ε<xn<a+ε при n≥N . Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣∣x1∣∣,∣∣x2∣∣,...,∣∣хN−1∣∣ . Тогда, очевидно, ∣xn∣≤A для всех номеров n, а это и доказывает ограниченность последовательности {xn}. Теорема доказана.
Следствие 1. Не всякая ограниченная последовательность является сходящейся. Так, например, посл. 0,1,0,1,...,0,1, ... является
ограниченной, но не является сходящейся. В самом деле, обозначим n-й член этой последовательности символом xn и предположим, что эта последовательность сходится к некоторому пределу a. Но тогда каждая из последовательностей {xn+1−a} и {xn−a} являлась бы бесконечно малой. Стало быть, являлась бы бесконечно малой и разность этих последовательностей {xn+1−xn} а этого быть не может в силу того, что ∣∣xn+1−xn∣∣=1 для всех номеров n.
Последовательность {an} называется бесконечно малой, если для любого положительного вещественного числа ε найдется номер N(ε) такой, что при всех n>Nэлементan последовательности удовлетворяет неравенству ∣an∣<ε .
Теорема 3. Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}.
Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам а и b соответственно. Тогда в силу того что xn=a+an будут справедливы соотношения
xn=a+an,yn=b+bn, (6),
в которых anиbn представляют собой элементы некоторых бесконечно малых последовательностей {an} и {bn}. Из (6) вытекает, что(xn+yn)−(a−b)=an+bn . (7)
Т.к. сумма {an+bn} двух бесконечно малых последовательностей {an} и {bn} представляет собой бесконечно малую последовательность, то из соотношения (7) вытекает в силу определения, что последовательность {xn+yn} сходится и вещественное число a+b является ее пределом. Теорема доказана.
Теорема 4. Разность сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {xn} и {yn}
Доказательствоэтой теоремы аналогично доказательству Теоремы 3, только вместо соотношения (7) мы получим соотношение (xn−yn)−(a−b)=an−bn .
Теорема 5. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}.
Доказательство. Предположим, что последовательности {xn} и {yn}сходятся к пределам a и b соответственно. Тогда для элементов этих последовательностей справедливы (6), перемножая которые, мы получим
xn·yn=a·b+abn+ban+an·bn или, xnyn−a·b=abn+ban+an·bn (8)
Лемма 1. Если последовательность {yn} сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное {1yn} последовательностей {\{}1{\}} и {yn}, которое представляет собой ограниченную последовательность.
Теорема 6. Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}.
Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам a и b соответственно. В силу леммы 1 найдется номер N такой, что при n>N элементы ynнe обращаются в нуль, определена последовательность {1yn} и эта последовательность является ограниченной. Начиная с номера N, мы и будем
рассматривать частное {ynxn} . В силу определения достаточно доказать, что последовательность {ynxn−ba} является бесконечно малой. Будем исходить из тождества ynxn−ba=yn·bxn·b−yn·a (9)
Т.к. для элементов xn и yn справедливы (6), то
n·b−yn·a=(a+an)·bn−(b+bn)·an=anb−bna
Подставляя (10) в (9), получим ynxn−ba=1yn(an−babn) (11)
Остается доказать, что в правой части (11) стоит элемент бесконечно малой последовательности, но это сразу вытекает из того, что последовательность {1yn} (в силу леммы 1) является ограниченной, а последовательность {an−babn} (как разность двух бесконечно малых) является бесконечно малой последовательностью. Теорема доказана.
25 вопрос
Монотонная последовательность — это последовательность, элементы которой с увеличением номера не убывают, или, наоборот, не возрастают. Подобные последовательности часто встречаются при исследованиях и имеют ряд отличительных особенностей и дополнительных свойств. Последовательность из одного числа не может считаться возрастающей или убывающей.Определения
Пусть имеется множество  , на котором введено отношение порядка.
, на котором введено отношение порядка.
Последовательность 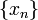 элементов множества
элементов множества  называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
называется неубывающей, если каждый элемент этой последовательности не превосходит следующего за ним.
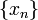 — неубывающая
— неубывающая 
Последовательность 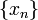 элементов множества
элементов множества  называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
называется невозрастающей, если каждый следующий элемент этой последовательности не превосходит предыдущего.
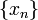 — невозрастающая
— невозрастающая 
Последовательность 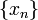 элементов множества
элементов множества  называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.
называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий.
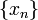 — возрастающая
— возрастающая 
Последовательность 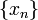 элементов множества
элементов множества  называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.
называется убывающей, если каждый элемент этой последовательности превышает следующий за ним.
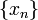 — убывающая
— убывающая 
Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.[1]
Последовательность называется строго монотонной, если она является возрастающей, либо убывающей.
Очевидно, что строго монотонная последовательность является монотонной.
Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно.
Промежутки монотонности
Может оказаться, что вышеуказанные условия выполняются не для всех номеров  , а лишь для номеров из некоторого диапазона
, а лишь для номеров из некоторого диапазона

(здесь допускается обращение правой границы  в бесконечность). В этом случае последовательность называется монотонной на промежутке
в бесконечность). В этом случае последовательность называется монотонной на промежутке  , а сам диапазон
, а сам диапазон  называется промежутком монотонности последовательности.
называется промежутком монотонности последовательности.
