ВОПРОС№1: Множество и действия с ними. Свойства введенных операций.
ВОПРОС№1: Множество и действия с ними. Свойства введенных операций.
Множество- совокупность элементов, объектов, отнесенных в единую группу по некоторым признакам.
Примеры множеств:
1. 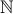 - множество натуральных чисел
- множество натуральных чисел
2. 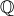 - множество рациональных чисел.
- множество рациональных чисел.
3. 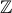 - множество целых чисел.
- множество целых чисел.
4. 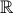 - множество действительных чисел.
- множество действительных чисел.
5. 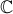 - множество комплексных чисел.
- множество комплексных чисел.
Действия над множествами
1)Объединение множеств:Результатом объединения множеств A и B будет являться множество C такое, что любой элемент множества C является элементом либо множества A, либо множества B.
Операция объединения множеств обозначается 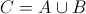
2) Пересечение множеств:Результатом пересечения множеств A и B будет являться множество C такое, что любой элемент множества C является одновременно и элементом множества A, и элементом множества B.
Операция пересечения множеств обозначается 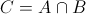
3) Разность множеств:Результатом разности множеств A и B будет являться множество C такое, что любой элемент множества C является элементом множества A, и не является элементом множества B.
Операция разность множеств обозначается: 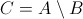
4) Дополнение множества:Дополнением множества A до множества B будет являться множество C такое, что любой элемент множества C яв-ся элементом множества B,и не является элементом множества A.
Операция дополнения множества обозначается 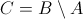
пример: дано:А={1;3;6;8}, B={2;4;6;8}Найти объединение,пересечение и разность множеств А и В. Решение: А 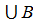 ={1;2;3;4;6;8}, A∩B = {6;8}, A\B={1,3}
={1;2;3;4;6;8}, A∩B = {6;8}, A\B={1,3}
Свойства введенных операций
1. A 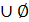 =A; A∩
=A; A∩ 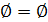 ; A\
; A\ 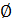 =
= 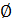 ;
; 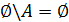 .
.
2. Коммутативность операций объединения и пересечения
A  B=B
B=B  A, A∩B=B∩A
A, A∩B=B∩A
3. Ассоциативность операций объединения и пересечения
(A  B)
B)  С=A
С=A 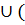 B
B  С); A
С); A 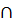 B)
B) 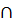 С=A
С=A 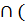 B
B 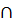 С)
С)
4. Идемпотентность операций объединения и пересечения
A  A=A; A
A=A; A 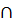 A=A
A=A
5. Дистрибутивность пересечения относительно объединения
A 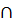 (B
(B  C)=(A
C)=(A 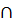 B)
B)  (A
(A 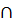 C)
C)
и дистрибутивность объединения относительно пересечения
A  (B
(B 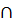 C)=(A
C)=(A  B)
B) 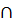 (A
(A  C)
C)
6. A\(A\B)=A 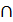 B
B
7. A\(B 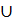 C)=(A\B)
C)=(A\B) 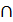 (A\C), A\(B
(A\C), A\(B 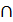 C)=(A\B)
C)=(A\B) 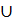 (A\C)
(A\C)
ВОПРОС№2: Отношение порядка на множестве действительных чисел и его свойства. Модуль действительного числа и его свойства.
Отношение порядка на множестве R. Для двух положительных действительных чисел
α= 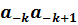 …
… 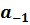 ,
, 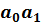 …
… 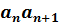 … ,
… ,
b= 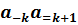 …
… 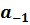 ,
, 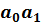 …
… 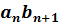 …, у которых до (n+1)-го разряда одинаковые цифры, полагаем α<b тогда и только тогда, когда
…, у которых до (n+1)-го разряда одинаковые цифры, полагаем α<b тогда и только тогда, когда 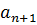 <
< 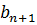 . Если b-положительное число, а число α-отрицательное или ноль, то всегда α<b. Если α и b – отрицательные числа, то α<b тогда и только тогда, когда
. Если b-положительное число, а число α-отрицательное или ноль, то всегда α<b. Если α и b – отрицательные числа, то α<b тогда и только тогда, когда 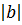 <
< 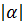 .
.
Свойства отношения порядка
1. Если α<b, b<c,то α<c
2. Если α<b,то существует действительное число с такое, что α<c<b
Модуль действительного числа и его свойства:
Модуль действительного числа α называетсясамо число α, если оно нуль или положительное. Если α является отрицательным числом, то его модулем будет положительное число. Модуль обозначается 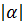
Свойства:
1) 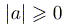 , причем
, причем 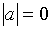 тогда и только тогда, когда
тогда и только тогда, когда 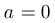 .
.
2) 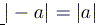 .
.
3) 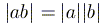 ; в частности,
; в частности, 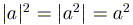 .
.
4) 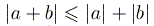 ;
; 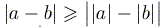 .
.
5) 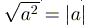 .
.
6) 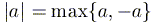 ; в частности
; в частности 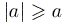 и
и 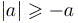 .
.
ВОПРОС№4: Уравнение прямой на плоскости. Геометрический смысл углового коэффицента.
Опред.1
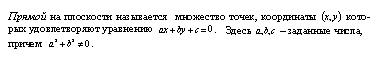
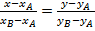 - уравнение прямой на плоскости.
- уравнение прямой на плоскости.
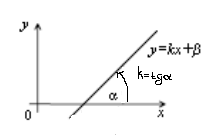 у= kх+β – уравнение прямой через угловой коэффициент.
у= kх+β – уравнение прямой через угловой коэффициент.
Геометрический смысл углового коэффициента
k= tgα –угловой коэффициент равен тангенсу угла между прямой и осью ОX.
ВОПРОС№10: Определения и основные действия с n-мерными векторами и их свойства.
Определение. Арифметическим n -мерным вектор-столбцом (или просто
n -мерным вектором) называется упорядочный набор из n действительных
чисел (1). Числа i x называются координатами вектора. Порядок чисел суще-
Ственен.
Определение. Произведением n -мерного вектора x на число a?R называ-
ется вектор вида:
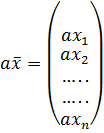
Определение. Суммой двух n -мерных векторов 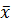 и
и 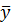 называются
называются
n -мерный вектор 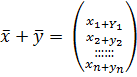
Нулевым вектором называется вектор, у которого все координаты равны
нулю. Он обозначается 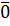 .
.
Свойства введённых операций:
1. 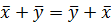 (коммуникативный закон сложения)
(коммуникативный закон сложения)
2. 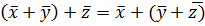 (ассоциативный закон сложения)
(ассоциативный закон сложения)
3. 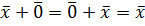
4. Для любого вектора 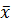 существует вектор (-
существует вектор (- 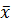 )=
)= 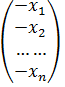 такой, что
такой, что 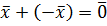
5. 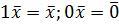
6. Для любых чисел a,b и для любого вектора 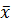 выполнены равенства:
выполнены равенства:
6.1. a( b 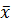 ) = ( ab )
) = ( ab ) 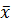 .
.
6.2. ( a + b ) 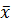 = a
= a 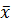 + b
+ b 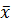
7. Для любого числа a и для любых векторов 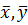 выполнено равенство
выполнено равенство
a( 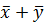 ) a
) a 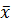 a
a 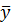 .
. 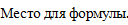
Множество арифметических n -мерных векторов с введенными операциями
сложения и умножения векторов на действительные числа называется
n -мерным линейным вещественным пространством. Оно обозначается
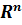 .
.
Пространство 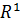 – это числовая ось,
– это числовая ось, 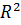 – числовая плоскость и так далее.
– числовая плоскость и так далее.
Норма вектора и ее свойство
Определение. Нормой вектора 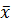 из
из 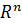 называется число
называется число
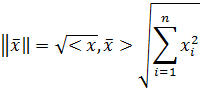
Свойства нормы
1. 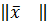 ≥0 и
≥0 и 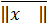 =0 ⇔
=0 ⇔ 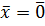
2. Для любого числа a и для любого вектора 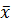 выполняется
выполняется 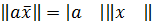 , в самом деле
, в самом деле
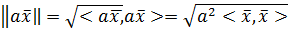
3.Для любых векторов 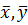 выполнено неравенство
выполнено неравенство 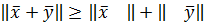
ВОПРОС№12: Определения, основные действия с матрицами и их свойства
Основные понятия
Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или у столбцов одинаковой длины). Матрица записывается в виде

или, сокращенно,A=(aij) (i=1,m, j=1,n) i-номер строки,(т.е.i=1,2,3..m),j-номер столбца.
Матрицу А называют матрицей размера m x n и пишут Аmxn.Числа aij составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.
А=В,если aij=bij (i=1,m, j=1,n)
Пример:
 Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.
В матричном исчислении матрицы О и E играют роль чисел 0 и 1 в арифметике.
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:
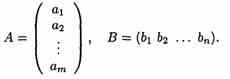
Матрица размера 1х1, состоящая из одного числа, отождествляется с этим числом,
т.е. (5)1х1 есть 5.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается АТ
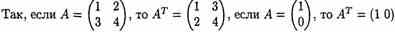
Транспонированная матрица обладает следующим свойством: (АТ)Т=А
Действия над матрицами
Сложение
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц Amxn=(aij) Bmxn=(bij) называется матрица Cmxn=(cij) такая, что cij=aij+bij (i=1,m, j=1,n)
<< Пример 1.2
Аналогично определяется разность матриц.
Умножение на число
Произведением матрицы. Amxn=(aij) на число k называется матрица Bmxn=(bij),такая, что.bij=k*aij (i=1,m, j=1,n)
<< Пример 1.3
Матрица -А = (-l)*A называется противоположной матрице А.
Разность матриц А-В можно определить так: А-В=А+(-В). Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А+В=В+А
2. А+(В+С)=(А + В) + С
3. А+О=А
4. А-А=О
5. 1*А=А;
6. а*(А+В)=аА+аВ;
7. (а+в)*А=аА+вА
8. а*(вА)=(ав)*А,
где А, В, С — матрицы, а и в-числа.
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
· перестановка местами двух параллельных рядов матрицы;
· умножение всех элементов ряда матрицы на число, отличное от нуля;
· прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю.
Такую матрицу называют канонической, например
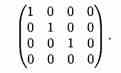
Произведение матриц
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведение матрицы на матрицу называется матрица такая, что
cik=ai1*b1k+ai2*b2k+…+ain*bnk. где (i=1,m, j=1,n)
т. е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-гo столбца матрицы В.
Получение элемента Cik схематично изображается так:
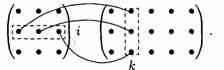
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А*Е=Е*А=А, где А-квадратная матрица, Е-единичная матрица того же размера.
Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами:
1. А*(В*С)=(А*В)*С;
2. А * (В + С) = АВ + АС
3. (А+В)*С=АС+ВС;
4. а(АВ) = (аА)В,
если, конечно, написанные суммы и произведения матриц имеют смысл. Для операции транспонирования верны свойства:
(A+B)T=AT+BT
(АВ)Т=ВTАT
Свойства определителей.
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1. («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.
Иными словами:
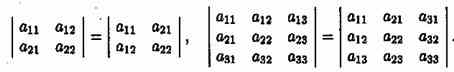
В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно,
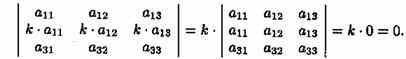
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента aij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается mij
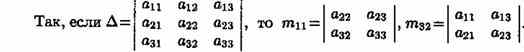
Алгебраическим дополнениемэлемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j — четное число, и сознаком «минус», если эта сумма нечетная. Обозначается
Aij: Aij=(-1)i+j*mij.
Так A11=+m11,A32=-m32.
Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что
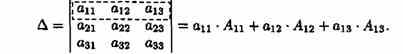
В самом деле, имеем
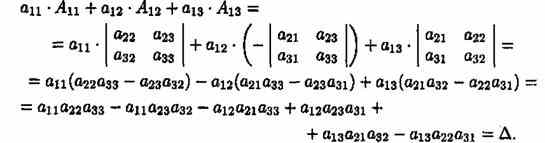
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например, a11A21+a12A22+a13A23=0.
ВОПРОС№13: Квадратные матрицы, их определители и способы их вычисления.Если число столбцов матрицы равно числу ее строк (I = J = N), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.
Единичной матрицей (обозначается I, а иногда E) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.
важной характеристикой квадратной матрицы является ее определитель (обозначается det(A)). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда
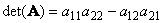
Для матрицы (3×3) определитель будет равен
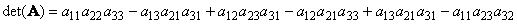
Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент а11:
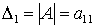 .
.
ВОПРОС№14:Метод Гауса и Крамера решения СЛАУ.
Опред.1 Cистема вида 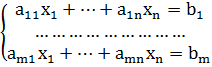 , где aij – некоторые действительные числа называется система линейных алгебраических уравнений (СЛАУ).
, где aij – некоторые действительные числа называется система линейных алгебраических уравнений (СЛАУ).
Опред.2 Элементарные преобразовании системы это такие преобразования системы, когда исходная и преобразованная системы имеют одно и тоже решение.
1⁰ Умножение строки на любое число отличное от 0.
2⁰ Перестановка местами 2-х строк.
3⁰ Прибавление (вычитание) к строке любой другой строки, умноженной на некоторое число.
4⁰ вычеркивание нулевой строки.
Метод Гауса решения СЛАУ.
1⁰приведение исходной системы к системе ступенчатого вида с помощью элементарных преобразований.
2⁰ Решение системы ступенчатого вида.
3⁰ Запись общего решения.
Метод Крамера решения СЛАУ
1⁰ Находим определитель матрицы ∆=|A|
2⁰∆=0 (система не имеет решений)
3⁰ Находим ∆х; х= 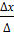
4⁰ Находим ∆у; у= 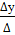
5⁰ Находим ∆z; z 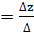
6⁰ Записываем ответ.
Производная произведения
Производная произведения считается совсем по другой формуле. А именно:
(f · g) ’ = f ’ · g + f · g ’
Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.
· Задача. Найти производные функций: f(x) = x3 · cos x; g(x) = (x2 + 7x − 7) · ex.
Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x3 · cos x)’ = (x3)’ · cos x + x3 · (cos x)’ = 3x2 · cos x + x3 · (− sin x) = x2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x2 + 7x − 7) · ex)’ = (x2 + 7x − 7)’ · ex + (x2 + 7x − 7) · (ex)’ = (2x + 7) · ex + (x2 + 7x − 7) · ex = ex · (2x + 7 + x2 + 7x −7) = (x2 + 9x) · ex = x(x + 9) · ex.
Ответ:
f ’(x) = x2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · ex.
Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.
Производная частного
Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:
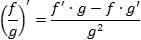
Неслабо, да? Откуда взялся минус? Почему g2? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.
Задача. Найти производные функций: f(x) = x3 · cos x; g(x) = (x2 + 7x − 7) · ex.
Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:
f ’(x) = (x3 · cos x)’ = (x3)’ · cos x + x3 · (cos x)’ = 3x2 · cos x + x3 · (− sin x) = x2 · (3cos x − x · sin x)
У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:
g ’(x) = ((x2 + 7x − 7) · ex)’ = (x2 + 7x − 7)’ · ex + (x2 + 7x − 7) · (ex)’ = (2x + 7) · ex + (x2 + 7x − 7) · ex = ex · (2x + 7 + x2 + 7x −7) = (x2 + 9x) · ex = x(x + 9) · ex.
Ответ:
f ’(x) = x2 · (3cos x − x · sin x);
g ’(x) = x(x + 9) · ex
Интегрирование по частям.
Интегрирование по частям основано на представлении подынтегрального выражения в виде произведения 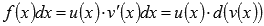 и последующем применении формулы
и последующем применении формулы 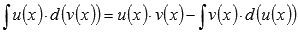 . Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
. Этот метод является очень мощным инструментом интегрирования. В зависимости от подынтегральной функции, метод интегрирования по частям иногда приходится применять несколько раз подряд до получения результата. Для примера найдем множество первообразных функции арктангенс.
Пример.Вычислить неопределенный интеграл 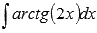 .
.
Решение.Пусть 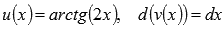 , тогда
, тогда
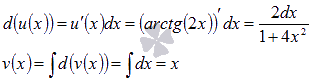
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.
Теперь применяем формулу интегрирования по частям:
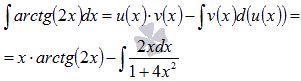
Последний интеграл вычислим по методу подведения под знак дифференциала.
Так как 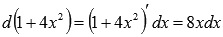 , то
, то 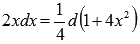 . Поэтому
. Поэтому 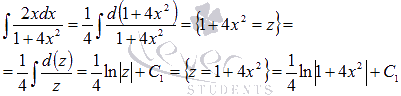
Следовательно,
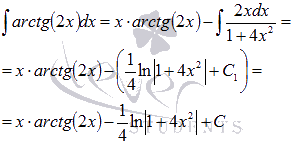
где 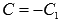 . Ответ:
. Ответ: 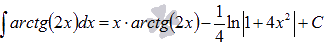 .
.
ВОПРОС№1: Множество и действия с ними. Свойства введенных операций.
Множество- совокупность элементов, объектов, отнесенных в единую группу по некоторым признакам.
Примеры множеств:
1. 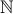 - множество натуральных чисел
- множество натуральных чисел
2. 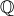 - множество рациональных чисел.
- множество рациональных чисел.
3. 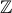 - множество целых чисел.
- множество целых чисел.
4. 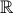 - множество действительных чисел.
- множество действительных чисел.
5. 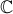 - множество комплексных чисел.
- множество комплексных чисел.
Действия над множествами
1)Объединение множеств:Результатом объединения множеств A и B будет являться множество C такое, что любой элемент множества C является элементом либо множества A, либо множества B.
Операция объединения множеств обозначается 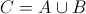
2) Пересечение множеств:Результатом пересечения множеств A и B будет являться множество C такое, что любой элемент множества C является одновременно и элементом множества A, и элементом множества B.
Операция пересечения множеств обозначается 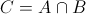
3) Разность множеств:Результатом разности множеств A и B будет являться множество C такое, что любой элемент множества C является элементом множества A, и не является элементом множества B.
Операция разность множеств обозначается: 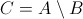
4) Дополнение множества:Дополнением множества A до множества B будет являться множество C такое, что любой элемент множества C яв-ся элементом множества B,и не является элементом множества A.
Операция дополнения множества обозначается 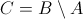
пример: дано:А={1;3;6;8}, B={2;4;6;8}Найти объединение,пересечение и разность множеств А и В. Решение: А 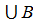 ={1;2;3;4;6;8}, A∩B = {6;8}, A\B={1,3}
={1;2;3;4;6;8}, A∩B = {6;8}, A\B={1,3}
Свойства введенных операций
1. A 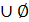 =A; A∩
=A; A∩ 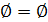 ; A\
; A\ 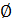 =
= 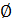 ;
; 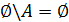 .
.
2. Коммутативность операций объединения и пересечения
A  B=B
B=B  A, A∩B=B∩A
A, A∩B=B∩A
3. Ассоциативность операций объединения и пересечения
(A  B)
B)  С=A
С=A 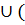 B
B  С); A
С); A 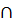 B)
B) 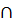 С=A
С=A 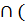 B
B 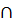 С)
С)
4. Идемпотентность операций объединения и пересечения
A  A=A; A
A=A; A 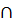 A=A
A=A
5. Дистрибутивность пересечения относительно объединения
A 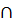 (B
(B  C)=(A
C)=(A 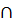 B)
B)  (A
(A 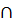 C)
C)
и дистрибутивность объединения относительно пересечения
A  (B
(B 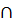 C)=(A
C)=(A  B)
B) 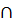 (A
(A  C)
C)
6. A\(A\B)=A 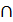 B
B
7. A\(B 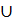 C)=(A\B)
C)=(A\B) 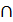 (A\C), A\(B
(A\C), A\(B 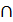 C)=(A\B)
C)=(A\B)  (A\C)
(A\C)
