Бесконечно большие и бесконечно малые последовательности
Определение. Последовательность { хn} называется бесконечно большой, если для как угодно большого любого положительного числа А существует номер N, зависящий от этого числа А, такой, что для всех последующих номеров n > N выполняется неравенство | xn | > A:
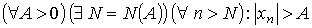
Замечание. Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n + 1, … не является бесконечно большой, поскольку при A > 1 неравенство | xn| > A выполняется не для всех элементов xn с нечетными номерами.
Определение. Последовательность {αn} называется бесконечно малой, если для любого как угодно малого положительного числа ε > 0 существует номер N, зависящий от этого ε, такой, что для любых n > N выполняется неравенство |αn| < ε:
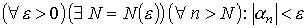
Свойства бесконечно малых и бесконечно больших величин
и связь между ними
Пусть f1 (x) и f 2 (x) бесконечно малые величины при 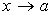 ,
,
т.е. 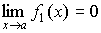 и
и 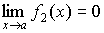 .
.
1. Сумма (разность) бесконечно малых величин есть величина бесконечно малая:
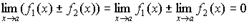 . (4.17)
. (4.17)
2. Произведение бесконечно малых величин есть величина бесконечно малая:
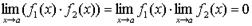 . (4.18)
. (4.18)
3. Произведение бесконечно малой величины на константу С или на функцию, имеющую конечный предел 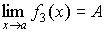 , есть величина бесконечно малая:
, есть величина бесконечно малая:
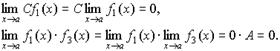 .
.
Пусть 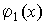 и
и 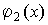 бесконечно большие величины при
бесконечно большие величины при 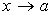 ,
,
т.е. 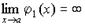 и
и 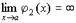 .
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
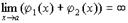 .
.
2. Произведение бесконечно больших величин есть величина бесконечно большая:
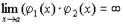 .
.
3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел 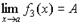 , есть величина бесконечно большая:
, есть величина бесконечно большая:
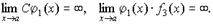
26) Теорема о двух милиционерах — теорема в математическом анализе о существовании предела у функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел. Формулируется следующим образом:
Если функция y = f(x) такая, что 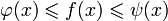 для всех x в некоторой окрестности точки a, причем функции φ(x) и ψ(x) имеют одинаковый предел при для всех x в некоторой окрестности точки a, причем функции φ(x) и ψ(x) имеют одинаковый предел при 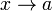 , то существует предел функции y = f(x) при , то существует предел функции y = f(x) при 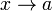 , равный этому же значению, то есть , равный этому же значению, то есть 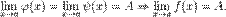 Равномерная сходимость. Отличие равномерной сходимости от поточечной в том, что скорость сходимости не зависит от точки. Определение. Последовательность функций fn : X ! R равномерно сходится на X к функции f, если 8" > 0 9N = N(") 8x 2 X (n > N ) jfn(x) f(x)j < "): Равномерная сходимость обозначается через fn(x) f(x). Природа множества X здесь никакой роли не играет. Можно считать, что X Rk. Дальше потребуется, чтобы X было компактно и измеримо (по Жордану). При необходимости уменьшить затрудняющий продвижение дискомфорт, первоначально полезно думать, что X является просто отрезком числовой оси. Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии не более чем заданное. Определение Последовательность точек Равномерная сходимость. Отличие равномерной сходимости от поточечной в том, что скорость сходимости не зависит от точки. Определение. Последовательность функций fn : X ! R равномерно сходится на X к функции f, если 8" > 0 9N = N(") 8x 2 X (n > N ) jfn(x) f(x)j < "): Равномерная сходимость обозначается через fn(x) f(x). Природа множества X здесь никакой роли не играет. Можно считать, что X Rk. Дальше потребуется, чтобы X было компактно и измеримо (по Жордану). При необходимости уменьшить затрудняющий продвижение дискомфорт, первоначально полезно думать, что X является просто отрезком числовой оси. Фундаментальная последовательность, или сходящаяся в себе последовательность, или последовательность Коши — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии не более чем заданное. Определение Последовательность точек 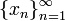 метрического пространства (X,ρ) называется фундаментальной, если она удовлетворяет критерию Коши: метрического пространства (X,ρ) называется фундаментальной, если она удовлетворяет критерию Коши:
|
27) Функция f (отображение, операция, оператор) — это закон или правило, согласно которому каждому[3] элементу x из множества X ставится в соответствие единственный элемент y из множества Y.[4]
При этом говорят, что функция f задана на множестве X, или что f отображает X в Y.
Если элементу 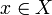 сопоставлен элемент
сопоставлен элемент 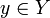 , то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называется областью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений или областью изменения
, то говорят, что элемент y находится в функциональной зависимости f от элемента x. При этом переменная x называется аргументом функции f или независимой переменной, множество X называется областью задания или областью определения функции, а элемент y, соответствующий конкретному элементу x — частным значением функции f в точке x. Множество Y всех возможных частных значений функции f называется её областью значений или областью изменения
Число A называется пределом функции 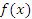 при
при 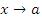 , если для любого произвольно малого числа ε > 0 существует такое число δ(ε), что для всех x, удовлетворяющих условию
, если для любого произвольно малого числа ε > 0 существует такое число δ(ε), что для всех x, удовлетворяющих условию
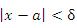 | (11) |
выполняется неравенство
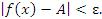 | (12) |
Для обозначения предела функции 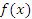 при
при 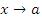 используется символическое выражение
используется символическое выражение
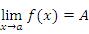
или запись вида
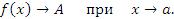
.Равномерная сходимость последовательности функций (отображений) — свойство последовательности 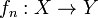 , где X — произвольное множество, Y = (Y,d) — метрическое пространство,
, где X — произвольное множество, Y = (Y,d) — метрическое пространство, 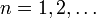 сходится к функции (отображению)
сходится к функции (отображению) 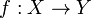 , означающее, что для любого
, означающее, что для любого 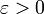 существует такой номер Nε, что для всех номеров n > Nε и всех точек
существует такой номер Nε, что для всех номеров n > Nε и всех точек 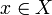 выполняется неравенство
выполняется неравенство
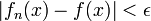
Обычно обозначается 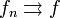 .
.
Это условие равносильно тому, что
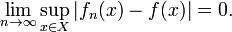
28)Первый замечательный предел:
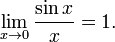
29) Второй замечательный предел:
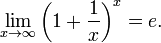
32) Определение
Пусть в некоторой окрестности точки 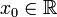 определена функция
определена функция 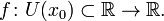 Производной функции называется такое число
Производной функции называется такое число 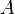 , что функцию в окрестности U(x0) можно представить в виде
, что функцию в окрестности U(x0) можно представить в виде
f(x0 + h) = f(x0) + Ah + o(h)
если 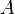 существует.
существует.

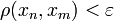 для всех n,m > Nε.
для всех n,m > Nε.