Разложение вектора по базису векторного пространства.

Пусть произвольные векторы 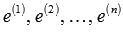являются базисом n-мерного векторного пространства. Если к ним добавить некоторый n-мерный вектор x, то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам.

Так мы подошли к очень важной теореме.

Теорема.

Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.

Доказательство.

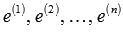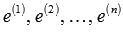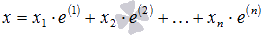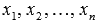Пусть - базис n-мерного векторного пространства. Добавим к этим векторам n-мерный вектор x. Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где - некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.

Предположим, что существует еще одно разложени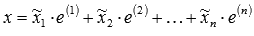е , где 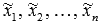- некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :

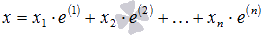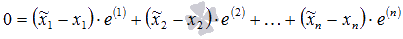
Так как система базисных векторов 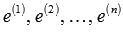линейно независима, то поопределению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты 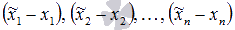равны нулю. Поэтому, 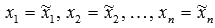, что доказывает единственность разложения вектора по базису.

Определение.

Коэффициенты 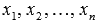называются координатами вектора x в базисе .

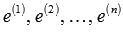После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n-мерный вектор 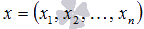». Это выражение означает, что мы рассматриваем вектор x n-мерного векторного пространства, координаты 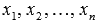которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор x в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от .

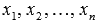Рассмотрим следующую задачу.

Пусть в некотором базисе n-мерного векторного пространства нам задана система из nлинейно независимых векторов

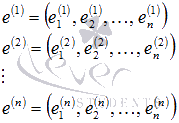
и вектор 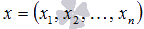. Тогда векторы 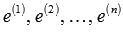также являются базисом этого векторного пространства.

Пусть нам требуется найти координаты вектора x в базисе 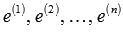. Обозначим эти координаты как .

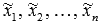Вектор x в базисе 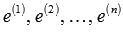имеет представление 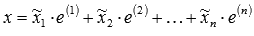. Запишем это равенство в координатной форме:

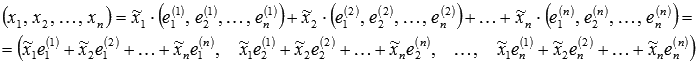
Это равенство равносильно системе из n линейных алгебраических уравнений с nнеизвестными переменными :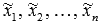

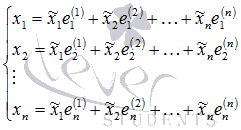
Основная матрица этой системы имеет вид

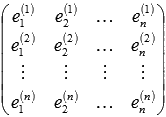
Обозначим ее буквой А. Строки матрицы А представляют собой векторы линейно независимой системы векторов 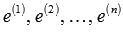, поэтому ранг этой матрицы равен n, следовательно, ее определитель отличен от нуля. Этот факт указывает на то, что система уравнений имеет единственное решение, которое может быть найдено любым методом, например, методом Крамера или матричным методом.

Так будут найдены искомые координаты 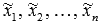вектора x в базисе .

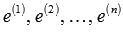Разберем теорию на примерах.

Пример.

В некотором базисе трехмерного векторного пространства заданы векторы

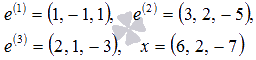
Убедитесь, что система векторов 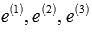также является базисом этого пространства и найдите координаты вектора x в этом базисе.

Решение.

Чтобы система векторов 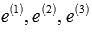была базисом трехмерного векторного пространства нужно, чтобы она была линейно независима. Выясним это, определив ранг матрицы A, строками которой являются векторы 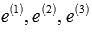. Ранг найдем методом Гаусса

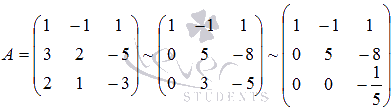
следовательно, Rank(A) = 3, что показывает линейную независимость системы векторов .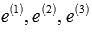

Итак, векторы 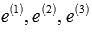являются базисом. Пусть в этом базисе вектор x имеет координаты 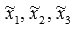. Тогда, как мы показали выше, связь координат этого вектора задается системой уравнений

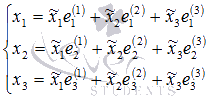
Подставив в нее известные из условия значения, получим

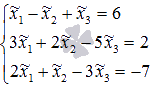
Решим ее методом Крамера:

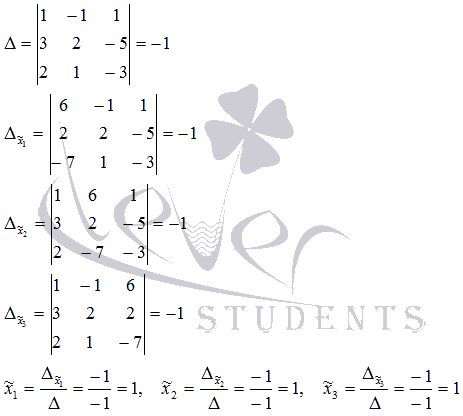
Таким образом, вектор x в базисе 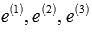имеет координаты .

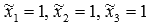Ответ:

.

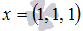18. Прямая на плоскости. Общее уравнение прямой, уравнение прямой с угловым коэффициентом.

Прямая на плоскости

Общее уравнение

Ax + By + C ( 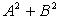> 0).

Вектор 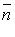= (А; В) - нормальный вектор прямой.

В векторном виде: 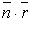+ С = 0, где 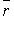- радиус-вектор произвольной точки на прямой (рис. 4.11).

Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Уравнение прямой в отрезках

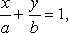
где a, b - величины отрезков, отсекаемых прямой на осях координат.

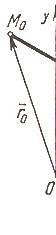
Нормальное уравнение прямой (рис. 4.11)

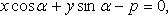
где 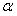- угол, образуемый нормально к прямой и осью Ox; p - расстояние от начала координат до прямой.

Приведение общего уравнения прямой к нормальному виду:

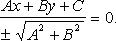
Здесь 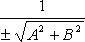- нормируемый множитель прямой; знак выбирается противоположным знаку C, если 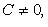и произвольно, если C = 0.