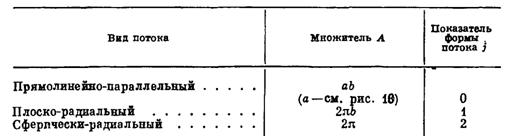
Значения А и j для отдельных видов одномерного потока
Массовый дебит М в уравнении (IV.18), очевидно, содержит тот знак, который имеет производная левой части. По принятому нами в настоящем параграфе условию надо считать, что дебит М положителен, если 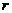 отсчитывается от стока, т. е. галерея или скважина — эксплуатационная; М — отрицателен, если жидкость или газ нагнетаются в пласт. Разделив в (IV.18) переменные и интегрируя, найдем, что
отсчитывается от стока, т. е. галерея или скважина — эксплуатационная; М — отрицателен, если жидкость или газ нагнетаются в пласт. Разделив в (IV.18) переменные и интегрируя, найдем, что
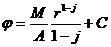 , (IV.19)
, (IV.19)
где С — произвольная постоянная.
Формула (IV.19) даёт общее решение уравнения (IV.18), справедливое при значениях j= 0; 2. При j = 1 (случай плоско-радиального потока) можно условиться, что 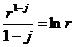 . Тогда мы получим взамен (IV.19) такое выражение для
. Тогда мы получим взамен (IV.19) такое выражение для 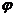 :
:
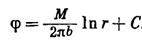
(IV.20)
Это решение есть результат непосредственного интегрирования уравнения (IV.18) при условии, что j = 1. Остаётся найти единственное решение, соответствующее заданным граничным условиям.
Для нахождения единственного решения определим, пользуясь граничными условиями, произвольную постоянную С в равенствах (IV.19) и (IV.20). Здесь могут представиться, например, два ниже следующих варианта задачи.
В одном варианте нам известны: постоянный массовый дебит М и значение потенциальной функции 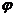 на одной из граничных поверхностей рассматриваемой области пласта, например, на стенке (забое) эксплуатационной скважины или галереи. Пусть на указанной граничной поверхности
на одной из граничных поверхностей рассматриваемой области пласта, например, на стенке (забое) эксплуатационной скважины или галереи. Пусть на указанной граничной поверхности 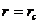 , а
, а 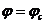 . Подставляя эти значения
. Подставляя эти значения 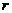 и
и 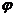 в равенство (IV.19), находим С, после чего решение уравнения (IV.18) получит такой вид:
в равенство (IV.19), находим С, после чего решение уравнения (IV.18) получит такой вид:
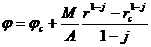 . (IV.21)
. (IV.21)
В другом варианте требуется определить постоянный массовый дебит М, а заданы значения функции 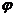 на двух граничных поверхностях пласта, например на стенке (забое) эксплуатационной скважины или галереи и на границе пласта с областью питания.
на двух граничных поверхностях пласта, например на стенке (забое) эксплуатационной скважины или галереи и на границе пласта с областью питания.
Пусть при 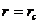 функция
функция 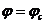 , а при
, а при 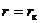 функция
функция 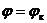 . Подставляя в равенство (IV.19) один раз значения
. Подставляя в равенство (IV.19) один раз значения 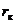 и
и 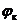 , а другой раз значения
, а другой раз значения 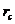 и
и 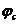 и исключая из двух полученных уравнений постоянную С, найдем массовый дебит М или объёмный дебит
и исключая из двух полученных уравнений постоянную С, найдем массовый дебит М или объёмный дебит 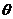 :
:
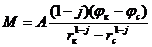 (IV.22)
(IV.22)
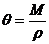
где значения А и j приведены в табл. 1.
Исключая из (IV.21) величину, при помощи формулы (IV.22) получим:
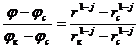 . (IV.23)
. (IV.23)
По формуле (IV.23) можно определять значение функции 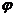 для любой точки пласта с координатой
для любой точки пласта с координатой 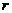 , если дебит М не известен.
, если дебит М не известен.
В случае плоско-радиального потока (j=1) соответственно рассмотренным выше двум вариантам задачи и поставленным граничным условиям получим равенства:
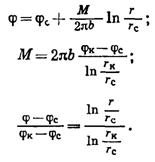 (IV.24)
(IV.24)
(IV.25)
(IV.26)
Итак, формулы (IV.20), (IV.24) — (IV.26) действительны только в случае плоско-радиального потенциального потока любой жидкости. Для всех остальных случаев потенциального одномерного потока имеем формулы (IV.19), (IV.21) — (IV.23).
Заметим, что при рассмотрении в этом параграфе простейших потенциальных одномерных потоков любой жидкости мы фиксировали внимание только на одном отличительном признаке потоков — на их форме (виде); поток характеризовался как бы с геометрической точки зрения. Форма потока нашла своё выражение в показателе j (j = 0; 1; 2). Мы пока не рассматривали вопрос о различиях, которые может внести в существо дела природа самой жидкости. Обобщая решение задачи на все виды жидкости, мы отвлекаемся от ее физических свойств.
