Проницаемость пористой среды
Проницаемость есть свойство пористой среды пропускать через себя жидкость, газ или газожидкостную смесь под воздействием приложенного перепада давления. По отношению к текучей смеси пористая среда является проводником; проницаемость как бы означает проводимость относительно жидкости, газа или газожидкостной смеси.
Познакомимся с параметрами, характеризующими проницаемость. После того как Г. Дарси опытным путем установил закон, носящий его имя, были выполнены многочисленные работы по аналитическому обоснованию этого закона.
В 1930 г. П.Г. Нуттинг ввёл понятие коэффициента проницаемости пористой среды 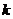 . Коэффициент проницаемости определяется так:
. Коэффициент проницаемости определяется так:
 (II.16)
(II.16)
где  - число Слихтера, являющееся функцией от m – пористости и
- число Слихтера, являющееся функцией от m – пористости и  - некоторого параметра, характеризующего структуру порового пространства.
- некоторого параметра, характеризующего структуру порового пространства.
Таким образом, в случае однородной жидкости коэффициент проницаемости зависит от параметров, характеризующих только пористую среду. Он показывает, как велика способность пористой среды пропускать сквозь себя жидкость и газы.
Поскольку множитель  в формуле (II.16) — безразмерный, коэффициент проницаемости
в формуле (II.16) — безразмерный, коэффициент проницаемости 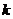 имеет размерность площади, т. е.
имеет размерность площади, т. е.  .
.
Введи обозначение (II.16) в формулы различных теоретических формул, описывающих закон Дарси, получим:  (II.17)
(II.17)
или  , (II.18)
, (II.18)
где 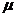 - динамический коэффициент вязкости жидкости.
- динамический коэффициент вязкости жидкости.
Связь между коэффициентом проницаемости 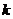 и коэффициентом фильтрации Кф легко установить, приравняв правые части равенств (II.14) и (II.17) или же (II.15) и (II.18). Имеем:
и коэффициентом фильтрации Кф легко установить, приравняв правые части равенств (II.14) и (II.17) или же (II.15) и (II.18). Имеем:  . (II.19)
. (II.19)
За единицу проницаемости пористой среды принимается величина, равная в Международной системе единиц 
 квадратного метра; эта единица называется Дарси. Единица проницаемости Дарси установлена с помощью формулы (II.17), которой, пользуясь соотношением (II.3) можно придать вид
квадратного метра; эта единица называется Дарси. Единица проницаемости Дарси установлена с помощью формулы (II.17), которой, пользуясь соотношением (II.3) можно придать вид  (II.20)
(II.20)
и затем подставить единицу измерения на место каждой величины в её правой части; при этом соблюдено условие, что выбрана некоторая смешанная система единиц. За единицы смешанной системы принимаются: 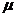 = одному сантипуазу =
= одному сантипуазу =  ;
;  ;
;  ;
;  ;
;  одной технической атмосфере =
одной технической атмосфере = 
Для слабопроницаемых горных пород берут в качестве единицы проницаемости тысячную долю дарси — миллидарси.
Формула (II.20) позволяет определять величину коэффициента проницаемости по данным лабораторных исследований образца породы.
Хотя по определению коэффициент проницаемости не должен зависеть от природы жидкости (т. е. от того, будет ли это вода, нефть, воздух, природный газ и т. д.), опыты указывают на определенное влияние жидкости на результат лабораторных исследований образцов породы на проницаемость. Оказалось, например, что скорость течения дистиллированной воды, нефти и керосина через песчаники со временем уменьшалась. Объясняется это физико-химическим взаимодействием между жидкостью и пористой средой или изменением поперечных сечений поровых каналов вследствие перегруппировки зёрен породы в рыхлых коллекторах. При лабораторных испытаниях образцов породы на проницаемость следует использовать газ, в процессе фильтрации которого не происходит указанных физико-химических взаимодействий.
Коэффициент проницаемости пористой среды 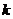 , измеренный в результате опытов по фильтрации однородной жидкости, отличается от значения
, измеренный в результате опытов по фильтрации однородной жидкости, отличается от значения 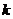 , найденного для той же жидкости, если она движется не одна, а в качестве одной из составляющих фаз неоднородной жидкости (состоящей, например, из нефти и газа или из нефти и воды). То, что в порах породы, кроме данной движущейся жидкости, содержатся и другие фазы — компоненты смеси, коэффициент проницаемости пористой среды для каждого компонента, как правило, полу чается более низкий, чем для однородной жидкости. При фильтрации неоднородной жидкости коэффициент проницаемости среды для её отдельных составляющих фаз называется коэффициентом фазовой проницаемости.
, найденного для той же жидкости, если она движется не одна, а в качестве одной из составляющих фаз неоднородной жидкости (состоящей, например, из нефти и газа или из нефти и воды). То, что в порах породы, кроме данной движущейся жидкости, содержатся и другие фазы — компоненты смеси, коэффициент проницаемости пористой среды для каждого компонента, как правило, полу чается более низкий, чем для однородной жидкости. При фильтрации неоднородной жидкости коэффициент проницаемости среды для её отдельных составляющих фаз называется коэффициентом фазовой проницаемости.
Эксперименты показали (при расчете по закону Дарси), что проницаемость одной и той же пористой среды для воздуха выше, чем для жидкости. Это можно объяснить тем, что закон Дарси в действительности не сохраняется для газов. Было установлено, что этот закон нарушается, если размеры пор становятся сравнимы со средним значением свободного пробега молекул газа или меньшими этого среднего значения.
Ф. Клинкенберг (1941 г.) построил простую капиллярную модель пористых сред и применил теорию проскальзывания Е. Варбурга (1875 г.) к каждому капилляру. Сущность этой теории состоит в том, что у стенок поровых каналов скорость движения слоя газа в отличие от скорости движения жидкости не равна нулю. Поэтому расход газа оказывается большим, чем должен быть по закону Дарси.
Введя поверхностную газопроницаемость  , Клинкенберг определил её из соотношения
, Клинкенберг определил её из соотношения

и исследовал ее зависимость от обратной величины среднего давления Рср. Если проскальзыванием можно объяснить течение газа в пористой среде, то по Клинкенбергу указанная зависимость должна быть линейной:
 , где В и Е – постоянные.
, где В и Е – постоянные.
Поскольку проницаемость пористой среды для газа зависит от средней длины
свободного пробега молекул, она обусловлена давлением, температурой и природой газа.
