Структуре. Уравнение Винера-Хопфа и способ его решения

Определим передаточную функцию линейной системы, отвечающую минимуму дисперсии ошибки на выходе системы

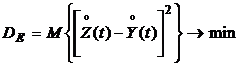. (5.11)

Выразим процесс 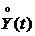в виде (4.4):

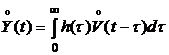. (5.12)

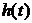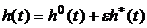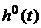Представим в виде суммы , где - переходная функция оптимальной системы. Очевидно, что 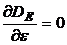при e=0, так как при этом .

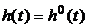Производная 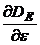определится как:

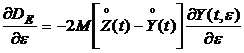, (5.13)

где 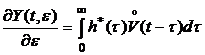. (5.14)

Подставляя (5.14) в (5.13), и приравнивая полученное выражение нулю, будем иметь:

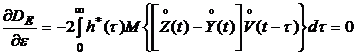. (5.15)

Интеграл (5.15) будет тождественно равен нулю при выполнении условия:

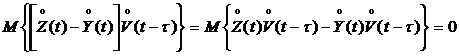. (5.16)

Переписывая (5.16), получим условие, отвечающее минимуму дисперсии ошибки на выходе линейной системы:

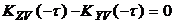или 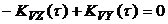. (5.17)

Для решения поставленной задачи перейдем в (5.17) к операторныим спектральным плотностям:

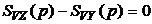. (5.18)

Следует отметить, что уравнение (5.18) справедливо при t>0, так как интеграл в (5.15) брался в пределах 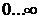. Распространяя уравнение (5.18) на диапазон t<0 и выражая S_VY(p) через S_VV(p), получим:

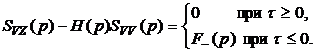. (5.19)

Оригинал, отвечающий правым частям операторных уравнений (5.19), определится как

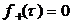при t>0 и 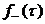при t<0.

В уравнениях (5.19) две неизвестных - 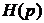и 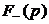. Решение этих уравнений можно получить, разбив их левые части на слагаемые, содержащие, соответственно, только левые и правые полюса. Тогда, приравнивая выражение для левых корней нулю, получим искомое решение

.

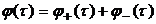При этом

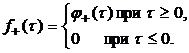
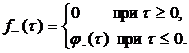
Следовательно изображение искомой функции также может быть представлено в виде суммы:

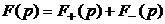. (5.20)

Для выделения составляющих левых частей уравнений (5.19), отвечающих, соответственно, левым и правым корням, произведем факторизацию спектральной плотности суммарного процесса на входе системы:

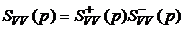. (5.21)

Подставии (5.21) во второе уравнение системы (5.19), получим:

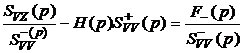. (5.22)

Разобьем первый член уравнения (5.22) на два сумму двух членов, содержащих, соответственно левые и правые корни:

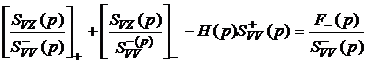. (5.23)

Приравнивая в (5.23) члены, содержащие лишь левые полюса, получим выражение для оптимальной передаточной функции линейной системы:

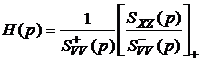. (5.24)

Подставив в (5.24) 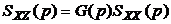, получим окончательное выражение для оптимальной передаточной функции:

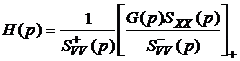, (5.25)

где .

При решении задачи фильтрации помехи (G(p)=1) выражение (5.25) упрощается:

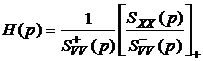. (5.26)

При практическом использовании выражений (5.25) и (5.26) необходимо выделить в выражении 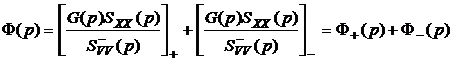слагаемое, содержащее левые корни - 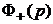. Приведем метод такого выделения. Функция Ф(p) является аналитической в полосе b<Re p<a, ограниченной ближайшими к оси мнимых левым и правым полюсами этой функции (рис.5.2).

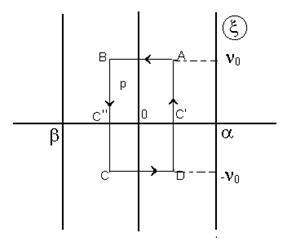
Поэтому, если внутри этой полосы построить прямоугольник АВСD, внутри которого выбрать произвольную точку p,то воспользовавшись интегральной формулой Коши [3], можно записать:

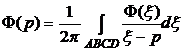или

Рис.5.2

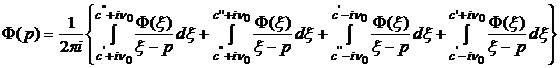. (5.27)

Устремим n₀ к 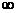и положим, что 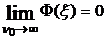. Тогда

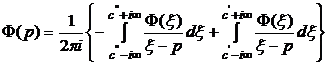. (5.28)

Первое из слагаемых в (5.28) является аналитической функцией в полуплоскости Re p > c^'', второе – аналитической в полуплоскости Re p < c^'. Следовательно, функция Ф(р) является аналитической в полосе b < Re p <a (границы с^' и c^'' могут быть сколь угодно приближены к границам a и b). Последнее обстоятельство позволяет определять Ф₊(р) с помощью теории вычетов:

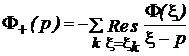, (5.29)

где 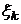- левые полюса .

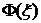Пример. Определим оптимальную передаточную функцию для примера, рассмотренного в предыдущем параграфе:

, , , , .

, , .

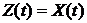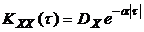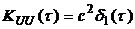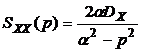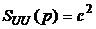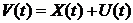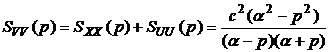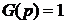Производя факторизацию 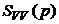, получим ,

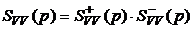где , , .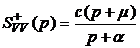

.

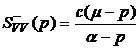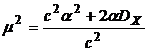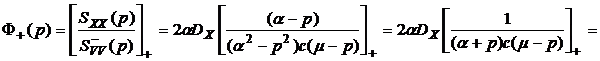
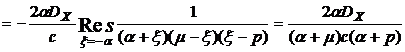
Следовательно передаточная функция оптимального фильтра будет:

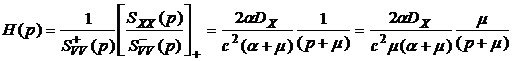. (5.30)

Возможная реализация оптимального фильтра приведена на рис.5.3.

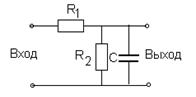Передаточная функция системы рис.5.3 имеет вид

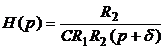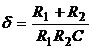, или

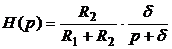. (5.31)

Рис.5.3

Параметры схемы могут быть определены на основе приравнивания правых частей выражений (5.30) и (5.31):

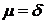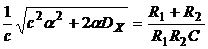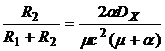® ; (5.32)

Уравнения (5.32) связывают три неизвестные величины: R₁, R₂ и С. Поэтому один из этих параметров контура на рис.5.3 может быть задан произвольно (например, емкость С). Таким образом, оптимальным фильтром при заданных вероятностных характеристиках полезного сигнала и помехи является простейший интегрирующий контур, осуществляющий одновременно операцию умножения на постоянный множитель.