Понятия спектральной плотности
При решении практических задач, связанных с линейным преобразованием стационарных случайных процессов целесообразно пользоваться понятием спектральной плотности или операторной спектральной плотности. Применяя одностороннее преобразование Лапласа, линейную операцию можно записать в виде:
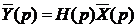 , (4.8)
, (4.8)
где H(p) – передаточная функция линейной системы.
Передаточную функцию можно трактовать как изображение процесса на выходе системы, если на её вход поступает импульсная функция первого порядка 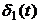 (функция Дирака -
(функция Дирака -  ). Действительно, согласно теореме умножения изображений (теореме Бореля) [2] оригинал выражения (4.8) может быть представлен в виде:
). Действительно, согласно теореме умножения изображений (теореме Бореля) [2] оригинал выражения (4.8) может быть представлен в виде:
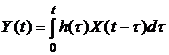 , (4.9)
, (4.9)
где 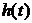 - оригинал H(p).
- оригинал H(p).
Изображение функции Дирака – H(p)=1. Следовательно, изображением процесса на выходе в этом случае согласно (4.8) будет 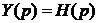 .
.
Получим выражения для определения математического ожидания и корреляционной функции процесса на выходе линейной системы при использовании понятия операторной спектральной плотности процесса на входе.
Выражение (4.9) в случае стационарного процесса на выходе системы можно переписать в виде:
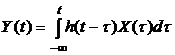 . (4.10)
. (4.10)
Введем в (4.10) новую переменную 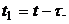 Тогда этот интеграл запишется как:
Тогда этот интеграл запишется как:
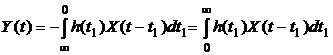 . (4.11)
. (4.11)
Согласно (4.11)
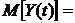
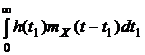 . (4.12)
. (4.12)
В случае стационарного процесса mX=const. Поэтому
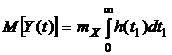 . (4.13)
. (4.13)
Но 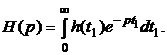 Следовательно
Следовательно 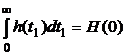 и
и
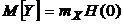 . (4.14)
. (4.14)
Получим выражение для корреляционной функции на выходе линейной системы.
Используя выражение (4.10), будем иметь
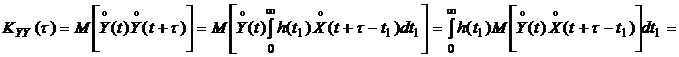
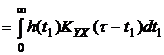 . (4.15)
. (4.15)
Выразим спектральную плотность процесса на выходе системы через взаимную спектральную плотность процессов на выходе и входе системы.
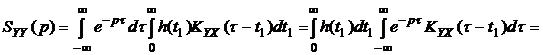
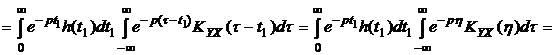
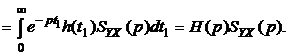 (4.16)
(4.16)
Для того, чтобы получить связь между 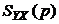 и
и 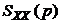 запишем
запишем 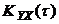 в виде (4.10):
в виде (4.10):
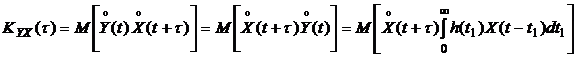 . (4.17)
. (4.17)
Взаимная спектральная плотность 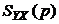 при этом определится как
при этом определится как
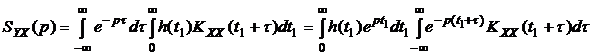 (4.18)
(4.18)
При 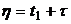
 выражение (4.18) записывается следующим образом:
выражение (4.18) записывается следующим образом:
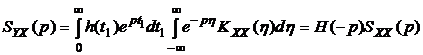 . (4.19)
. (4.19)
Таким образом операторная спектральная плотность процесса на выходе системы определяется как
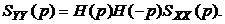 (4.20)
(4.20)
Взаимные операторные спектральные плотности процессов на входе и выходе системы будут:
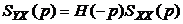 ,
, 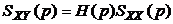 . (4.21)
. (4.21)
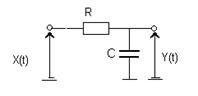
Пример. Определить математическое ожидание и корреляционную функцию процесса на выходе линейной системы, приведенной на рис.4.1, если математическое ожидание процесса на входе 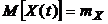 , а корреляционная функция этого процесса
, а корреляционная функция этого процесса 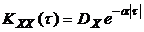 .
.
 Операторная спектральная плотность процесса на входе будет
Операторная спектральная плотность процесса на входе будет 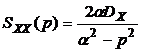 . Рассматривая в контуре рис.4.1. случайный процесс как напряжение, полу
. Рассматривая в контуре рис.4.1. случайный процесс как напряжение, полу
Рис.4.1. чим 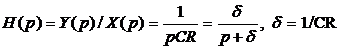 .
.
Следовательно, 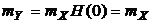 ,
, 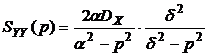 .
.
При t>0 полюса 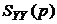 -
- 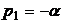 ,
, 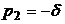 . При t<0 -
. При t<0 - 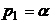 ,
, 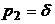 . Используя выражение (3.11) и (3.12), будем иметь:
. Используя выражение (3.11) и (3.12), будем иметь:
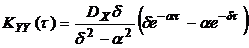 при
при 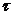 >0,
>0,
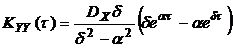 при
при 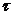 <0.
<0.
Или, объединяя оба выражения, получим
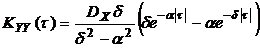 . (4.22)
. (4.22)
ПРИМЕНЕНИЕ ТЕОРИИ СТАЦИОНАРНЫХ ПРОЦЕССОВ К
РЕШЕНИЮ ЗАДАЧ, СВЯЗАННЫХ С АНАЛИЗОМ И
СИНТЕЗОМ ДИНАМИЧЕСКИХ СИСТЕМ
Постановка задачи
Задача анализа является прямой задачей; задача синтеза – обратной.
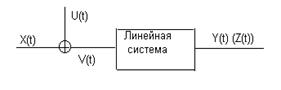 |
Прямая задача. На вход системы поступает не только полезный сигнал X(t), но и помеха U(t) (рис.5.1).
Рис.5.1.
При решении задачи анализа заданы вероятностные характеристики процессов на входе системы (полезного и помехи), а также передаточная функция линейной системы. Требуется определить вероятностные характеристики ошибки на выходе, обусловленной зашумленностью полезного процесса.
Задача синтеза системы может быть решена при двух её постановках.
Во-первых, структура системы может быть задана и требуется определить её параметры, исходя из минимизации ошибки на выходе системы.
Во-вторых, требуется определить саму структуру линейной системы, при которой ошибка на выходе системы будет минимальна.
