Периодограммная оценка спектральной плотности мощности дискретного случайного процесса.

Анализ спектров случайных процессов имеет свои особенности. Во-первых простое вычисление спектра с использованием ДПФ не представляет интереса, так как получается лишь спектр одной случайной реализации процесса. Поэтому для спектрального анализа случайных сигналов необходимо использовать усреднение спектра. Во-вторых, использование среднего значения спектральной плотности сигнала по формуле ДПФ неприемлемо, так как для случайных сигналов с нулевым средним среднее значение спектральной плотности сигнала равно нулю:

.

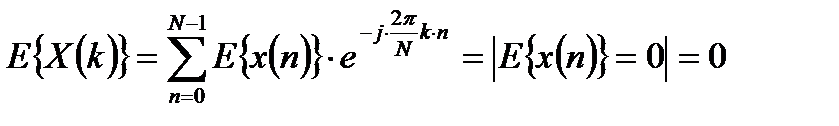Таким образом, усредненное значение спектральной плотности сигнала не несет никакой информации о случайной составляющей случайного процесса. По этой причине при спектральном анализе случайных сигналов рассматривают спектральную плотность мощности (СПМ) случайного процесса.

Спектральная плотность мощности дискретного случайного процесса, полученная с использованием ДПФ, с точностью до несущественного постоянного множителя может быть записана следующим образом:

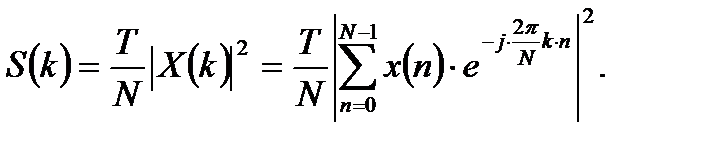(2.1)

После перехода от номера частотного дискрета ДПФ к аргументу частоты можно получить исходную форму периодограммной оценки СПМ:

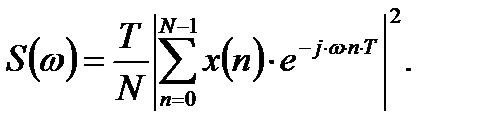(2.2)

Недостатком периодограммной оценки СПМ записанного вида является отсутствие операции усреднения для вычисления математического ожидания. Поэтому полученная периодограмма будет иметь сильно изрезанный вид. Кроме того, дееюдается известное явление «размывания» спектра.

Для усреднения и сглаживания исходной периодограммной оценки известны три метода:

- метод Даньелла;

- метод Барлетта;

- метод Уэлча.

Метод Даньелла основан на усреднении значений СПМ в пределах смежных спектральных частот:

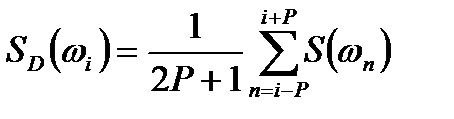, (2.3)

где 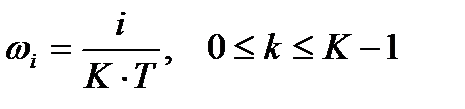- сетка частот;

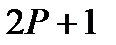- количество точек усреднения;

.

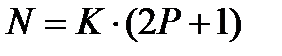Таким образом, происходит уменьшение количества просматриваемых частот от максимального значения 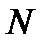к меньшему количеству 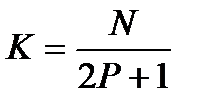за счет объединения соседних частотных дискрет.

В соответствии с методом Барлетта сглаживание обеспечивается за счет усредения значений СПМ, полученных для 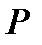коротких неперекрывающихся временных сегментов длительностью :

,

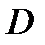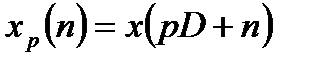где 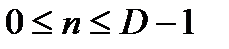- номер отсчета в пределах каждого сегмента.

В сумме все сегменты составляют исходную последовательность длительностью 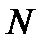. Соответственно, периодограммная оценка по методу Барлетта описывается выражением:

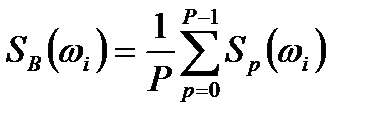, (2.4)

где 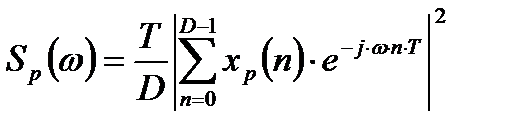- выборочная СПМ.

Периодограмма Уэлча использует модифицированную методику Барлетта за счет применения весовой функции в пределах каждого сегмента и использования перекрывающихся сегментов. Весовая функция ослабляет влияние боковых лепестков за счет некоторого ухудшения разрешающей способности. Перекрытие сегментов позволяет увеличить число усредняемых сегментов и уменьшить результирующую дисперсию оценки СПМ. Уэлчем разработана эффективная вычислительная процедура для реализации метода на основе использования БПФ. Метод Уэлча дееется самым распространенным методом спектрального анализа.

Метод Уэлча организуется следующим образом:

1) Вектор отсчетов сигнала делится на перекрывающиеся сегменты (как правило, перекрытие 50%).

2) Каждый сегмент умножается на используемую весовую функцию.

3) Для взвешенных сегментов вычисляются модифицированные периодограммы (вместо числа отсчетов 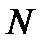в знаменателе используют сумму квадратов модулей коэффициентов окна):

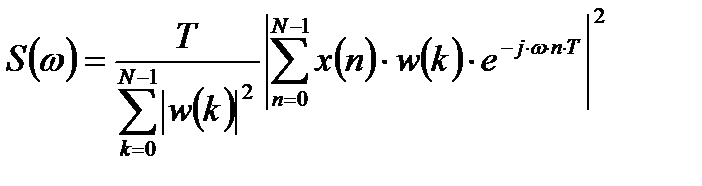. (2.5)

4) Периодограммы всех сегментов усредняются.