ТПС её составные части. История развития

ТПС её составные части. История развития

Последовательность операций по преобразованию сигналов наз. теорией связи. Управление работы железнодорожного транспорта на всех уровнях осуществляется разнообразными в основном электрическими сигналами. Сигналы передаются по проводимым и радиоканалам, а также волоконно-оптическим и др. системам. Рост скорости движения требует повышенной быстродействию систем управления, и скорости передачи информации. Растет также количество и разнообразие использованных систем, передаваемой информации. В них широко используется микроэлектроника и повышенная чувствительность приемных устройств. Одновременно повышается мощность электроустановок, ЛЭП, тяговых сетей, вызывающих помехи и ошибки в каналах передаваемых сигналов. Вследствие этого повышается требование к помехоустойчивости систем передачи и возрастает сложность обработки сигналов при приеме. Для правильного понимания принципов функционирование систем передаваемой информации, способов повышения высоких скоростей и верности передачи, инженеру необходимо знать основные положения теории информации, теории сигналов, теории модуляции, помехоустойчивого кодирования, помехоустойчивого приема.

Цель ТПС - научить принципам построения и работы разнообразных систем управления и связи, а также их функциональных устройств, т.е. фильтров, модемов, кодеков и др. устройств преобразования сигналов используемых на железнодорожном транспорте. ТПС – наука о передачи информации на расстояние. Основа ТПС состоит из:

1) теории информации

2) теории сигналов

3) теории помехоустойчивости.

Задачи теории: Определить как должен работать тот или иной элемент системы связи и каким требованиям он должен удовлетворять. Начало общей теории передачи сообщений было заложено в работе Котельникова “о пропускной способности эфира (радиоканал) и проволоки (связь) в электросвязи” (1933 г), в которой была доказана теорема отсчетов, а в работе Хартли (1928 г) передачи информации, в которой была введена логарифмическая мера информации. В работе Котельникова (1946 г) по теореме информации и по теореме потенциальной помехоустойчивости сформулированы основные положения и теоремы современной ТПС.

Функциональная схема системы связи

К - кодер – устройство для формирования множества кодовых слов;

М – модулятор - устройство, обеспечивающее нанесение информации на переносчик, за счет изменения параметров последнего; Ф – фильтр; Канал передачи информации - совокупность технических средств, обеспечивающих независимую передачу сигналов по линии связи (линия - физическая среда, по которой передаются сигналы). Демодулятор и декодер являются устройствами с противоположными функциями модулятора и кодера. В системах электросвязи это пара проводов, кабель включенный волнооптически или волноводно, в системах радиосвязи в которых распространяются радиоволны от передатчика к приемнику. При передачи сигнала могут и на него воздействуют помехи n(t). Приемник обрабатывает принимаемый сигнал x(t) искаженных помех и восстанавливает по нему принятое сообщение V(t), соответственно U(t) V(t) - U(t). В приемнике выполняются операции обратные осуществленным в передатчике.

В дискретных каналах связи сообщения на входе и выходе представлены в цифровом виде. Такой канал обычно состоит из непрерывного канала, к которому на входе подключаются устройства формирования и кодирования цифровых сигналов, а на выходе решающее устройство, которое служит для опознавания переданных сигналов. Включение решающего устройства в канал вызвано тем, что в результате воздействия помех на выходе канала связи всегда образуется непрерывное множество, даже при дискретном множестве входных сигналов. Решающее устройство необходимо для преобразования непрерывного множества принимаемых сигналов в дискретное множество выходного алфавита канала связи.

Помехи и искажения

Под помехой понимается воздействие накладываемое на сигнал, т.е. помеха это нежелательное изменение сигнала. Шум - случайная помеха. Помехи разнообразны как по своему происхождению так и по физическим свойствам. В радио каналах наиболее распространены атмосферные помехи от грозовых разрядов. Индустриальные помехи возникают из-за резкого изменения тока в цепях электроустройств. В проводных каналах основным видом помех являются импульсные шумы и прерывание связи. Когда помеха влияет на сигнал в виде x = s + n, такая помеха наз. аддитивной. Если же помеха

x = µ(t) s, то называется мультипликативной, n - шум,

µ(t) - случайный процесс. В реальных каналах имеют место обе помехи:

x = µ(t) s + n. Аддитивные делятся:

1) флуктуационные или гладкие

( распределённые по частоте или времени)

2) сосредоточенные по частоте (гармонические)

3) сосредоточенные по времени (импульсные).

Флуктуационный – это непрерывный во времени с гаусовским распределением, мгновенным значениям и нулевым математическим ожиданием. Энергетический спектр такой помехи n0 в пределах анализируемой полосы частот Δf полагают равномерным (помеха типа белого шума) Часто такую помеху полагают стационарной и эргодической. Гармоническая – это аддитивная помеха, энергетический спектр которой сосредоточен в сравнительно узкой полосе частот сопоставимой или даже более узкой, чем полоса сигнала. Импульсная- это аддитивная помеха представляющая собой последовательность импульсов, возбуждаемых кратковременным ЭДС апериодического или колебательного характера. Шум представляет собой случайную помеху. Источниками шума в электрических цепях могут быть флуктуация тока из-за дискретной природы носителей зарядов (электроны, дырки, ионы) - это “дробовой эффект” Наиболее распространенной причиной распространение шума является флуктуации из-за теплового движения носителей заряда в проводнике вызывающие случайную разность потенциалов на его концах. Квадрат эффективного напряжения теплового шума определяется формулой Найквиста: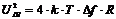

T-абсолютная температура которая имеет сопротивление R, Δf - полоса частот,

В реальном канале сигнал при передачи искажается и сообщение воспроизводится с некоторой ошибкой. Причинами ошибок являются искажения вносимые самим каналом и помехи. Частотные и временные характеристики канала определяют так называемые линейные искажения. Канал может вносить и нелинейные искажения обусловленные нелинейностью его звеньев. Линейные и нелинейные искажения обусловлены известными характеристиками каналов и в принципе могут быть устранены путем соответствующей коррекции. Помехи заранее известны и не могут быть полностью устранены.

8. Сигналы и их спектры (Спектральный анализ сигналов).

Сигналы представляют собой изменяющуюся во времени электрическую величину. Различают сигналы периодические и непериодические. Простейшие непериодические сигналы представляют собой одиночные импульсы произвольной длительности

Рисунок

Периодические - бесконечную временную последовательность импульсов одинаковой формы с равными периодами повторения s(t) = s(t + n T),

n = ± 1, ±2,…, T - период сигнала

Рисунок

Кроме временного, существуют и другие формы представления сигналов. При анализе сигналов и их прохождении по каналу связи удобнее применять частотное представление. Известно, что любую периодическую функцию фремени s(t) с помощью ряда Фурье можно представить в виде суммы гармонических составляющих

s(t) = 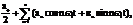где а₀/2 - постоянная составляющая s(t),

a_n, в_n - амплитуды косинусной и синусной составляющих ряда (коэффициенты ряда). Этот ряд может быть преобразован к виду:

s(t) = 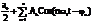где А_n - амплитуды гармонических составляющих ряда

A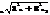

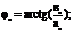
Амплитуды гармонических составляющих могут быть определены с помощью формул Эйлера для коэффициентов ряда Фурье:

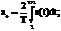
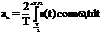; в_{n =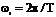} - основная частота последовательности, образующей периодический сигнал на интервале времени 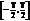. Гармонические составляющие ряда (1) графически представляются отдельными спектральными линиями А_n = f(w), разнесенными относительно начала координат на расстояния nw₁. Совокупность величин An называют спектром амплитуд. Спектр содержит бесконечное число гармоник, амплитуды An которых убывают в пределе до бесконечно малого значения. Спектр - дискретный (линейчатый). Для передачи сигнала без искажений необходимо по каналу связи передать все бесконечное число гармоник. Практически это невозможно, т.к. потребовался бы канал с ¥ большой полосой частот. Допускаются некоторые искажения формы сигнала, что позволяет ограничиться передачей конечного числа гармонических составляющих. Чем больше число гармоник передается, тем меньше искажения. Передают только часть гармоник, несущих основную энергию сигнала. Интервал на шкале частот, в котором размещается ограниченный спектр сигнала, называют шириной спектра. Кроме спектра амплитуд рассматривают также спектр фаз.

Выводы. 1. Спектральное представление сигналов - разложение его на сумму, конечную или бесконечную, элементарных гармонических сигналов с различными частотами. 2. Периодические сигналы можно представить с помощью рядов Фурье, которые образуются суммированием, вообще говоря, бесконечного числа гармоник с частотами, кратными основной частоте повторения последовательности. 3. Спектральное представление непериодических, в частности импульсных, сигналов осуществляется путем разложения их в интеграл Фурье. 4. В частотной области сигнал характеризуется своей спектральной плотностью. 5. Сигнал и его спектральная плотность связаны взаимно парой преобразований Фурье.

9, Спектр периодического сигнала. Ширин а спектра.

Рассмотрим разложение в ряд Фурье периодической последовательности прямоугольных видеоимпульсов с известными параметрами (t, Т, А), четной относительно точки t = 0

Рисунок

В технике связи отношение 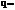называют скважностью последовательности. Для четкой функции коэффициенты ряда Фурье равны ;

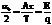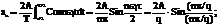
в = 0 отсюда приходим к следующему ряду Фурье

s(t) =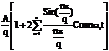

Рисунок

При 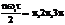и т.д. Sin 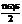обращается в "0" и соответствующие гармоники также будут равны нулю. При 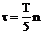обращаются в "0" 5, 10, 15 и т.д. гармоники. Действительно для 5-ой гармоники (n = 5)

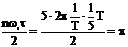a_n=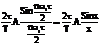

10, Спектр непериодического сигнала. Ширин а спектра. Спектральная плотность. Спектр непериодического сигнала определяют, используя интеграл Фурье 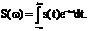Сигнал s(t) и его спектральная плотность S(w) взаимно-однозначно связаны прямым и обратным преобразованием Фурье S(t) =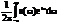 Непериодический сигнал можно рассматривать как периодический с периодом Т . При этом разность частот между соседними гармониками стремиться к нулю. Спектр становится сплошным, амплитуды - бесконечно малыми. Спектральная плотность сигнала S(w) - комплексная величина, ее можно представить в виде

S(w) = A(w) + i B(w) = S(w) e 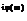, где

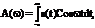
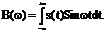
Модуль и фаза спектральной плотности S(w) = 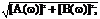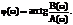Структура спектра непериодического сигнала полностью определяется спектром амплитуд S(w) и спектром фаз 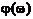(это и есть спектральная плотность).

Спектральная плотность прямоугольного видеоимпульса амплитудой V, длительностью 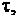симметричного относительно начала отсчета времени: на основании (3)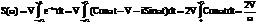

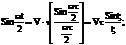где

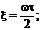
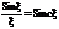координатный синус или функция отсчета. Значение спектральной плотности на нулевой частоте равно площади импульса S(o) = V 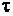. Спектральная плотность обращается в нуль при 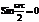или при 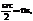где n = 1,2,3…; т.у. при w= 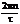.График отсчетной функции Рисунок

Необходимую ширину спектра Dw выбирают предельно малой, но такой, чтобы в ней была сосредоточена основная энергия сигнала (30% в первом лепестке). Энергия может быть определена согласно равенству Парсеваля

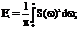
Dw» 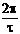; D¦_(Гц)» Этим выражением пользуются для оценки ширины спектра, в общем случае D¦ = , где К - некоторый коэффициент К ³ 1. Короткий импульс имеет широкий спектр , а длинный импульс - узкий спектр. Это общее положение, согласно которому ширина спектра любого процесса обратно пропорциональна его длительности. При t®0 импульс вырождается в дельта - функцию d(t), спектр которой является равномерным (белый шум).

Выводы. (результаты, резюме):1. Спектральное представление сигналов - разложение его на сумму, конечную или бесконечную, элементарных гармонических сигналов с различными частотами. 2. Периодические сигналы можно представить с помощью рядов Фурье, которые образуются суммированием, вообще говоря, бесконечного числа гармоник с частотами, кратными основной частоте повторения последовательности. 3. Спектральное представление непериодических, в частности импульсных, сигналов осуществляется путем разложения их в интеграл Фурье. 4. В частотной области сигнал характеризуется своей спектральной плотностью. 5. Сигнал и его спектральная плотность связаны взаимно парой преобразований Фурье.

11) Спектральный метод исследования прохождения сигналов через линейные цепи.

Под линейностью понимается свойство системы не образовывающее гармонических колебаний на выходе, т.е. на выходе линейной цепи не могут присутствовать гармоники с частотами которых не было на входе если на вход линейного сигнала подать одно гармоническое колебание с известной частотой, амплитудой начальной фазы, то на выход должно быть тоже одно гармоническое колебание той же частоты, но возможно с другой амплитудой и начальной фазой. По изменению амплитуды гармоники можно судить о степени затухания гармонического колебания в этой системе. А по изменению начальной фазы о скорости распространения сигнала в ней. Если для какого-то конкретного сигнала известна функция, показывает изменение затухания и скорости распространения гармоники со всеми возможными частотами, эта функция является адекватной математической модели этой системы в частотной области. Она называется комплексным коэффициентом передачи системы:

К(jω) = | К(jω)| e ^jφ(ω), где

| К(jω)| - АЧХ,

φ(ω) – ФЧХ. АЧХ характеризует передаточное свойство системы по амплитуде, АЧХ показывает для каждого конкретного значения ω_j отношение амплитуды гармоники этой частоты на выходе системы к амплитуде гармоники этой же частоты на входе. Полоса частот в пределах которой АЧХ изменяется от своего максимального значения до 0,707 называется полосой пропускания системы. Если коэффициент передачи системы остается постоянным для всех частот, то такая система считается идеальной и коэффициент передачи становится не функцией частоты, а постоянной коэффициентом усиления/ослабления системы. Данный коэффициент говорит об изменении масштаба сигнала без изменения его формы при прохождении сигнала через эту систему. ФЧХ для каждого конкретного значения ω_j показывает набег фазы гармоники этой частоты за время прохождения через систему. Она характеризует скорость распространения гармоники в системе. Поскольку набег фазы прямо пропорционален значению частоты ω_j

умножению на время распространения гармоники в системе:

φ(ω) = Δt_jω_j. Если скорость распространения гармоник всех частот в системе одинакова, то набег фазы каждой гармоник будет прямо пропорционален значению частоты этой гармоники, т.к. Δt_j=const для всех частот и ФЧХ такой системы будет иметь вид наклонной прямой линии. Чем меньше угол наклона идеальная и реальная ФЧХ относительно оси абсцисс, тем выше скорость распространения гармоник в этой системе. Гармоники более высокой частоты распространяются быстрее в рассматриваемой системе и затухание сильнее по сравнению с НЧ компонентами. Подобные характеристики имеют отрезок телефонного кабеля определенной длины. Суть спектрального метода анализа линейных систем заключается в выражении:

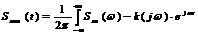
По известному входному сигналу находят с помощью прямого преобразования Фурье его спектральной плотности. Спектр выходного сигнала находят перемножением входного сигнала и комплексного коэффициента передачи системы:

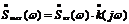
а затем по известному спектру выходного сигнала находят его форму с помощью обратного преобразования Фурье:

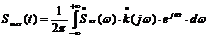
Рисунок

К основным видам аналоговой модуляции относятся: амплитудная (АМ), фазовая (ФМ) и частотная (УМ) модуляция. Разновидностями АМ являются балансная (БМ) и однополосная (ОМ) модуляция. Общее выражение для АМ колебания имеет вид а(t) = А(t) Cos(w₀t + 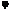₀). Для тональной АМ S(t) = S₀ Cos( 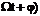и A(t) = A₀ + K _AM × S(t) + A₀ + DAm Cos( 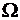t +j), где 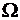- частота модуляции, Кам - коэффициент пропорциональности, DAм = Кам × S₀ - амплитуда изменения огибающей. Отношение М = D A_м/A₀ называется коэффициентом модуляции и характеризует глубину изменения огибающей амплитуд.

Рисунок

Амплитуда колебаний при М £ 1 изменяется от A_min = A₀ (1-M) до А_max = А₀ (1 + М), М = 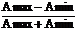. Средняя за период модуляции мощность равна среднему квадрату амплитуды А(t) A²(t) = A²₀(1 + 0,5 M²) = A²₀ 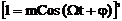пиковая мощность равна 4Р₀, а средняя - 1,5 Р₀. При модуляции одним тоном, когда s(t) = cos Wt

a(t) =A₀(1+M CosWt)Cosw₀t = A₀Cosw₀t + +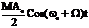

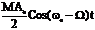+ . Как известно CosL ×Cosb = 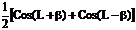. Эта формула определяет спектральный состав одноканального АМ-сигнала, здесь w₀ + W - верхняя боковая частота, w₀ - W - нижняя боковая частота.

Рисунок

Ширина спектра при АМ в два раза шире спектра сообщения F_max; D¦ = 2 F_max.

Возможна балансная АМ с подавлением несущего колебания БМ, а также модуляция с одной боковой полосой частот (ОМ) (ОБП, SSB - Single side bana).Системы БМ и ОМ позволяют сократить бесполезный расход энергии на составляющую несущей частоты, а при ОМ - вдвое сократить ширину спектра передаваемого сигнала.

14, Модулированные колебания. Угловая модуляция. Для передачи информации по каналу связи необходимо иметь переносчик в качестве которого может служить любой физический процесс, протекающий во времени и способный распространяться в пространстве. Переносчиками информации могут быть электромагнитные и звуковые волны, свет (тоже эл.м.в.) В электросвязи в качестве носителя информации используется электрический ток, способный легко распространяться по проводам на большие расстояния. Нанесение информации на переносчик называют модуляцией. В самом общем случае сигнал, несущий в себе информацию, можно представить в виде соотношения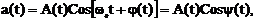

где A - амплитуда, w₀ - частота, j(t) - фаза колебания, y(t) - угол колебания. Различают амплитудную (АМ) и угловую модуляцию (УМ). Сигнал занимает определенный участок электромагнитного спектра Dw. Как правило, выполняется соотношение Dw/w₀ << 1. т.е. любое модулированное колебание есть узкополосный процесс. Спектр речи до 6000 Гц, при несущей 150 кГц Fmax /f₀ = 6 ×10³ /1,5 ×10⁵ = 0,04 << 1, для ТV Fmax = 6 МГц, f₀ ³ 50 МГц, Fmax / f₀ = 0,12 << 1.

Процесс модуляции приводит к сложному преобразованию спектра сигнала. Модуляция приводит к 1) расширению спектра и 2) переносу его в область несущей частоты.

Рисунок

К основным видам аналоговой модуляции относятся: амплитудная (АМ), фазовая (ФМ) и частотная (УМ) модуляция. Разновидностями АМ являются балансная (БМ) и однополосная (ОМ) модуляция.

Угловая модуляция. Сигнал с угловой модуляцией определяется соотношением а(t) = A₀ Cos [w₀t + j(t) ] = A₀ Cos y (t)/ Полная фаза (угол) ВЧ колебания y(t) = w₀t + j(t), а мгновенная частота колебания изменяется по закону производной w (t) = 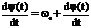. Наоборот, при изменении частоты по закону w(t) , фаза колебания y(t) , будет изменяться по закону интеграла от w(t) y(t) + 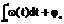. Для фазовой модуляции (ФМ)

y(t) = j₀ + Dj_мS(t) и имеем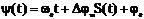

a(t) = A₀Cos[w₀t + Dj_м S(t) +j₀] (ФМ)

При ЧМ по закону передаваемого сообщения изменяется частота несущего колебания 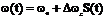, где 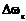- амплитуда частотного отклонения (девиация частоты). Полная фаза колебания при этом будет равна:

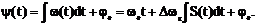
Выражение ЧМ сигнала записывается в виде

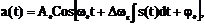(ЧМ)

когда модуляция одним тоном s(t) = CosWt выражения сигнала при ФМ и ЧМ по форме имеют одинаковый вид:

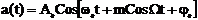ФМ m =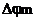

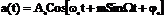индекс угловой модуляции ЧМ m = 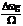Для определения спектра при 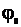= 0 заменим косинус суммы двух углов по известным формулам тригонометрии Cos (L +b) + Cos b CosL- Sinb SinL

a(t) = 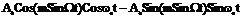. Из теории бесселевых функций известны следующие соотношения

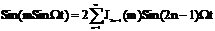
функция Бесселя (порядка) индекса

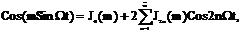
где Jn(m) - бесселева функция первого рода n-го порядка от аргумента m

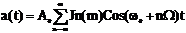более компактный вид. Окончательно получим: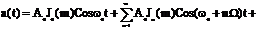

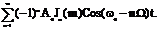+ Даже при синусоидальных ЧМ и ФМ получается теоретически безграничный спектр.

Он состоит из несущей и двух боковых полос ( 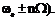Амплитуда несущей А₀ J₀ (m) при ЧМ и ФМ (в отличие от АМ) зависит от модулирующего колебания. При значениях m = 2,3; 5,4 и др. J₀ вообще будет равна нулю. Амплитуда боковых частот равна 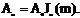Практически же ширина спектров ЧМ и ФМ сигналов ограничена.

Рисунок

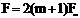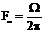Амплитуды боковых частот быстро убывают с увеличением номера гармоники n. При n > m составляющие спектра малы и ими можно пренебречь. Практически ширина спектра при угловой модуляции равны ,где - частота модулирующего колебания. Различие между ЧМ и ФМ проявляется только при изменении частоты модуляции W. При УМ m = ( 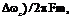поэтому при m >> 1 полоса 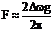практически не зависит от частоты модулирующего колебания F_m.

При ФМ m = 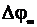и m >> 1 ширина спектра будет равна 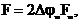т.е. она зависит от модулирующей частоты. В этом и состоит различие в спектрах УМ и ФМ. В ЧМ девиация 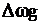пропорциональна амплитуде НЧ сигнала и не зависит от частоты модулирующего колебания Fm. При ФМ ее индекс

m = Dj_m пропорционален амплитуде НЧ сигнала независимо от его частоты, поэтому девиация частоты при ФМ линейно увеличивается с ростом частоты W (Fm).

Рисунок

Кроме структуры колебания УМ и ФМ различаются и способом осуществления. При УМ обычно применяют прямое воздействие на частоту автогенератора. При ФМ генератор имеет стабильную частоту, а фаза колебания моделируется в одном из последующих элементов устройства.

15. Дискретная модуляция часто называется манипуляцией. Устройство осуществляющее дискретную модуляцию называют манипулятором или генератором сигналов. При АМ_Н символу 1 соответствуют передача несущей в течение времени t₀ (посылка, символу 0 - отсутствие колебания (пауза).

Рисунок

При ЧМ_Н несущей с f₁ соответствует символ 1, f₀ - символ "0". При ФМ_Н фаза несущей меняется на 180⁰ при каждом переходе от 1 к 0 и от 0 к 1.

При ОФМ_Н фаза несущей изменяется на 180⁰ при передаче "1" и остается неизменной при передаче "0" (или наоборот). При импульсной модуляции переносчиком информации служит периодическая последовательность импульсов одинаковой формы. При АНМ изменяется амплитуда импульса

A(t) = A₀ + DAs(t). При ШИМ изменяется длительность импульса 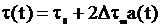где 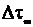- максимальное отклонение импульса в одну сторону. При ЧИМ изменяется частота следования импульсов. При ФИМ - сдвиг импульсов относительно тактовых точек 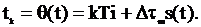Ширина спектра последовательности импульсов практически не зависит от частоты повторения 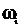и определяется шириной спектра одного импульса. Поэтому рабочая полоса частот, занимаемая импульсными сигналами, практически не зависит от вида модуляции и определяется длительностью и формой импульса. В теории связи вводится понятие базы сигнала 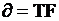- его спектральная полоса для простых сигналов 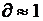, для сложных 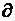>>1. На практике нашли применение шумоподобные сигналы (не являющиеся случайными), сформированные по определенному алгоритму. Эти сигналы относятся к типу широкополосных (ТF >> 1). Относят псевдослучайные м - последовательности Хаффмена, коды Баркера, сигналы Пэли-Плоткина. При НКМ передача отдельных значений сигнала сводится к передаче определенных групп импульсов друг за другом через относительно большие промежутки времени по сравнению с t отдельных импульсов.

16. Помехоустойчивость системы связи. Оптимальный фильтр.

Обычно способ передачи (т.е. способ кодирования и модуляции) задан и нужно определить помехоустойчивость, которую обеспечивают различные способы приема. Возникает вопрос - какой из возможных способов приема является оптимальным? Указанные вопросы являются предметом рассмотрения теории помехоустойчивости, основы которой разработаны акад. В.А. Котельниковым. Помехоустойчивостью системы связи называется способность системы противостоять вредному действию помех и различать (восстанавливать) сигналы с заданной достоверностью. Задача определения помехоустойчивости всей системы в целом весьма сложна. Поэтому часто определяют помехоустойчивость отдельных звеньев системы: 1) приемника при заданном способе передачи, 2) системы модуляции при заданном способе приема и т.д. Предельно достижимая помехоустойчивость называется, по Котельникову, потенциальной помехоустойчивостью. Сравнение потенциальной и реальной помехоустойчивости позволяет дать оценку качества реального устройства и найти еще неиспользованные резервы. Например, зная потенциальную помехоустойчивость приемника, можно судить, насколько близка к ней реальная помехоустойчивость существующих способов приема и насколько целесообразно их дальнейшее усовершенствование при заданном способе передачи. Сведения о потенциальной помехоустойчивости приемника при различных способах передачи позволяют сравнивать эти способы передачи между собой и указать, какие из них являются наиболее совершенными.

Обеспечение высокой помехоустойчивости систем связи осуществляется в принципе двумя путями: а) можно совершенствовать структуру передаваемых сигналов (например, широкополосные сигналы типа кода Баркера; б) создание устройств для обработки, которые наилучшим образом выделяют сигнал, искаженный присутствием шума.

Частотно-избирательная система, выполняющая обработку суммы сигнала и шума некоторым наилучшим образом, называется оптимальным фильтром. На протяжении длительного периода развития техники связи к частотным фильтрам предъявлялось требование возможно более равномерного пропускания спектра сигнала и более полного подавления частот вне этого спектра. Идеальным считался фильтр с прямоугольной П-образной АЧХ. С развитием теории помехоустойчивости существенно изменились трактовка функций линейного фильтра и подход к его настроению. Фильтр с П-образной АЧХ не является оптимальным в тех случаях, когда имеется априорная информация о форме сигнала и характеристиках помехи. В зависимости от решаемой задачи - 1) обнаружены сигнала, 2) измерение его параметров, 3) разрешение (т.е. различение) сигналов - критерии оптимальности могут быть разными. Для задач обнаружения сигналов заданной (т.е. известной) формы в шумах наибольшее распространение получил критерий максимума отношения сигнал/помеха на выходе фильтра.

Квазиоптимальные фильтры

В ряде случаев удаётся получить достаточно эффективную фильтрацию сигналов из смеси с “белым ” шумом применив фильтры более простой конструкции по сравнению с оптимальными фильтрами. Рассмотрим RC 4-х полюсник, интегрирующего типа.

t_ц=R×C – постоянная времени. На входе одновременно действует “белый” шум. Поскольку данная цепь линейна, то прохождение сигнала и шума можно рассмотреть независимо. Максимальная полезность сигнала на выходе достигается в момент окончания импульса.

Отсюда максимальное отношение на выходе цепи:

Э=Е²×t_и - энергия сигнала, В²/Гц. Приняв во внимание, что энергия видеоимпульсов, получим:

Множитель в [ ] даёт величину проигрыша в отношении сигнал/шум по сравнению с оптимальным фильтром. Введя параметр

х=t /R×C=t /t_ц, получаем:

Из графика видно, что при х = 1,25 функция достигает максимума. Выбираем соответствующее значение постоянной времени RC цепи, можно создать весьма простой квазиоптимальный фильтр (почти оптимальный)

Отношение сигнал/шум, который лишь на 11% меньше чем в согласованном фильтре.

Квазиоптимальные фильтры с приёмными характеристиками удается создать только для относительно простых сигналов. Требования: пропустить без ослабления колебания из той области частот где сосредоточена основная доля энергии сигнала.

Теорема Котельникова

Реальные сигналы всегда имеют конечную длительность ограниченную полосу частот. Граничные частоты спектра определяются свойствами системы передачи и самим получателем. Например, при передачи дискретных сообщений полоса частот определяется скоростью передачи, а при передачи телевизионных изображений принятым стандартом четкости (числом строк). Для функции с ограниченным спектром В. А. Котельников доказал теорему лежащую в основе дискретизации непрерывных сигналов. Согласно этой теореме функция U(t), не содержащая частот выше F полностью определяется последовательностью своих отсчетов в моменты времени, отстоящие друг от друга на Δt≤1/2F. Восстановление осуществляется с помощью ряда Котельникова:

Выражение представляет разложение непрерывной функции U(t) в ряд по ортогональным функциям вида (sinx / x). Выражение U(kΔt), называется отсчетами функции U(t), а множитель называется функцией отсчетов. Если обозначим

τ = (t - kΔt), то множитель:

Функция ψ(τ)=1 в моменты времени t = kΔt и ψ(τ)=0, при

t = (k ± m)Δt, где m=1,2,3… Эта функция называется функцией отсчетов или координатным синусом. Ширина главного лепестка на нулевом уровне равна 1/F. Спектр функции отсчетов является равномерным в полосе (-F; F) и равен нулю вне этой полосы. Амплитуда спектра (модуль) S(f)=1/2F. Теорема Котельникова позволяет единым образом рассматривать передачу любого сигнала ( и дискретного и непрерывного) на передачу чисел. Эта теорема лежит в основе всех видов импульсной модуляции. Согласно этой теореме необходимая частота следования импульсов, называемая тактовой частотой F_i должна определяться из условия F_i≥2 F_в ,где F_в – верхняя граничная частота спектра передаваемого сообщения.

22. Принцип цифровой обработки сигналов. Переход к системам цифровой обработки сигналов является одной из основных тенденций современной техники связи. Это направление оказывает влияние на развитие теории и техники сигналов и систем.

Функциональная схема цифровой обработки континуального (непрерывного) сигнала.

Рис