Экстремум функции. необходимое условие экстремума.

Определение. Точка х₀ называется точкой локального максимума(минимума) если существует окрестность Оd(х₀) такая, что f(x)<=f(x₀) (f(x)>=f(x₀)) при всех хÎ Оd(х₀)

Значение f(x₀) – локальный максимум(минимум). Точки локальных максимумов(минимумов) называются экстремумами функций.

Необходимое условие существования экстремума.

Если в точке х₀ f(x) достигает экстремума, то ее производная в этой точке равна 0 (или не существует).

Дано: в точке х₀ f(x) имеет локальный максимум.

Доказать: в этой точке f’(x)=0 или не существует

Доказательство.

Если в точке х₀ – локальный максимум, то существует Оd(х₀) , что f(x)<=f(x₀) для всех хÎ Оd(х₀).

Выберем Dх так чтобы х₀+Dх Î Оd(х₀).

Тогда Dу=f(х₀+Dх)-f(х₀) <= 0при любом Dх.

Тогда f’(x₀) = lim_Dx->0Dy/Dx

Если Dx>0, то lim_Dx->0+0Dy/Dx = f’(x₀+0)<=0

Если Dx<0, то lim_Dx->0-0Dy/Dx = f’(x₀-0)>=0

Если производная существует, то это возможно, когда f’(x₀+0)= f’(x₀-0)

ð f’(x₀)=0

если эти односторонние пределы отличны от 0, то производная не существует.

Точки, в которых производная не существует – критические точки.

Критические точки, в которых производная равна - - стационарные точки.

Критические точки называются точками, подозрительными на экстремум. Это условие явл необходимым, но не достаточным.

ЭКСТРЕМУМ ФУНКЦИИ. ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА.

Пусть х₀ – критическая точка ф-ии y=f(x) непрерывной

Если при переходе через эту точку, производная ф-ии меняет знак с – на +, то в этой точке находится локальный минимум, если с + на - , то локальный максимум. Если же производная не меняет знака, то в точке х₀ экстремума нет.

Док-во.

Пуст в точке x₀-Dx f’(x)<0

X₀+Dx f’(x)>0 (с – на +) 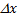>0

Тогда в точке x₀-Dx ф-я убывает и f(x₀)<f(x₀-Dx )

В точке X₀+Dx f’(X₀+Dx)>0 и ф-я возрастает, т.е. f’(X₀+Dx)>f(x₀)

ð X₀ – точка локального минимума

ЭКСТРЕМУМ ФУНКЦИИ. ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА.

Пусть х₀ – стационарная точка ф-ии y=f(x) т.е. f’(x₀)=0

Тогда, если f”(x₀)>0, то x₀ – точка локального минимума. F”(x₀⁾<0, - точка локального максимума.

Доказательство.

Если f”(x₀)>0, то f’(x) возрастает в Оd(х₀) и при переходе черех точку х₀ меняет знак с – на +. Значит х₀ – локальный минимум.

ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ГРАФИКА ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА.

Определение. График дифференцируемой ф-ии y=f(x) называется выпусклым вниз (вогнутым) на интервале (a,b) , если для любого x, принадлежащего этому интервалу, касательная, проведенная к графику ф-ии в этой точке, лежит ниже графика этой ф-ии. Аналогично, график ф-ии называется выпуклым вверх в этом интервале, если для любого х, принадлежащего интервалу, касательная к графику ф-ии , проведенная в точке х, лежит выше графика ф-ии. Точка М₀(x₀,f(x₀)) графика ф-ии, в которой хар-р выпуклости меняется на противоположный, называется точкой перегиба.

Теорема.

Если ф-я y=f(x) дважды дифференцируема в интервале (a,b) и f”(x)>0 в этом интервале, то график этой ф-ии выпуклый вниз в этом интервале. Если f”(x)<0 в этом интервале, то выпуклый вверх.

Теорема.

Пусть для ф-ии y=f(x) , определенной в точке х₀ вторая производная без знака и при переходе через эту точку f”(x) меняет знак, то эта точка – точка перегиба графика ф-ии.

АССИМПТОТЫ ГРАФИКА ФУНКЦИИ.

ассимптоты бывают 2х видов – вертикальные и наклонные.

Определение. Прямая x=x₀ называется вертикальной ассимптотой графика ф-ии y=f(x) если хотя бы один из односторонних пределов ф-ии f(x) в точке x₀ равен +(-) бесконечность.

Ясно, что непрерывная на всей оси ф-я вертикальных ассимптот не имеет.

Определение. Прямая y=kx+b называется наклонной ассимптотой (при к=0 – горизонтальной) графика ф-ии y=f(x) при x стремящемся к +(-) бесконечности, если ф-ию f(x) можно представить в виде:

F(x) = kx + b + a(x), где a(x) стремится к 0 при х стремящемся к +(-) бесконечности.

Если такое представление возможно только при х стремящемся к +бесконечности, то соответствующая наклонная ассимптота называется правой (-бесконечности – левой).

Теорема.

Для того, чтобы график ф-ии y=f(x) имел наклонную ассимптоту y=kx+b необходимо и достаточно чтобы существовали конечные пределы.

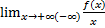= k

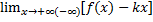И = b

ФОРМУЛА ТЕЙЛОРА.