В цилиндрических координатах

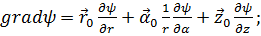(6.14)

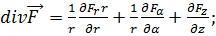(6.15)

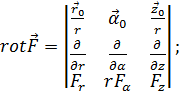(6.16)

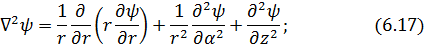
В сферических координатах

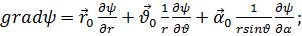(6.18)

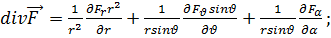(6.19)

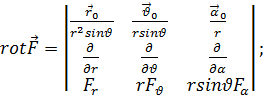(6.20)

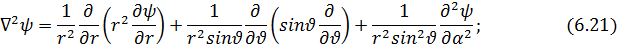
7. О дифференциальных уравнениях
с частными производными

7.1 Уравнения Лапласа и Пуассона.Одним из важнейших средств математической физики является описание процессов при помощи дифференциальных уравнений с частными производными.В отличие от обыкновенных дифференциальных уравнений,содержащих функции одной переменной, в эти уравнения входят функции нескольких переменных. Теория их составляет обширную и сложную область математики, представление о которой невозможно дать в нескольких словах. Однако нельзя пройти мимо того факта, что именно в виде уравнений с частными производными формулируются основные законы электромагнетизма, знакомство с которыми начинается уже в первой главе книги [1].Поэтому ниже излагаются некоторые предварительные сведения о дифференциальных уравнениях математической физики с частными производными.

К распространенным уравнениям математической физики можно придти непосредственно от операций векторного анализа. Так, взяв оператор Лапласа, запишем равенство

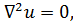(7.1)

где и - некоторая неизвестная функция пространственных координат. Это уравнение Лапласа. В декартовых координатах (7.1) следует записать как уравнение с частными производными:

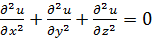(7.2)

В том случае, когда решение и заведомо не зависит от каких-то двух переменных из трёх (скажем, от уи z), уравнение Лапласа (7.2) переходит в обыкновенное дифференциальное уравнение

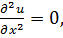(7.3)

общее решение которого очевидно:

и= Ах + В, (7.4)

(А и В - постоянные). Наличие неопределённых констант, т. е. неопределённость самого решения (7.4), можно истолковать как следствие того факта, что исходное уравнение (7.3) не выражает конкретно очерченной задачи. Такая задача появляется, когда уравнение рассматривается при некоторых дополнительных условиях. Пусть, например, решение уравнения (7.3) ищется в интервале 0 < х < а при следующих условиях:

и(0) = 0 и и(а) = и_а.

Вместе с этими условиями уравнение (7.3) составляет так называемую граничную задачу,имеющую единственное решение

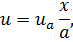
легко получаемое из решения (7.4).

Возвращаясь к уравнению Лапласа (7.1), подчеркнём, что его решение в несравненно более высокой степени неопределённо, чем решение уравнения (7.3). В отличие от обыкновенных дифференциальных уравнений, когда общее решение можно выразить в виде некоторой функции, решения уравнений с частными производными вообще образуют множества («классы») функций. Так всякая функция u, удовлетворяющая в некоторой области V уравнению Лапласа (7.1), называется гармоническойв этой области. Если требуется найти и как решение уравнения (7.1) в области V, на границе которой (поверхности S)задана сама функция и или, например, её производная du/dn (возможны и иные граничные условия),то говорят, что поставлена граничная задача для уравненияЛапласа; употребляются также выражения краевые условия, краевая задача.

Уравнение Лапласа, как говорят, является однородным. Соответствующее неоднородноеуравнение получаем, записав справа в (7.1) вместо нуля заданнуюфункцию f:

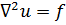(7.5)

Это так называемое уравнение Пуассона.

7.2. Другие уравнения.Следующее однородное уравнение

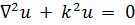(7.6)

известно под названием уравнения Гельмгольца,или уравнения колебаний.Здесь k² - постоянная, роль которой в разных случаях различна.

Возьмём случай, в котором ввиду независимости и от уи z уравнение Гельмгольца переходит в известное обыкновенное дифференциальное уравнение

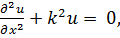(7.7)

общее решение которого может быть записано в следующихдвух формах:

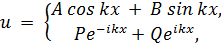(7.8)

где А, В и Р, Q - константы.

Пусть поставлена граничная задача для уравнения (7.7) наотрезке 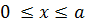с условиями:

u(0) = 0 и u(а) = 0.

В соответствии с первым граничным условием, мы должны положить в (7.8) А = 0, а согласно второму должно быть ka = mπ (m = 1, 2, 3, ...). Поэтому граничная задача имеет следующее множество решений:

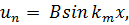
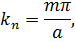
причём m = 1, 2, 3, ....; (7.9) .

Kаждое решение реализуется при вполне определенном значении постоянной k. Говорят, что решения и_m образуют систему собственных функцийданной задачи, а k_m называются соответствующими им собственными значениями.

Записывая справа в (7.6) вместо нуля заданную функцию f, получаем отвечающее уравнению Гельмгольца неоднородное уравнение

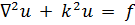(7.10)

(неоднородное уравнение Гельмгольца).Обычно решения однородного уравнения (7.6) описывают «свободные» (совершающиеся без внешних воздействий) колебания различных систем, а решения неоднородного уравнения (7.10) - «вынужденные» колебания; функция f выражает при этом внешнее воздействие, «вынуждающую силу».

Далее напишем однородное волновое уравнение

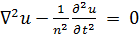(7.11)

и соответствующее неоднородное уравнение

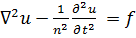, (7.12)

называемое уравнением Даламбера. Решение и есть функция координат и времени. Функция f, как и ранее, выражает «вынуждающую силу».

В дальнейшем мы вернемся к обсуждению записанных здесь уравнений математической физики и выясним их роль в теории электромагнетизма. Встретятся и различные уравнения с частными производными относительно векторных функций и, в частности, уравнения типа (7.1), (7.5), (7.6), (7.10) - (7.12).

7.3. Понятие линейности. Обозначив в (7.1) и (7.5) 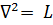, в (7.6) и (7.10) 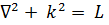ив (7.11) и (7.12) 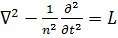, запишем следующие легко проверяемые равенства:

L(cu) = cLu,

L(u₁ + u₂)= Lu₁ + Lu₂ (7.13)

Здесь L понимают как оператор указанного вида, действующий на некоторую функцию, стоящую за ним справа; с - константа. Равенства (7.13), как принято говорить, выражают свойства линейности рассматриваемых уравнений математической физики.

Согласно (7.13) линейность однородных уравнений (7.1), (7.6), (7.11) означает, что если u₁, и₂, u₃, … - решения какого-нибудь из них, то и линейная комбинация

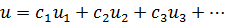
(с₁, c₂, с_з, ... - произвольные константы) - также есть решение данного уравнения.

Линейность неоднородных уравнений (7.5), (7.10), (7.12) проявляется в следующем. Пусть f₁, f₂, f_з, … - различные правые части одного из этих уравнений, при которых оно имеет решения и₁, и₂, и₃, …. Тогда линейная комбинация c₁u₁ + с₂и₂ + с₃ и₃ + … есть решение данного уравнения, в правой части которого стоит аналогичная линейная комбинация (те же константы) соответствующих правых частей:

c₁f₁ + с₂f₂ + с₃ f₃ + ... .

Линейность рассмотренных уравнений отвечает имеющему большое значение в физике принципу суперпозиции (принципу наложения).