Теорема Бетти. Теорема Максвелла.

А) - прогиб (линейное перемещение);

- i – показывает направление перемещения от действия силы;

j – номер силы, вызвавшей это перемещение.

- работа силы на перемещении по ее направлению от действия силы . Т.к. к моменту начала действия силы уже исчерпана и остается постоянной по величине, то перед этим слагаемым нет коэффициента .

Б)

Приравняем (*) и (**):

Теорема Бетти – теорема о взаимности работ.

Работа I силы на перемещении по её направлению от действия II силы равна работе II силы на перемещении по ее направлению от действия I силы.

Если P₁ и P₂ – единичные силы.

Перемещение точки приложения точка P₁ в направлении ее действии, вызвавшее силой P₂ равно перемещению точки приложения; точка P₂ в направлении ее действии, вызвавшее действительные силы P₂.

Теорема Кастилиано.

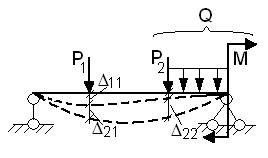
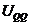- энергия, накопленная в результате деформации системы только силами Q и численно равная работе сил Q на вызванных ими перемещениях.

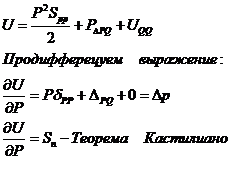
Так как частное произведение от потенциала энергии деформации, взятая по одной из внешних сил равно перемещению точки приложения этой силы в направлении ее действия.

Если частное произведение берется по силе - получается прогиб, если по моменту – угол поворота сечения.

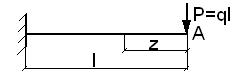
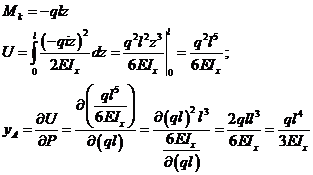
Интеграл Мора.

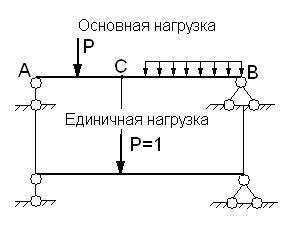
Примем следующие нагружения балки. Сначала приложим силу P₁, затем нагрузим. Определим работу постоянной по величине единичной силы на перемещении по направлению её действия от заданной нагрузки.

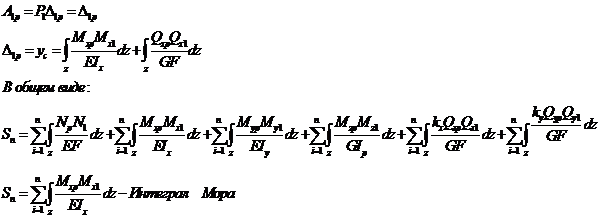
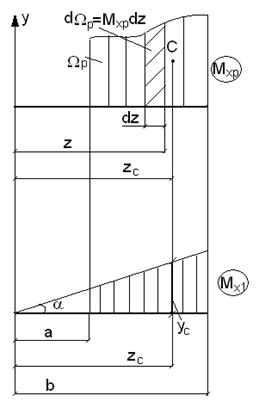
Правило Верещагина.

Правило Верещагина – графическое выражение интеграла Мора, применимо для стержней с прямолинейной осью. При приложении единичной нагрузки к прямолинейной оси, единичная эпюра всегда линейна (треугольник или прямоугольник).

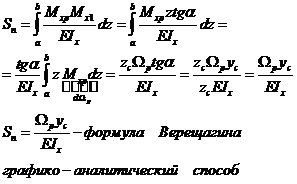
Глава 11.

Статически неопределимые системы.

Статическая неопределимость.

Статически неопределимой называется система, в которой число неизвестных (опорные реакции, реакции связи) больше основных уравнений равновесия.

Связи, накладываемые на систему сверх основных связей равновесия, называются дополнительными. Они определяются из дополнительных уравнений совместности деформаций. Число этих уравнений равно числу статической неопределимости системы.

Статическая неопределимость внешним образом:

Система 1 раз статически неопределима.

5 неизв.-3 уравнения равновесия=2 раза статически неопределима.

5 раз статически неопределима.

Статическая неопределимость внутренним образом.

3 раза статически неопределим любой замкнутый контур независимо от формы.

Система 2 раза статически неопределима.

Система 3 раза статически неопределима.

Плоский шарнир снимает (п-1) степеней статической неопределимости при сходящихся в нем п-стержней.