Линейные операции над случайными процессами

С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ

Свойства корреляционных функций случайных процессов

С непрерывным временем.

В этом разделе мы подробно изучим введенную в п.п. 1.1 корреляционную функцию случайных процессов 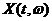. Напомним, что корреляционная функция случайного процесса – это функция двух аргументов :

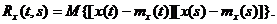(4.1)

На практике часто используют нормированную корреляционную функцию

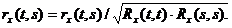(4.2)

Последняя функция удобна тем, что ее значения находятся в пределах ± 1 и, следовательно, по абсолютной величине 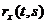можно судить о степени связности (зависимости) двух ординат случайного процесса.

Непосредственно из определения корреляционной функции (4.1) следует, что корреляционная функция симметрична

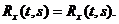(4.3)

Это обстоятельство позволяет ограничиться областью аргументов t≥ s или s ≥ t. Корреляционная функция случайного процесса удовлетворяет неравенству

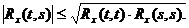(4.4)

Корреляционная функция обладает очень важным свойством, позволяющим существенно облегчить анализ случайных процессов, свойством положительной определенности [6 ]. Смысл этого свойства в следующем. Рассмотрим интеграл

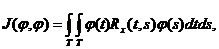(4.5)

где 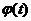- некоторые произвольные функции.

Подставив в (4.5) выражение корреляционной функции (4.1), меняя местами операции интегрирования и математического ожидания, получим

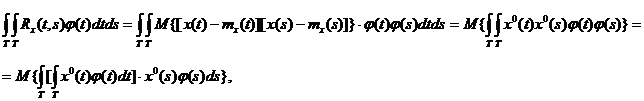где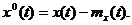

Последнее выражение можно записать теперь в виде:

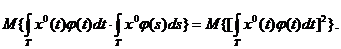
Но математическое ожидание неотрицательной величины не может быть отрицательным и, следовательно, при любой области интегрирования Т и при любой функции 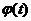интеграл (4.5) не меньше нуля. Функция 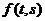, обладающие таким свойством, называются положительно определенными функциями.

Сложение случайных процессов.

Рассмотрим сумму двух случайных процессов, зависящих от одного и того же аргумента t:

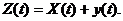( 4.6 )

Найдя математическое ожидание и корреляционную функцию случайного процесса 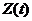, полагая, что корреляционные функции и математические ожидания процессов 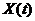и 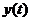известны. По теореме сложения математических ожиданий [ 1 ] имеем

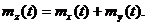
( 4.7 )

По определению корреляционная функция 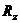( t, s ) равна

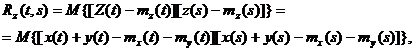
или

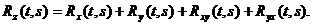( 4.8 )

В общем случае при суммировании произвольного числа случайных функций x_i (t) с весами a_i имеем

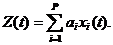( 4.9 )

Математическое ожидание Z (t) равно

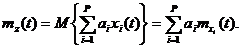( 4.10 )

Корреляционная функция R_z ( t, s ) определяется из выражения

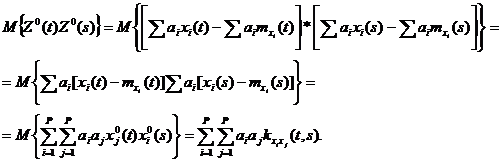( 4.11 )

Сумма в этой формуле содержит корреляционные функции R _{i i} ( t, s ) и все возможные взаимные корреляционные функции.

Дифференцируемость выборочных функций случайного

Процесса

Для доказательства ряда теорем, связанных со свойствами случайных функций, нам необходимо определить среднеквадратической сходимости [ 1].

Определение 4.1.

Последовательность случайных величин x_1, x_2, … x_n сходится в среднеквадратическом, если

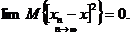(4.12)

Случайную величину x называют пределом в среднеквадратической последовательности случайных величин x_1, x _2, … x_n и пишут

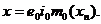
Среднеквадратическая сходимость обладает следующими свойствами.

Свойство 1. Если {x_n},{x_m} – последовательности случайных перемен-ных, такие, что М { (x_n-x_m)² }→ 0 при ( m – n ) → 0, то существует х такое, что x _n → х в среднеквадратическом при n→ ∞

Свойство 2. Пусть {x_n} – последовательность случайных переменных. Предположим, что М { x_n² } < ∞ и x _n → х в среднеквадратическом при n→ ∞.

Тогда

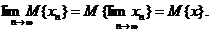
Свойство 3 Пусть x _n → х, y _n → y в среднеквадратическом и М

{ x_n² } < ∞ и

М { y ² } < ∞, тогда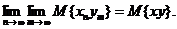

Введем теперь определение непрерывности случайного процесса.

Определение 4.2.

Случайный процесс 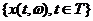второго порядка непрерывен по t в среднеквадратическом, если

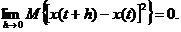
(4.13)

Следующая теорема дает удобный критерий определения непрерывности случайных процессов.

Теорема 4.1.

Случайный процесс 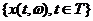второго порядка непрерывен в среднеквадратическом для 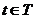тогда и только тогда, когда функция 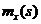непрерывна по 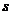и корреляционная функция 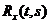непрерывна на диагонали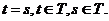

Доказательство.

Имеем

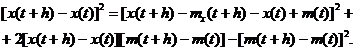(4.14)

Возьмем математическое ожидание от обеих частей и найдем

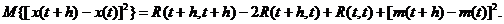
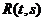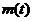Если и - непрерывные функции, то

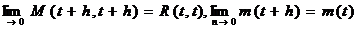
и, следовательно,

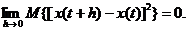
Необходимость условий теоремы доказана.

Для доказательства достаточности заметим, что из свойства 3 корреляционной функции следует, что

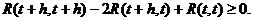
таким образом, правая часть выражения (4.14) есть сума неотрицательных величин. Если левая часть равенства сходится к нулю, то каждый член правой части также сходится к нулю и, таким образом, непрерывность процесса в среднеквадратическом означает непрерывность 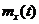. Для доказательства достаточности, заключающейся в непрерывности корреляционной функции, рассмотрим

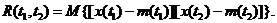
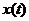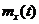Так как и - непрерывные функции

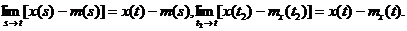
Используя равенство 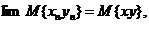убеждаемся, что

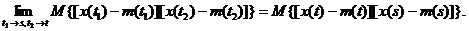
Определим теперь дифференцируемость случайной функции.

Определение 4.3.

Случайный процесс 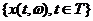второго порядка дифференцируем в среднеквадратическом в точке 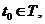если существует предел

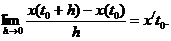
если процесс 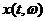дифференцируем для всех 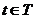и почти для всех 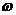, то говорят, что это дифференцируемый случайный процесс.

Следующая теорема часто используется при определении дифференцируемости случайного процесса.

Теорема 4.2. Случайный процесс 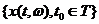второго порядка дифференцируем в среднеквадратическом в 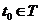тогда и только тогда, когда 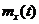дифференцируема в точке 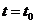и в точке 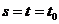существует вторая смешанная производная от корреляционной функции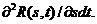

Для доказательства необходимости рассмотрим предел выражения

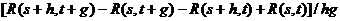
при .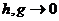

Сформируем последовательность Коши: (4.16)

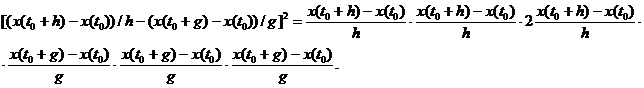
Взяв математическое ожидание от обеих частей равенства, получим:

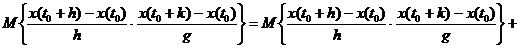
Если 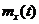- дифференцируемая функция и 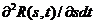существует, то

.

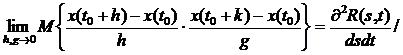
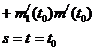Вычислив все три члена выражения (4.16),найдем что

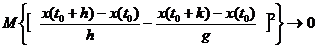
при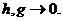

Положим теперь, что 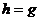и отметим, что правая часть выражения (4.16) есть сумма двух неотрицательных членов. Если левая часть сходится к нулю, каждый член правой части также будет сходиться к нулю.

Доказательство закончено. Непосредственно из теоремы следуют два следствия, которые могут быть полезными при анализе случайных процессов.

Следствие 1. Если случайный процесс 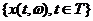дифференцируем, то

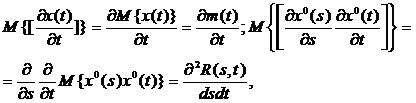где 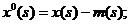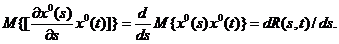(4.17)

Следствие 2. Если случайный процесс стационарен в широком смысле, то

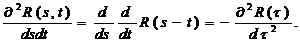(4.18)

Следовательно, для того чтобы стационарная случайная функция была дифференцируема, достаточно существования второй частной производной 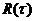при нулевом значении ее аргумента.