Дискретные случайные процессы

Примеры дискретных случайных процессов

Исключительно важную роль в задачах анализа и синтеза автоматизированных систем управления играют дискретные случайные процессы.

Дело в том, что в большинстве случаев процесс функционирования АСУ и ее элементов удобно представлять как последовательность выполнения некоторого набора действий (операций по подготовке данных и вводу, выполнение программ, передача данных и т.д.). Эти процессы рассматриваются во времени и одной из основных задач анализа и синтеза АСУ является исследование их временных характеристик, таких, как интервалы времени простоя устройств, времени выполнения программ, изменение производительности вычислительных систем и т. п. Для реальных АСУ типично наличие элементов случайности при инициировании запросов пользователей, в состоянии компонентов комплекс технических средств АСУ, в длительности выполнения программ, связанных с поиском и сортировкой, и т. д. Все эти обстоятельства вынуждают рассматривать процесс функционирования комплекса технических средств АСУ как случайный.

Пример 1. Простейшей моделью вычислительной системы пакетной обработки является модель [ 4 ].

Прочитанные перфокарты с заданиями через буфер ввода оперативной памяти записываются на магнитный диск, где ожидают очереди на выполнение. Выполнение задания (точнее – результаты выполнения заданий) выводятся на магнитный диск и затем через буфер вывода – на печатающее устройство.

В данной системе возможно возникновение очередей: в устройстве ввода с перфокарт, входных заданий на магнитном диске, выходных заданий на магнитном диске.

Предположим, что число заданий, поступающих в течение n – го периода, является случайной величиной, функция распределения которой не зависит от номера периода и имеет вид

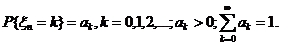(2.1.)

Предположим, что случайные величины 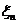независимы. Состояние системы в n – й момент времени определяется как число заданий, ждущих обслуживания к началу n – го периода. Если система находится в состоянии ???, то по прошествии одного периода она перейдет в состояние

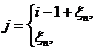если:

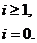
при условии, что за период будет выполнено ровно одно задание.

Очевидно, что если в среднем число заданий, поступающих во вводную очередь на МД, будет превышать число заданий, выводимых из ОП, очередь будет неограниченно возрастать. Очевидно также, что состояние вычислительной системы характеризуются числом 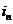и вероятностью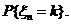

Пример 2. Этот пример связан с задачами управления запасами и снабжением, решаемых в АСУП.

Рассмотрим систему, в которую поступает некоторый товар или некоторое сырье, с целью постоянного удовлетворения спроса. Предположим, что пополнение запаса осуществляется в моменты времени t₁, t₂, ….., а суммарный спрос 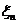на товар в интервале времени 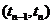представляет собой случайную величину с распределением

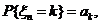к=0, 1, 2, …,

одинаковым для всех интервалов, причем 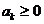и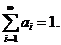

Уровень запаса фиксируется в начале каждого периода. Стратегия пополнения запаса такова: если имеющееся количество товара не превышает некоторого критического уровня s*, то производится немедленное пополнение запаса до уровня s > s*. Если же имеющееся количество товара больше s*, то пополнение не производится. Пусть x _n обозначает уровень запаса непосредственно перед моментом t _n. Пространство состояний процесса {x _n } складывается из возможных значений уровня запаса { x _n , x _n+1, x _n+2, …}.

Согласно описанному правилу уровня запаса двух последовательных периодов связаны соотношениями:

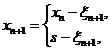если: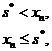

где 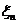– суммарный спрос за n – й период. Если предположить, что случайные величины 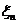независимы, то уровни запаса 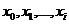образуют марковский процесс с дискретными состояниями.

Цепи Маркова

В примере 2 мы встретились с марковским процессом, пространство состояний которого является дискретным. Рассмотрим такие процессы подробнее.

Определение 2.1.

Марковский случайный процесс 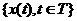называется марковской цепью {x _n}, если множество значений X является конечным или счетным, а аргумент T принимает значения { 0 , ±1_, ±2, …, ± n }.

Пространство состояний процесса удобно отождествлять с множеством неотрицательных целых чисел ( 0, 1, 2, …) и считать, что 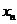находится в состоянии i , если .

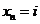Вероятность случайной величины x _n+1 оказаться в состоянии j , если известно, что 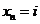обозначается формулой

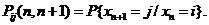
Эта вероятность называется переходной вероятностью за один шаг.

Если переходные вероятности 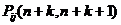не зависят от k = 0, ±1, ±2 … , то говорят, что марковский процесс обладает стационарными переходными вероятностями.

Пользуясь дискретностью множества Х и независимостью 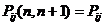от времени, можно записать в виде квадратной матрицы вероятности переходов

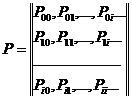
Определение 2.2

Матрица Р называется матрицей переходных вероятностей марковской цепи. Каждая строка этой матрицы представляет собой условное распределение случайной величины x _n+1 при условии, что 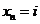, !!= 0, 1, 2,…. .

Очевидно, что элементы и строки матрицы обладают свойствами

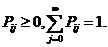
Обычно в вероятностных задачах анализа АСУ множество значений Х конечно и тогда матрица Р – конечная квадратная матрица.

Для стационарной марковской цепи выборочная траектория {x _n } представляет собой последовательность номеров ( или каких либо символов ), соответствующих состояниям, в которых процесс находится в моменты времени n = 1, 2, .….

Как правило, марковскую цепь рассматривают, начиная с некоторого момента времени t, причем полагая : t = 0. Обозначим 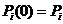- безусловную вероятность того, что в момент времени n = 0 процесс находится в состоянии 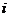. Тогда

Для стационарных марковских процессов справедлива следующая теорема.

Теорема 2.1. Для стационарной марковской цепи вероятность

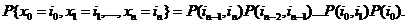(2.2) Для доказательства заметим, что по определению условной вероятности имеем

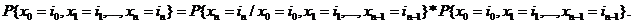
(2.3)

Но по определению марковского процесса

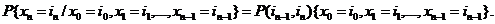(2.4)

Подставляя (2.3) в (2.4), получим :

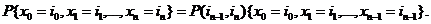
Продолжая по индукции, получим равенство (2.2).

2.2.2. Матрица вероятностей перехода за n шагов.

Одной из важнейших характеристик марковской цепи является матрица переходных вероятностей за n шагов 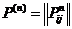, каждый элемент которой обозначает вероятность того, что процесс перейдет из состояния 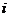в состояние за n шагов.

Независимость поведения от предыстории позволяет выразить вероятность 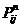через 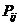, как это видно из следующей теоремы.

Теорема 2.2. Если 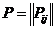- матрица одношаговых переходных вероятностей марковской цепи, то

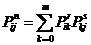(2.5)

Для любой фиксированной пары неотрицательных чисел

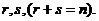
Для доказательства рассмотрим событие, состоящее в переходе из состояния 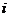в состояние за два шага ( n = 2 ). Это событие может произойти любым из следующих взаимно исключающих друг друга путей: на первом шаге – переход в некоторое промежуточное состояние k (k= 0, 1, 2 ….), затем на втором шаге, переход из состояния k в состояние . Так как процесс марковский, то вероятность второго перехода равна 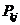, а первого 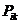. Отсюда в силу формулы полной вероятности получим

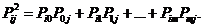
Для случая n > 2, повторяя рассуждения, приходим к такому же выводу. Формуле ( 2.5 ) можно придать рекуррентный вид.

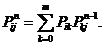
Другой удобной формой для представления 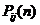является формула

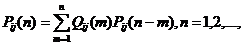(2.6)

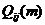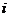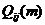где - вероятность перехода из в точно за m шагов ( т.е. без попадания в до m – го шага). Величина равняется, очевидно,

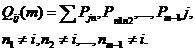(2.7)

Обозначим 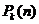- вероятность (полную) оказаться в момент времени n в состоянии с номером K. Тогда, как это видно из (2.5),

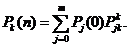(2.8)

Важнейшей задачей анализа марковских цепей является исследование асимптотического поведения вероятностей 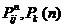при n → .

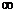Для проведения такого исследования введем классификацию состояний марковских цепей.

2.3. Классификация состояний марковских цепей

Введем следующие определения.

Определение 2.3.

Состояние s_n достижимо из состояния 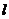, если существует такое n ≥ 0, что

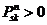, т.е. если вероятность попасть из состояния в состояние K – неотрицательное.

Определение 2.4.

Множество состояний С называется замкнутым, если любое состояние вне С не может быть достигнуто из С.

Определение 2.5.

Цепь называется неприводимой, если в ней нет никаких замкнутых множеств, кроме множества всех состояний, или, иными словами: цепь является неприводимой тогда и только тогда, когда любое ее состояние может быть достигнуто из любого другого состояния.

Рассмотрим теперь произвольное, но фиксированное состояние и предположим, что в момент О система находится в . Всякий раз, когда система возвращается в состояние , восстанавливается первоначальное положение. Время возвращения 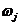является, очевидно, случайной величиной. Каждое состояние характеризуется своим распределением времени первого возвращения { }.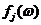

Величины 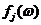можно вычислить, зная 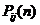и используя следующие соотношения:

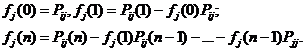(2.9)

Сумма 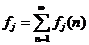представляет собой вероятность того, что, исходя из , система когда-нибудь вернется в .

Определение 2.6.

Состояние называется возвратимым, если 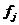= 1. Среднее время возвращения равно

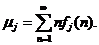
Состояние называется нулевым состоянием, если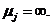

Если в начальный момент система находится в состоянии 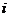, то время ожидания первого достижения имеет распределение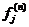

где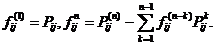

Состояние 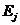невозвратимо, если 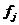<1. В случае если 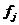= 1, но среднее время возвращения 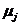бесконечно, состояние называется возвратным нулевым состоянием.

Определение 2.7.

Состояние называется периодическим с периодом t > 1, если 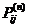= 0 для любого n некратного t и t - наименьшее целое число, обладающее этим свойством.

Определение 2.8.

Возвратное состояние, не являющееся ни нулевым, ни периодическим, будет называться эргодическим.

Для марковских цепей справедлива следующая теорема, касающаяся ее состояний, которую мы приведем без доказательства.

В неприводимой цепи Маркова все состояния принадлежат к одному и тому же типу: или они все невозвратные, или все возвратные нулевые, или все возвратные ненулевые.

Конечная цепь Маркова не содержит нулевых состояний и не может состоять только из невозвратных состояний [ 5 ].