В.49.Односторонние пределы: Асимптоты графика функции.

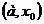
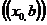Левой (правой) полуокрестностью точки называется произвольный интервал , где 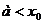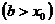слева (справа).

Число А называется пределом функции в точке 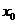слева (справа), если функция определена в некоторой левой (правой) полуокрестности точки 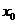и если для любого 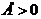существует 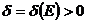такое, что для всех 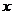, удовлетворяющих условию 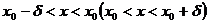, выполняется неравенство

.

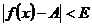В этом случае пишут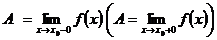

Пределы слева и справа называются односторонними пределами. Если 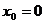, то односторонние пределы обозначают , .

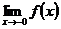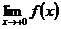Функция имеет предел в точке тогда и только тогда, когда в этой точке существуют оба односторонние предела, равные между собой.

В этом случае их общее значение и является пределом функции в точке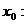

.

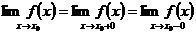Асимптота графика функции 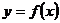- это прямая линия, к которой неограниченно приближается график данной функции, когда его точка неограниченно удаляется от начала координат.

Различают горизонтальную, вертикальную и наклонную асимптоты.

Прямая 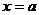называется вертикальной асимптотой, графика функции 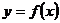, ес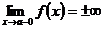ли

или .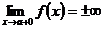

В случае вертикальной асимптоты 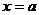функция является бесконечно большой в точке .

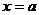Прямая 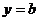называется горизонтальной асимптотой графика функции 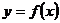, если .

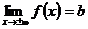Вертикальные асимптоты могут существовать у функций, которые определены не на всей числовой прямой.

Если областью определения функции является вся числовая прямая, то у функции нет вертикальных асимптот.

Прямая 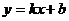называется наклонной асимптотой графика функци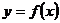и , при 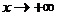, если

.

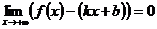Для нахождения коэффициентов 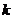и b применяют следующие формулы:

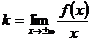(25)

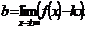(26)

Если хотя бы один из этих пределов равен 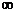или не существует, то у функции наклонных асимптот нет.

Если 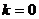, , 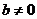то прямая 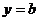является горизонтальной асимптотой. Горизонтальная асимптота – это частный случай наклонной асимптоты.

Заметим, что наклонных асимптоты у функции может быть не больше двух, а вертикальных может быть сколько угодно.

В33.. Непрерывность функции. Классификация

Точек разрыва.

Функция называется непрерывной в точке , если она определена в этой точке в некоторой ее окрестности и

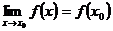(27)

Если функция 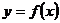непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.

Существуют и другие определения непрерывности функции в точке. Функция называется непрерывной в точке , если она определена в этой точке и в некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:

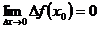(28)

Непрерывность функции в точке определяется также на основе односторонних предметов.

Функция называется непрерывной в точке , если она определена в этой точке и некоторой ее окрестности и существует односторонние пределы (конечные) такие, что

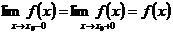(29)