Используя теорему о пределе частного двух функций, получаем равенство (1).
Применение производных к исследованию функций.
Функция 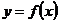 называется возрастающей в промежутке
называется возрастающей в промежутке 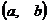 , если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует и большее значение функции.
, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует и большее значение функции.
Таким образом, если 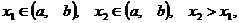 то
то
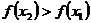 (5.1)
(5.1)
Аналогично функция 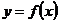 называется убывающей в промежутке
называется убывающей в промежутке 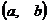 , если для двух любых значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции.
, если для двух любых значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции.
Если 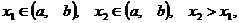 то
то
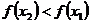 (5.2).
(5.2).
Аналогичное определение дается возрастанию или убыванию функции на отрезке 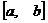 .
.
Из этих определений вытекает, что для возрастающей функции приращение функции и приращение аргумента имеют один и тот же знак, в силу чего их отношение положительно: 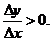 (5.1*)
(5.1*)
Для убывающей функции эти приращения имеют противоположные знаки, в силу чего 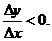 (5.2*)
(5.2*)
Если функция 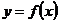 на данном отрезке (или в данном промежутке) переходит от возрастания к убыванию или наоборот (один или несколько раз), то ее называют колеблющейся на данном отрезке (в данном промежутке).
на данном отрезке (или в данном промежутке) переходит от возрастания к убыванию или наоборот (один или несколько раз), то ее называют колеблющейся на данном отрезке (в данном промежутке).
Те значения аргумента, при которых функция достигает своих наибольших или наименьших, по сравнению с соседними, значений, называются точками максимума и минимума.
Определение. Точка 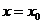 называется точкой максимума функции
называется точкой максимума функции 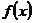 , а значение
, а значение 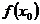 называется максимумом этой функции, если существует некоторая окрестность точки
называется максимумом этой функции, если существует некоторая окрестность точки 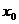 [т. е. промежуток
[т. е. промежуток 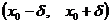 ], такая, что значение функции в любой точке этой окрестности будет меньше, чем ее значение в самой точке
], такая, что значение функции в любой точке этой окрестности будет меньше, чем ее значение в самой точке 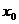 , т. е. меньше, чем максимум
, т. е. меньше, чем максимум 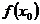 :
: 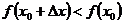 при
при 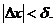 (5.3)
(5.3)
Аналогично (с заменой слова «меньше» на «больше») определяются точка минимума и минимум функции. Если 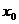 — точка минимума, a
— точка минимума, a 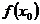 минимум, то имеют место следующие неравенства:
минимум, то имеют место следующие неравенства: 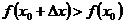 при
при 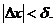 (5.4)
(5.4)
Точки минимума и максимума объединяются под общим названием точек экстремума, а минимум и максимум функции объединяются общим названием экстремум функции.
Экстремумы функции 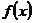 , определенные выше с помощью неравенств (5.3) и (5.4), часто называются строгими экстремумами, в отличие от нестрогих, где предполагаются неравенства вида
, определенные выше с помощью неравенств (5.3) и (5.4), часто называются строгими экстремумами, в отличие от нестрогих, где предполагаются неравенства вида 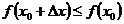 и соответственно
и соответственно 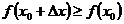 .
.
Исследование функции на возрастание – убывание..
Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка X, то она возрастает на этом промежутке.
Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка X, то она убывает на этом промежутке.
Для отыскания наибольшего и наименьшего значений на отрезке пользуются следующей схемой:
1. Находят производную 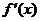 .
.
2. Находят критические точки функции, в которых 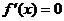 или не существует.
или не существует.
3. Находят значения функции в критических точках и на концах отрезка и выбирают из них наибольшее fнаиб и наименьшее fнаим.
