Раскрытие неопределенностей.

Раскрытием неопределенности в математическом анализе называют отыскание предела 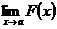, когда функция 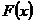непрерывна вблизи точки 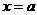, но не определена в самой этой точке, а непосредственная подстановка в формулу записи этой функции значения 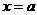приводит к выражению неопре­деленного вида:

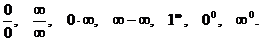
[Подобная же задача возникает и при отыскании .]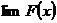

Теперь, опираясь на теорему Коши, выведем правило Бернулли — Ло­питаля для раскрытия неопределенностей, использующее производные.

Основными видами неопределенностей являются два: 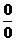и .

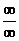Раскрытие этих неопределенностей означает вычисление предела отно­шения двух бесконечно малых и предела отношения двух бесконечно боль­ших. Для этих двух видов неопределенностей и будет выведено сейчас пра­вило Бернулли — Лопиталя. Вывод правила разбивается на 4 случая. Первые два посвящены отношению двух бесконечно малых 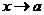(при и при 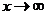); вторые два - отношению двух бесконечно больших 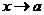(при и при ).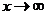

Остальные виды неопределенностей, как увидим дальше, приводятся к основным двум видам: 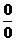и .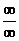

I случай. Неопределенность вида 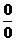(при 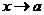). Пусть требуется найти 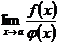, когда 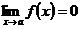и .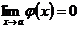

Примем 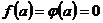; тогда функци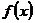и и 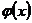будут непрерыв­ными в точке .

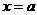Предположим, что обе функци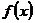и и 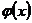дифференцируемы вблизи точки 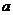, причем 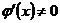. Докажем при этих условиях, что если су­ществует конечный или бесконечный предел отношения производных

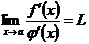, то 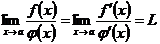, т. е. что искомый предел отношения функций в этом случае также существует и равен пределу отношения производных.

Для доказательства применим к функциям 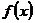и 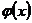на некотором отрезке 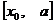теорему Коши, выбрав за 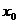произвольное значение , принадлежащее той окрестности точки 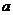, в которой обе функции будут непрерывны и, кроме того, дифференцируемы вблизи точки 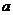, т. е. во всех точках этой окрестности, кроме, может быть, самой точки 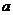. По­лучаем

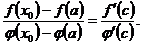
Это равенство, в силу того что 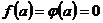, приводится к виду

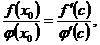где 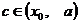; если теперь устремить 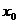к 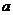, то одновременно и 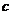будет стре­миться к 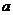; поэтому

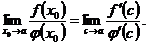
В этом предельном равенстве ничто не изменится, есл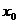и и 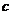заменить прос­то символом :

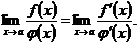(5.12)

В самом деле, 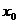есть произвольное, достаточно близкое к 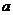значе­ние аргумента . Поэтому можно символ 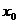заменить просто символом в левой части предельного равенства. Далее, по условию существует

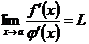при произвольном способе стремления к 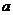; значит, существует и равен ему 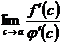. Поэтому можно в правой части предельного равенства заменять 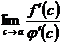на .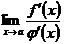

Тот же результат получим, если вместо отрезка 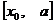, рассмотрим отрезок 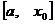. Равенство (14.12) и дает нам правило Бернулли — Лопиталя для рассматриваемого нами случая.

II случай. Неопределенность вида 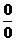(при 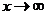). Докажем, что прави­ло (5.12) остается в силе и в случае, когда .

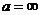Пусть требуется найти 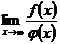, если .

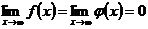Предположим, что при всех достаточно больших по абсолютной ве­личине значениях (т. е. при 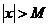, 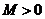) обе функции дифферен­цируемы и 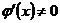и что существует (конечный или бесконечный) 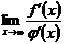. Докажем, что тогда .

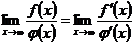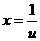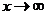Для доказательства перейдем к новому аргументу, положив ; при , и .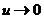

Легко видеть, что к отношению 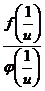правило (5.12) применимо: в окрестности точки 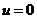обе функции дифференцируемы, производная 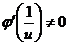и существует .

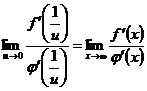Но тогда, применяя правило (5.12), получим .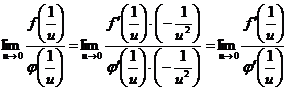

Возвращаясь к аргументу , находим то, что было необходимо. Это же правило сохраняется и в том случае, когда аргумент стремится к бесконечности только по положительным или только по отрицательным значениям, т. е. когда 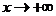или .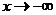

III случай. Неопределенность вида 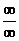(при 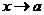). Пусть теперь требуется найти 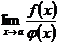, если .

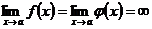Пусть и в этом случае будут соблюдены условия, оговоренные нами при рассмотрении I случая, т. е. пусть вблизи точки 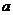обе функци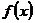и и 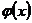дифференцируемы и 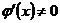. Докажем тогда, что если существует (конечный или бесконечный) 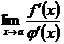, то правило Бернулли— Лопиталя (512) остается в силе, т. е. .

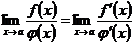Для доказательства возьмем в окрестности точки 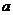два значения : 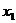и 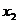, причем пусть 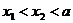, если точк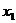и и 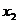берутся слева от 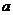, и 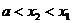, если берутся справа от 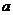. Тогда на отрезке 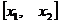(или 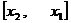к отношению функци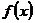й и 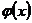применима теорема Коши:

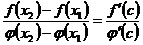, (5.14) где 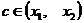(или ).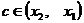

Разберем сначала случай, когда существует конечный предел отношения производных:

.

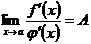Задав произвольно малое положительное число 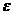, определим 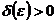так, чтобы при 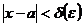выполнялось неравенство

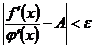. (5.15)

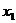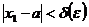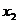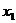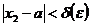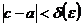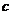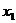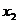Выберем теперь так, чтобы и фиксируем его зна­чение; тогда, согласно условию выбора , для всякого выбранного будем иметь и подавно и , поскольку за­ключено между и . Поэтому в силу неравенства (5.15) будем иметь

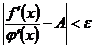, или .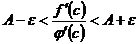

Заменяя в этом неравенстве, согласно (14.14), отношение 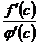рав­ным ему отношением

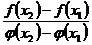, находим 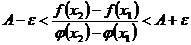. (5.16)

Преобразуем это неравенство следующим образом: 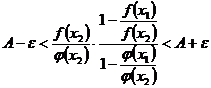.(5.17)

Если теперь устремить 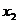к 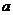, не изменяя 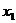, то в силу условий 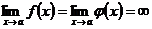будем иметь

.

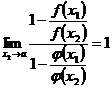Поэтому при заданном 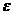найдется таксе 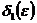, что при 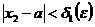, будет выполняться неравенство:

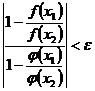, или .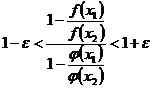

Перемножая теперь почленно неравенства (517) и (5.18), что воз­можно, поскольку члены неравенства (5.18) положительны, получаем 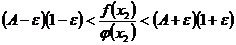.(5.19)

Но 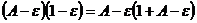, ; следовательно, неравенство (5.19) показывает, что при выбранных значениях 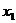и 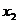разность между переменной величиной 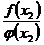и постоянной 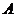будет величиной бесконечно малой.

Поэтому 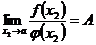и, следовательно, 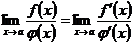. (5.20)

Если же 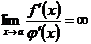, то, во-первых, тогда 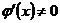в достаточно малой окрестности точки 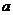(иначе, отношение 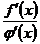было бы беско­нечно большим), во-вторых, 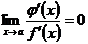(поскольку величина, обратная к бесконечно большой, бесконечно мала), а потому к обратному от­ношению 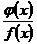применимо предыдущее правило, следовательно,

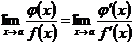, откуда следует справедливость и формулы (5.20).

IV Случай. Неопределенность вида 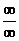(при 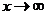). Правило (5.20) сохраняется и при :

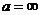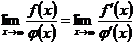(5.21) при условии, что 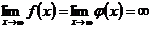и что обе функци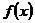и и 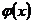дифференцируемы при всех достаточно больших по абсолютной величине значениях ( 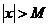, 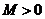), причем 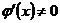, и при условии, что существует (конечный или бесконечный) .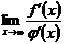