Перемена местами двух уравнений.

Пусть теперь .(Если ,то мы поменяем местами первое уравнение с тем уравнением, где коэффициент при 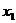отличен от нуля). Исключим теперь 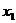из всех уравнений системы, начиная со второго. Для этого ко второму уравнению прибавим первое уравнение, умноженное на ( ), затем прибавим к третьему уравнению первое, умноженное на ( ) и т.д. к последнему уравнению прибавим первое, умноженное на ( ). При этом получим систему

(3.9)

Далее, применив те же рассуждения к системе (3.9) исключим из уравнений, начиная с третьего 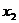и т.д.

Продолжая этот процесс, мы придем к одному из двух случаев:

1. Либо после определенного шага получиться система, содержащая уравнение вида и . Тогда наша система не имеет решений, т.е. несовместна.

2. Либо система не содержит уравнение вида и . Тогда рано или поздно мы придем к системе

(3.10)

Возможны два случая:

a) . Тогда последнее уравнение системы (3.10) имеет вид: , откуда . Из предпоследнего уравнения находим и т.д. из первого уравнения системы (3.10) находим .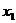

b) . Тогда система имеет бесчисленное множество решений.

Замечание. С практической точки зрения процесс решения системы (3.8) можно облегчить, если вместо преобразований над самой системой производить преобразования над соответствующей расширенной матрицей системы:

III. Метод обратной матрицы (матричный способ).

Пусть задана система 3хуравнений с тремя неизвестными

(3.12)

Рассмотрим три матрицы:

, ,

Тогда, пользуясь правилом умножения матриц, систему (3.12) можно записать в матичной форме:

(3.13)

Действительно, умножив матрицы левой части, получаем:

(3.14)

Из определения равенства двух матриц следует, что (3.12) и (3.14) равносильны. Коротко (3.13) записывают

(3.15)

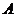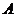Пусть определитель матрицы отличен от нуля, т.е. . Тогда для матрицы существует обратная матрица . Умножим левую и правую части равенства (3.15) слева на матрицу . Имеем:

(3.16)

Так как и , то из (3.16) получаем

(3.17)

Таким образом, чтобы решить систему линейных уравнений (3.12) матричным методом необходимо: 1) Вычислить определитель системы и убедиться, что (В случае, если , то матрица 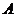не имеет обратной матрицы и применить матричный метод нельзя); 2) Найти обратную матрицу ; 3) применить формулу .

Комплексные числа в алгебраической, тригонометрической и показательной формах, действия над ними.

Понятие комплексного числа. Основные определения.

Числа вида , где а и b действительные числа, а - мнимая единица, называются комплексными. Число «а» - называется действительной частью комплексного числа и обозначается так: , число «b» называется мнимой частью и обозначается так: .

Например, .

Комплексные числа называются сопряженными.

Два комплексных числа равны между собой тогда и только тогда, когда у них соответственно равны действительные и мнимые части .

Относительно комплексных чисел не принято никакого соглашения, какое из них считать больше другого.

Действия над комплексными числами в алгебраической форме. Сложение, вычитание и умножение комплексных чисел.