Проверка статистических гипотез. Критерии согласия Пирсона и Колмогорова.

Статистическая гипотеза-утверждение относительно распределения с.в. ген. совокупности. Гипотеза, подверг. Проверке, называется нулевой. (Н₀). Если Н₀ отвергается, то принимается альтернативная гипотеза Н₁.Правило, согласно которому проверяется Н₀, называется статистической проверкой гипотезы Н_0. Правило, по кот. принимается решение о принятии или отклонении гипотезы, называется критерием (К).

Т.к.решение принимается на основе выборки наблюдений с.в. Х, то необходимо выбрать подх. статистику (оценку), наз-ую статистикой z критерия К.

Критерий, основанный на исп-ии заранее заданного ур-ня значимости, наз-ся критерием значимости. Множество всех значений z стат., при кот. принимаются решения, отклон. гипотезу Н₀, наз-ся критической областью. Совокупность значений статистики z, при кот. Н₀ принимают, наз-ют областью принятия гипотезы. Точки, отд.критическую область от области принятия решений, называют критическими.

Схема статистической проверки гипотезы:1) формулировка Н₀ и Н₁ гипотез;2) выбор соответствующего уровня значимости;3) определение объёма выборки;4)выбор статистики z критерия для проверки гипотезы Н_0;5)определение критической области и области принятия гипотезы;6)формулировка правила проверки гипотезы;7) применение статистического решения

Критерий согласия Пирсона.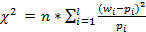

w_i – относительные частоты, заданные статистической таблицей; p_i – вероятности, получ. По некоторому теорет. З-ну распределения

Далее рассматривается разность. r=l-t, l-число разрядов стат. Таблицы;t-число условий, налагаемых на частоты;r-число степеней свободы

Например для норм. З-на распред., t=3. 1)w_i=1;2) 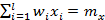- в теорет. З-не распред.;3)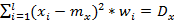

Используя табл.приложений по значениям 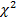и r определяют вероятность р, кот.хар-ет вероятность согласованности теории и статистических распределений. Если р<0,1, то делают вывод, что теория плохо воспроизводит эксперимент. Если р>0,1, то гипотеза о принятии теор.распределения не противоречит опытным данным.

Критерий согласия Колмогорова.

Пусть дано статистическое распределение х₁, х₂, …, х_l, где х_l-ср.значение соотв.интервалов с.в.

х	Х1	Х2	…	хl
w	W1	W2	…	wl

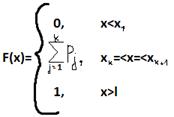В кач-вем меры расхождения между теор. и статист. распределением, в критерии Колмогорова рассм-ся макс.значения модуля разности между статистической ф-ии распред.(F^*(x)) и теор. (F(x)).

P_j=h*f(x_j) , j=1,…l

f(x)- плотность распределения с.в. Х

Сначала находим величину Х=D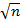

D=max|F^*(x)-F(x)|

n-объём выборки

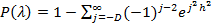
Эта формула определяет вероятность того, что за счёт сл.прич., макс.расхождение между F^*(x) и F(x) окажется не меньше, чем фактически наблюдаемая. Если вероятность Р(λ) мала (Р^*<0,05), то гипотезу следует отвергнуть как неправдоподобную, а при сравнительно больших значениях Р(λ) гипотезу можно считать совместимой с опытными данными.

Р(λ) находят из таблиц.