Линейные неоднородные ДУ 2-ого порядка. Теорема о структуре общего решения неоднородного ДУ.

Линейное неод-ое Д.У. 2-го пор-ка имеет вид: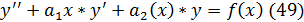

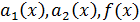– заданные ф-ии.

Теорема.Общее реш-ие лин-ого неоднород-го Д.У. есть сумма его частного реш-ия и общего реш-ия соот-его однород-го ур-ия. Из теоремы следует что отыскание общего реш-ия неод-ого ур-ия нужно найти общ. реш-ие соотв-его однород. ур-ия и какое-либо част-ое реш-ие.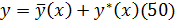

Ф-ию 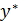можно определить методом вариации произвольных постоянных или методом Лагранжа.

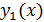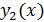Пусть и – фундаментальная сис-ма реш-ий однород-го ур-ия.

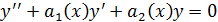А общее реш-ие это ур-ие 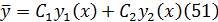- общее реш-ие однород. Д.У.

Част. реш-ие 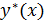неод-го Д.У. (49) будем искать в виде (51), считая пр этом 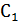и 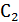не постоянными, а независимыми ф-иями переменной x.

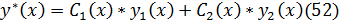
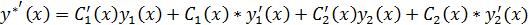
Т.к. надо определить 2 ф-и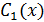и и 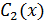, то одно соотношение между ними можно выбрать произвольно. Пусть 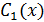и 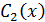такие, что справедливо рав-во: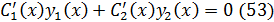

;

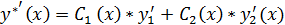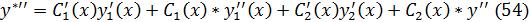
Подставляя выр-ие 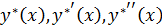в ур-ие (49):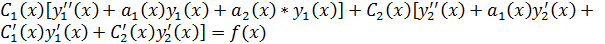

Т.к. 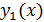и 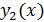– реш-ия однород-го ур-ия, то выр-ия в кв. скобках равны 0. И следовательно: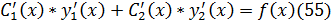

Объеденив последние рав-ва с рв-вом (53) получим:

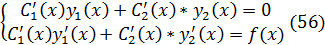
В этой сис-ме неизвестным яв-ся: 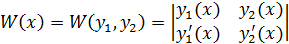линейно незав-ых фун-ий следовательно W(x)≠0

Решив сис-му (56) получим: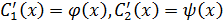

Проинтегрировав рав-во найдем :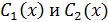

Подставив их в выр-ие (52), получим частное реш-ие неоднородного ур-ия (49).

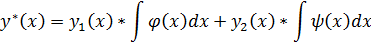
15.Метод вариации произвольных постоянных (Лагранжа) для отыскания частного решения линейного неоднородного ДУ 2-ого порядка.

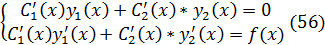
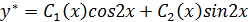
Сис-ма (56) будет иметь вид:

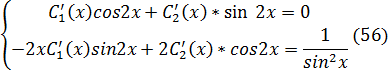
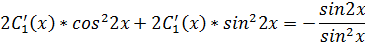
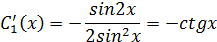
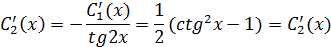
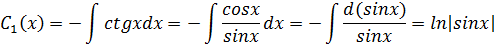
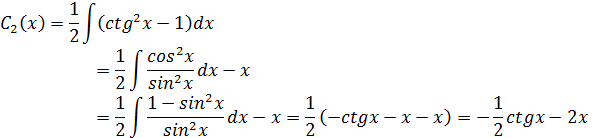
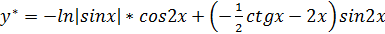– част. реш-ие

Линейные неоднородные ДУ с постоянными коэффициентами и специальной правой частью.

Рассмотрим ур-ие 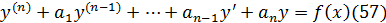, где a1,a2,…,an – заданные ф-ии от x или постоянные числа.

Предположим, что известно общ. реш-ие 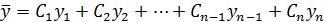соответств-его однород. ур-ия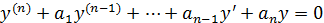

Для специального вида ур-ия (57) частное реш-ие можно найти с пом-ю метода неопр-ых коэф-ов (без применения операции интегрирования). Этот метод исп-ся если правая часть ур-ия (56) имеет вид:

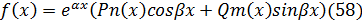Это многочлены с действительными коэффициентами степеней m и n соответственно. α и β – действ-ые числа. Частные случаи выраж-ия (58) и (59) сведем в таблицу.

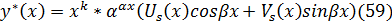
Правая часть f(x) Д.У.	Корни характерист-ого ур-ия	Вид частного реш-ия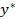
1) f(x)=Pn(x)	Если λ=0 то –не явл-ся корнем хар. ур-ия   Если λ=0 – яв-ся корнем хар. ур.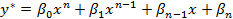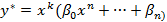
2)	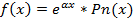Λ=α – не яв-ся корнем хар. ур-ия   Λ=λ – яв-ся корнем хар. ур-ия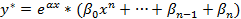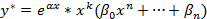
3)	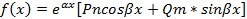Λ=α+iβ – не яв-ся корнем хар. ур-ия   Λ=α+iβ - яв-ся корнем хар. ур-ия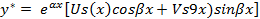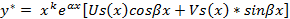

Системы ДУ. Нормальные системы. Теорема о существовании и единственности решения нормальной системы ДУ. Задача Коши для системы ДУ.

Существуют процессы, которые невозможно описать одним ДУ. Например, если материальная точка, массой m, движется под действием переменной силы F(t,r,r`) по закону r = r(t), то векторная функция r (t) = (x(t), y(t), z(t)) удовлетворяет уравнению:

m 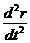= F (t,r, ) – векторное уравнение эквивалентно системе скалярной функции

m 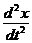= F₁ ( t,x,y,z,x`,y`,z`); m 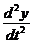= F<sub>2</sub> (t,x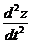,y,z,x`,y`,z`); m = F₃ (t,x,y,z,x`,y`,z`)

где F₁, F₂, F₃ – проекции вектора F на оси координат.

Система n ДУ 1-го порядка

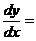f₁(x₁,y₁,y₂…..,y_n); 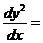f₂(x₁,y₁,y₂…..,y_n);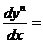_{……………;} f_n(x₁,y₁,y₂…..,y_n)

называется нормальная система.

Решением нормальной системы n ДУ на интервале (a;b) называется совокупность функций: y ₁ = y ₁ (x); y ₂ = y ₂(x);…………..;y _n = y _n (x) непрерыв. диф на (а,b), кот при подстановке в уравнения системы обращают их в тождества.