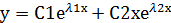Уравнение в полных дифференциалах.

Д.У вида Р(х,у)dх + Q(x,y)dy=0 называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции u(x,y)

Теорема.

Уравнение Р(х,у)dх + Q(x,y)dy=0 с непрерывной диф. функцией Р(х,у) и Q(x,y) является уравнением в полном дифференциале тогда и только тогда, когда выполняется условие: ðP/ðy=ðQ/ðx.
Доказательство.Необходимось:

пусть левая часть ур. Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал неявной ф-ииu(x,y)

Р(х,у)dх + Q(x,y)dy=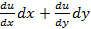

P(x,y)= 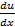Q(x,y)=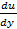

Продифференцируем 1-е соотношение P(x,y)= 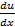по у, а 2-е Q(x,y)= 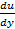по х.

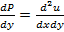и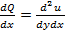

В силу равенства получаем: ðP/ðy=ðQ/ðx

Достаточность:

при выполнении усл. 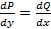и Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал некоторой ф-ииu(x,y).

Интегрируя по х из P(x,y)= 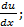Q(x,y)= 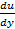: u(x,y)=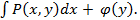

Подберем ф-ю 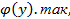чтобы выполнялось 2-е соотношение. Для этого продифференцируем равенство по у и результат приравняем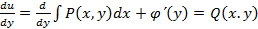

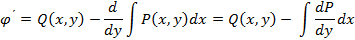
Необходимо показать что первая часть равенства не зависит от х.

Интегрируем рав-во и получаем:

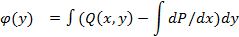
U(x,y)=C общее решение уравнения Р(х,у)dх + Q(x,y)dy=0

10.Дифференциальные уравнения высших порядков. Теорема о существовании и единственности решения. Задача Коши. Приемы понижения порядка (на примерах ДУ 2-ого порядка).

F(x,y, y´…… 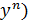=0 – наз. диф. ур. n-ого порядка. Будем предполагать, что оно разрешается относительно n-ой произ.

)

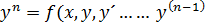Теорема Коши.

Если ф-я 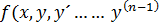и её частная производная от аргумента y,y´, 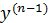определена и непрерывна в области R, содерж. точку( 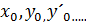)то в некоторой окрестности точки х0 существует ед. решение ур. 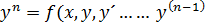)удавле. усл.y(x0)=y0; y´(x0)=y 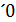; … 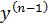(x0)= )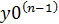

Это условие есть условие Коши.

Задача отыскания решения ур. 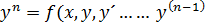)удовл. этим усл. наз. задачей Коши для ур. )

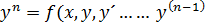В зад. Коши для диф. ур. 2-го порядка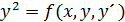

В некоторых частных случаях д.у. высших порядков можно решать методом понижения порядка.

1. у´´=f(x)т.к. у´´=(у´)´, то интегр. левую и правую часть

у´=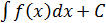

y=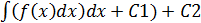

С1 и С2 – производные константы

2. у´´=f(x, y´) ,у´=z=z(x), y´´=z´, z´=f(x.y)

z= 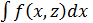z(x)=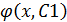

y´=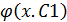

y= 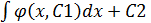-общее решение

3. y´´=f(y,y´) не содержащие явно независ. переменных х. Вводится новая ф-яz(y) и тогда у´=z ;y´´=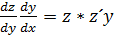

Подставив в исх. ур. полученное ур. z*z´y=f(y,z) в котором играет роль независ. перемен. у. Решив его, найдём z= 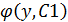Подставим 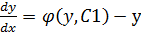равнение с разделяющимися переменными

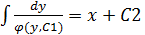- общее решение диф. ур.

Линейные однородные ДУ 2-ого порядка с постоянными коэффициентами. Характеристическое уравнение. Случай действительных различных и кратных корней характеристического уравнения.

Определение.

Ур.вида у´´+ру´+qy=0, p,q- наз. линейн. однород. диф. ур. с постоянными коэффициентами. Будем иск.решение ур. у´´+ру´+qy=0 в соот. с методом Эйлера у=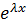

y´=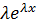

y´´=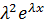

yи y´, y´´ подст. в ур. у´´+ру´+qy=0

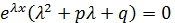
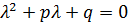–характеристическое ур.

1,Пусть корни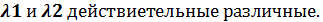

у1=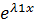

у2=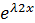

Т.к. определитель Вронского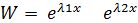

= =

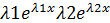
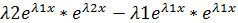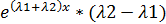
Решение -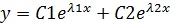

2)

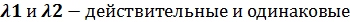
у1= 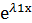– частное решение уравнения у´´+ру´+qy=0

Покажем, что в этом случае у2=х 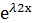также явл. решением ур. у´´+ру´+qy=0

Т.к. у2= 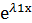+х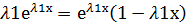

у2=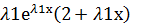

Общее решение ур.