Умножение матриц. Свойстваумножения.

Умножение матриц. Свойстваумножения.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы А_m×n на матрицу В_n×p, называется матрица С_m×p такая, что
с_ik = a_i1 × b_1k + a_i2 × b_2k + ... + a_in × b_nk,
т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера.

Свойства умножения матриц:Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка.
А × Е = Е × А = А

Умножение матриц обладает следующими свойствами:
1. А × (В × С) = (А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В) × С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0 = 0; 0 × А = 0;
6. (АВ)^Т = В^ТА^Т;
7. (АВС)^Т = С^ТВ^ТА^Т;
8. (А + В)^Т = А^Т + В^Т;

Понятие вектора. Линейные операции над векторами.

Вектором наз. упорядоченная совокупность чисел Х={X₁,X₂,...X_n} вектор дан в n-мерном пространстве. Т(X₁,X₂,X₃). n=1,2,3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.

Линейные операции над векторами обладают следующими свойствами:

1. а+b=b+а

2. (а +b) +с=а + (b +с),

3. λ1 • (λ2 •а) =λ1 •λ2 •а,

4. (λ1 +λ2) •а =λ1 •а +λ2 •а,

5. λ • (а +b) =λ •а+λ •b.

Базис и координаты вектора.

Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

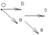Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.

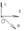Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

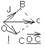ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе

Миноры, алгебраические дополнения. Теорем о разложении определителя по элементам ряда

Свойства Определителей

Св-ва: 1)Определитель не измениться, если его строки заменить столбцами и наоборот; 2) При перестановке 2-х парал рядов опред меняет знак на противоположный; 3)Определитель, имеющ два одинаковых ряда=0; 4)Общий множитель элементов какого-то ряда опред, можно вынести за знак опред; 5)если все элем ряда пропорц соотв элем парал ряда, то такой опред=0; 6)если все элем строки(столбца) определителя=0, то опред=0; 7) если элем определителя представ собой суммы двух слогаемых, то опред может быть разложен на сумму двух соотв определителей; 8)Определитель не изменится, если к элем одного ряда прибавить соотв элементы парал ряда, умноженного на число; 9)для разлож опред обычно выбирают тот ряд, где есть нулевые элементы, т.к. соотв им слаг будут=0; 10)сумма произведений элементов какого-либо ряда определителя на алг. дополнение параллельного ряда соотв элементов равно 0;

Общее уравнение плоскости.

Ax+By+Сz-Ax₀-By₀-Сz₀=0

-Ax₀-By₀-Сz₀=D, где D=Ax+By+Сz

Ax+By+Сz+D=0

Частный случай:

Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)

Если A=0, то By+Сz+D=0

Если B=0, то Ax +Сz+D=0

Если C=0, то Ax+By+D=0

Если A=B=0, то Сz+D=0

Если A=C=0, то By+D=0

Если A=D=0, то By+Сz=0

Если B=D=0, то Ay+Сz=0

Угол между плоскостями

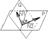
N₁,N₂-нормальные векторы плоскости.

P:A₁x+B₁y+C₁z+D₁=0

Q:A₂x+B₂y+C₂z+D₂=0

P^Q{A₁,B₁,C₁}

Q^N₂{A₂,B₂,C₂}

Угол между плоскостями

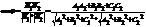
1)Пусть P^Q<=>N₁^N₂

A₁A₂+B₁B₂+C₁C₂=0 условие перпендикулярности P^Q.

2) Пусть P^Q<=> N₁^N₂

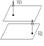
A₁/A₂=B₁/B₂=C₁/C₂- Условие параллельности 2х плоскостей.

A₁/A₂=B₁/B₂=C₁/C₂=D₁/D₂- Условие совпадения 2х плоскостей.

Парабола и ее свойства.

Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax², где х и у - текущие координаты, а- нек. число, наз. параболой.

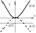Если вершина нах. в О(0,0), то ур-е примет вид

y²=2px-симметрично отн. оси ОХ

х²=2pу-симметрично отн. оси ОУ

Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.

Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2

Св-ва:

1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax².

5.1. Канонические и параметрические уравн прямой. Урав прямой, проходящ через две точки.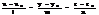

l m n

S{x₂-x₁,y₂-y₁,z₂-z₁}

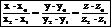
Каноническое уравнение прямой в пространстве:

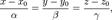
где 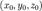— координаты некоторой фиксированной точки 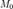, лежащей на прямой, 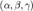- координаты вектора, коллинеарного этой прямой.

Параметрические уравнения прямой могут быть записаны в виде:

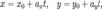
где t — производный параметр, при этом

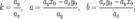
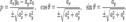
Гипербола и ее св-ва.

Кривая 2го порядка наз. гиперболой, если в ур-ии Ax²+Cy²=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0

б) Если d>0, то каноническое ур-е гиперболы примет вид: x²/a²-y²/b²=1, F1(c,o) и F₂(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.

Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.

б) если d=0, ур-е примет вид x²/a²-y²/b²=0, получаем 2 перекрестные прямые х/а±у/b=0

в) если d<0, то x²/a²-y²/b²=-1 - ур-е сопряженной гиперболы.

Определение

Если 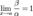, то бесконечно малые величины α и β называются эквивалентными ( ).
Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При справедливы следующие соотношения эквивалентности (как следствия из т. н. замечательных пределов):

;

;

;

.

Й, замечательный предел.

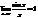Доказательство: докажем для 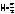справедливость неравенства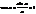

В силу четности входящих в неравенство ф-ий, докажем это неравенство на промежутке 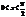Из рисунка видно, что площадь кругового сектора

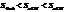
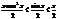, так как х>0, то ,

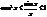2. следовательно, что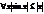

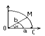
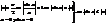
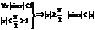
1. Покажем, что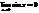

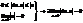
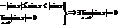
2. Докажем, что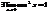

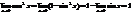
3. Последнее утверждение:

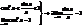
Второй замечательный предел

lim(n®¥)(1+1/n)^n=e Док-во:

x®+¥ n x:n=[x] => n£x<n+1 => 1/(n+1)<1/x<1/n

Посколько при ув-нии основания и степени у показательной ф-ции, ф-ция возрастает, то можно записать новое неравенство (1/(n+1))^n£(1+1/n)^x£ (1+1/n)^(n+1) (4)

Рассмотрим пос-ти стоящие справа и слева. Покажем что их предел число е. Заметим (х®+¥, n®¥)

lim(n®¥)(1+1/(n+1))=lim(n®¥)(1+1/(n+1))^n+1-1= lim(n®¥)(1+1/(n+1))^n+1*lim(n®¥)1/(1+1/(n+1))=e

lim(n®¥)(1+1/n)^n+1= lim(n®¥)(1+1/n)^n* lim(n®¥)(1+1/n)=e*1=e

10.3.Сравнение бесконечно малых. Эквивалентные бесконечно малые.

Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.Например, функция f(x) = x¹⁰ стремится к нулю быстрее, чем функция f(x) = x.Опр. Если 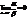, то функция a называется бесконечно малой более высокого порядка, чем функция b.

Опр. Если 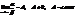, то a и b называются бесконечно малыми одного порядка.Опр. Если 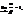то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.Пример. Сравним бесконечно малые при х®0 функции f(x) = x¹⁰ и f(x) = x. 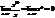т.е. функция f(x) = x¹⁰ – бесконечно малая более высокого порядка, чем f(x) = x. Опр. Бесконечно малая функция a называется бесконечно малой порядка kотносительно бесконечно малой функции b, если предел 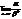конечен и отличен от нуля.Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 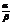не имеет предела, то функции несравнимы.

Свойства эквивалентных бесконечно малых.1) a ~ a, 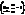2) Если a ~ b и b ~ g, то a ~ g, 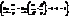3) Если a ~ b, то b ~ a,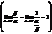

4) Если a ~ a₁ и b ~ b₁ и 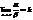, то 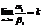и или .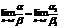

Следствие: а) если a ~ a₁ и 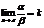, то и 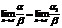б) если b ~ b₁ и 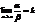, то 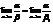Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.

12.3. Непрерывность функции в точке. Действия над непрерыв функциями

x=x₀+Dx, Dx=x-x₀

Dy=f(x₀+Dx)-f(x₀)

Ф-ция y=f(x) наз. непрерывной в точке x₀, если она определена в окрестности этой точки, а limDy=0. (бесконеч.малая. приращению аргумента соответствует б.м. приращению ф-ции).

limDy=lim[f(x)-f(x₀)]=limf(x)-limf(x₀)=0, то

limf(x)=limf(x₀)

x®x₀

Ф-ция непрерывна в точке х₀, если ее предел = значению этой ф-ции в точке х₀

Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.

Теорема Лагранжа.

Если функция f(x) непрерывна на [a,b] и дефференцирована на (a,b), то сущест.

т. с(a,b), такая, что: f(b)-f(a)=f’(c)(b-a).

Доказательство:применим т.Коши, взяв только g(x)=x, тогда g’(x)=1¹0.

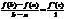
Теорема Коши.

Если f(x), g(x) удовл. трем условиям:

1). f(x), g(x) непрерыв. на промеж [a,b]

2). f(x), g(x) деффер. на интервале (a,b)

3). g’(x)¹0 на интер. (a,b), то сущ. т. с

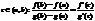
g(b)¹g(a) (неравны по теореме Ролля).

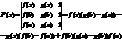
1). F(x) – непрерывна на [a,b]

2). F(x) – деффиренцирована на (a,b)

3). F(a)=0 ; F(b)=0

по теореме Ролля сущ. сÎ(a,b); F’(с)=0

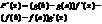
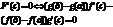
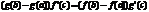
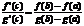
Асимптоты.

Опр. Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

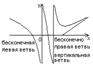
Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1: x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.

Теорема 2: Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при :

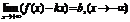
Док-во: Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

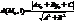
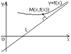Пусть y=kx+b

асимптота =>

d(M,l)®0=>

kx-f(x)+b®0

тогда f(x)-kx®b

при x®+µ

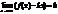существует предел:

Выпуклость графика функции.

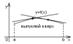Опр. График функции y=f(x) называется выпуклым вниз (вверх) если он расположен выше (ниже) любой касательной проведенной к графику функции на данном интервале.

Теорема: Достаточный признак выпуклости графика функции вниз.

Если функция f(x) дважды дефференц. на нтервале (a,b) и ее вторая производн. f’’(x)>0 на интервале (a,b), то график функции y=f(x) выпуклый вниз на интервале (a,b).

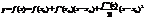Уравнение касательной:

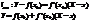
Возьмем X=x.Из первого вычтем второе

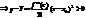
Поэтому y>Y следовательно график функции расположен выше касательной

Аналогично, если f’’(x)<0 на (a,b) то график функции y=f(x) - выпуклый вверх, на данном интервале.

Умножение матриц. Свойстваумножения.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы А_m×n на матрицу В_n×p, называется матрица С_m×p такая, что
с_ik = a_i1 × b_1k + a_i2 × b_2k + ... + a_in × b_nk,
т. е. находиться сумма произведений элементов i - ой строки матрицы А на соответствующие элементы j - ого столбца матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е - единичная матрица того же размера.

Свойства умножения матриц:Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка.
А × Е = Е × А = А

Умножение матриц обладает следующими свойствами:
1. А × (В × С) = (А × В) × С;
2. А × (В + С) = АВ + АС;
3. (А + В) × С = АС + ВС;
4. α × (АВ) = (αА) × В;
5. А × 0 = 0; 0 × А = 0;
6. (АВ)^Т = В^ТА^Т;
7. (АВС)^Т = С^ТВ^ТА^Т;
8. (А + В)^Т = А^Т + В^Т;