Умножение матриц, обратная матрица

Раздел 3. Матрицы.

1 Линейные операции над матрицами

2. Умножение матриц, обратная матрица

Линейные операции над матрицами.

Определение.Матрицей размера 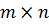(формата 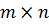) называется прямоугольная таблица чисел, содержащая 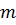строк и 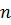столбцов.

Обозначаются матрицы заглавными латинскими буквами А, В, … . Числа, составляющие матрицу, называются элементами матрицы. В общем виде матрица размера 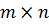выглядит следующим образом:

.

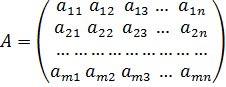Если хотят компактно указать, что матрица А имеет размер 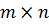, то записывают: 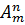или .

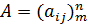Если число строк равно числу столбцов, то матрица называется квадратной. Для всякой квадратной матрицы А естественным образом можно составить и вычислить определитель этой матрицы, который обозначается :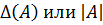

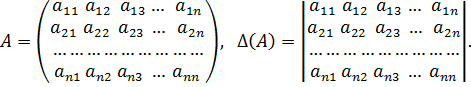
Замечание: нельзя «путать» скобки, - это не «мелочь»!!!

Если 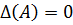, то матрица А называется особой (или вырожденной), если 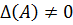, то неособой (невырожденной).

Матрица, сплошь состоящая из нулей, называется нулевой, обозначается .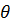

У всякой квадратной матрицы, как и у определителя, можно выделить две диагонали: главную (соединяющую левый верхний и правый нижний углы таблицы) и побочную.

Матрица называется диагональной, если у нее все элементы, кроме элементов стоящих на главной диагонали, равны нулю. Диагональная матрица называется единичной, если все элементы главной диагонали равны единице, обозначается Е. Ясно, что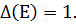

Рассмотрим далее операции (или действия), которые можно проводить с матрицами. Сначала рассмотрим линейные операции.

Во-первых, две матрицы называются равными, если они одинакового размера и все соответственные элементы (т.е. элементы, стоящие на одинаковых местах) равны.

Суммой двух матриц одинакового размера 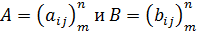называется матрица 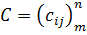, у которой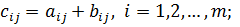

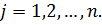Проще говоря, матрицы складываются поэлементно. Например:

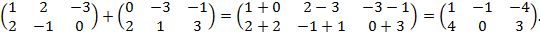
Произведениемчисла 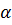на матрицу 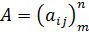называется матрица, у которой все элементы умножаются на это число: .

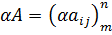Например: .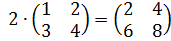

На практике этой операцией удобно пользоваться «в обратном направлении» - если все элементы матрицы имеют общий множитель, его можно вынести за знак матрицы в качестве сомножителя.

Заметим отличие этой операции над матрицами и над определителями!!!

Операции сложения матриц и умножения на число называются линейными операциями. Эти операции являются простейшими – для них справедливы основные законы операций – переместительный (коммутативный): 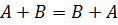; сочетательный (ассоциативный):

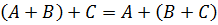и распределительный (дистрибутивны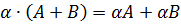й): и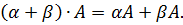

Следующая операция, умножение двух матриц, уже не столь проста.

Умножение матриц, обратная матрица.

Мы уже видели, что в матрице выделяют строки и столбцы. Матрица, состоящая из одной строки, называется матрицей – строкой. Матрица, состоящая из одного столбца, называется матрицей – столбцом. Поэтому ясно, что в матрице 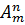можно выделить 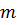строк. Все эти строки содержат 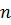элементов. Аналогично, такая матрица содержит 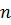столбцов, все они содержат 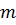элементов.

Определение.Произведением матрицы 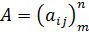на матрицу 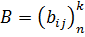называется такая матрица 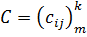, для которой выполняется:

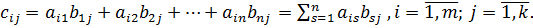(1)

Поясним на первый взгляд громоздкую формулу (1). Заметим, что в матрице 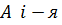строка имеет вид 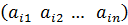, а в матрице 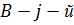столбец имеет вид

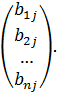
Теперь легко заметить, что формула (1) есть сумма произведений элементов 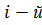строки первой матрицы на соответствующие элементы 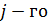столбца второй матрицы, т.е. скалярное произведение вектора –строки первой матрицы на вектор –столбец второй. Поэтому говорят, что матрицы умножают по правилу «строка на столбец».

Например,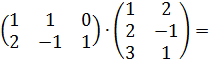

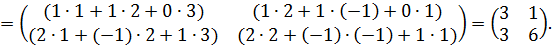
Надо немного «потренироваться» и умножение матриц не будет доставлять никаких трудностей.

Однако, из определения нетрудно заметить, что умножение матриц уже не обязательно удовлетворяет привычным для нас законам. Во – первых, из определения, т.е. из правила «строка на столбец», очевидно неравноправие сомножителей, поэтому ясно, что умножение матриц не обязательно перестановочно.

Пример 1. ;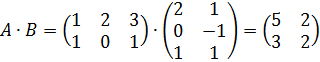

;

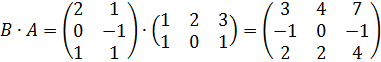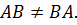
Пример 2.

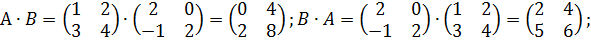
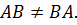
Пример 3.

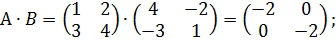
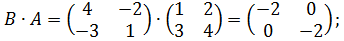
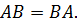
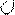
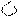Во – вторых, не всякие матрицы можно перемножить: ,

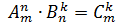- надо, чтобы количество столбцов первой матрицы равнялось количеству строк второй.

Пример 4.

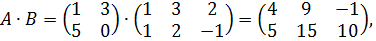
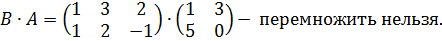
Квадратные матрицы одинакового порядка перемножить можно всегда. Для них вводим следующее понятие.

Определение.Квадратная матрица 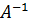называется обратной для матрицы А, если 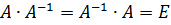, где 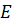– единичная матрица.

Отметим без доказательства, что для определителей матриц справедливо соотношение .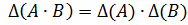

Пример 5.Проверим соотношение 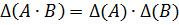для матриц

.

.

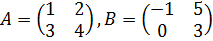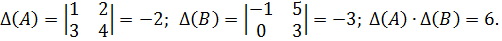
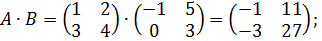
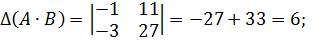
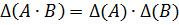Если это свойство применить к взаимно обратным матрицам, то получим, что 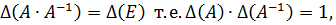т.к. определитель единичной матрицы равен единице. Из последней формулы следует, что 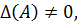а это означает, что обратная матрица существует лишь для неособых (невырожденных) матриц, а для вырожденных не существует.

Приведем без доказательства формулу для нахождения обратной матрицы:

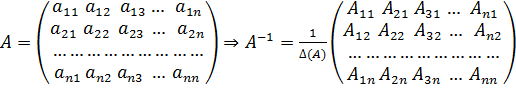(2)

Формула (2) вновь нам показывает, что 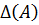стоит в знаменателе дроби и, следовательно, не может быть равным нулю. Кроме этого заметим, что элементами обратной матрицы являются алгебраические дополнения элементов матрицы 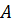, симметричных относительно главной диагонали (обратите внимание на индексы у элементов матрицы 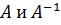, стоящих на одинаковых местах).

Определение.Если в матрице 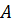все строки записать столбцами с теми же номерами, то такая операция называется транспонированием , а получившаяся матрица – транспонированной, она обозначается .

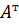Теперь можно переходить к примерам. Во избежание путаницы рекомендуется нахождение обратной матрицы проводить в следующем порядке. Пусть, например, имеется матрица 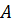третьего пордка.

.

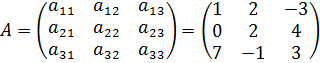1. Находим пределитель матрицы

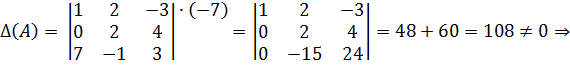
2. Находим алгебраические дополнения для каждого элемента матрицы

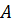, причем для удобства (во избежание упомянутой путаницы) располагаем их в том же порядке что и сами элементы матрицы 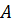(не забудем таблицу знаков!).

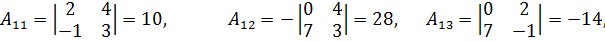
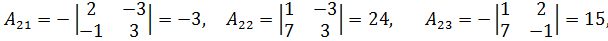
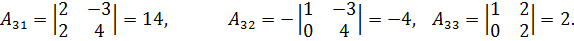
3. Записываем так называемую присоединенную матрицу

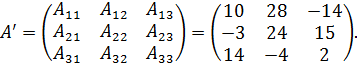
4. Для получения обратной матрицы остается протранспонировать присоединенную и поделить на :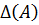

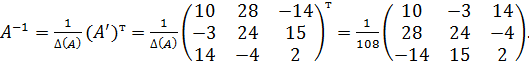
Разумеется, все выкладки («для первого раза») проведены излишне подробно. На практике этот пример оформляют значительно короче:

Начинаем в любом случае с вычисления 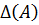, а далее:

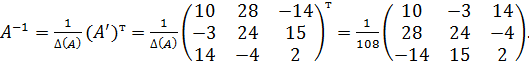
Вычисление алгебраических дополнений, т.е. определителей второго порядка ( с учетом таблицы знаков!), легко проводить «в уме» (устно).

Как видим, даже для матриц третьего порядка приходится проводить много арифметических подсчетов. Поэтому всегда полезно сделать проверку: должно выполняться 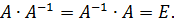Проверим:

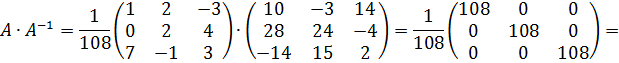
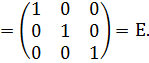
Пример 6. Даны матрицы .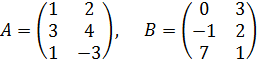

Найти матрицу .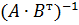

Решение. Сначала найдем матрицу

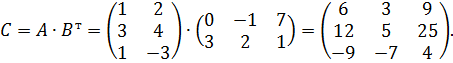
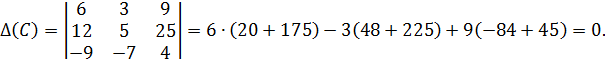
Ответ:Матрицы 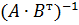не существует.

Матрицы и определители находят непосредственное применение в теории и практике систем линейных алгебраических уравнений (СЛАУ), к изучению которых мы и приступаем.