Теоремы о предельном переходе в неравенствах.

Теорема 1.Если " x f(x) £ g(x), то lim (x®x0) f(x) £ lim (x®x0) g(x)

Теорема 2.Пусть " x из окрестности точки x0 j(x) £ f(x) £ g(x) и lim (x®x0) j(x) = lim (x®x0) g(x) = a, тогда lim (x®x0) f(x) = a.

Сравнение бесконечно малых функций.

Функция a(x) называется бесконечно малой более высокого порядка,чем b(x) в окрестности точки x0, если lim (x®x0) a(x)/b(x) = 0.

Если бесконечно малые функции a(x) и b(x) имеют предел lim (x®x0) a(x)/b(x) = k ¹ 0 ¹ ¥, то a(x) и b(x) называют сравнимыми или одного порядка малости.

Если k = 1, то a(x) и b(x) – эквивалентные бесконечно малые.

Теорема.Сумма бесконечно малых функций эквивалента бесконечно малой низшего порядка.

Доказательство. Пусть есть a + b + g и g - низшего порядка.

a/g®0 и b/g®0, x®x0

lim (x®x0) a + b + g/g = lim (x®x0) a/g + b/g + 1 = 1

a + b + g ~ g

Функция f(x) называется бесконечно большойв окрестности точки x0, если предел в этой точке равен ± ¥/ lim (x®x0) f(x) = a

Функция f(x) – бесконечно большая Û 1/f(x) – бесконечно малая.

Для любых функций a(x) и b(x) с условием, что lim (x®x0) a(x)/b(x) = 0, пишут a(x) = o(b(x)) и говорят a(x) о-малое b(x), a(x) = O(b(x)) a(x) О-большое b(x).

Замечательные пределы.

1. lim (x®0) (sin x / x) = 1

2. lim (x®¥) (1 + 1/x)x = e = 2,7

Функция f(x)называется непрерывной в точке x0,если она определена в некоторой окрестности этой точки и lim (x®x0) f(x) = f(x0)

Теорема.Если функция f(x) и g(x) непрерывны в точке x0, то непрерывна функция f(x) ± g(x); f(x) * g(x); f(x)/g(x) (g(x) ¹ 0).

Точки разрыва.

1. Устранимый разрыв lim (x®x0 + 0) f(x) = lim (x®x0 - 0) f(x) + f(x0)

2. Разрыв первого рода – оба односторонних предела существуют, ¹ ¥ и ¹ между собой.

3. Разрыв второго рода – один из односторонних пределов не существует или равен ¥.

Функция f(x) называется непрерывной на замкнутом отрезке[a; b], если она непрерывна в каждой точке этого отрезка, а в точках a и b у нее существуют односторонние пределы.

M – максимальное значениефункции f(x) на отрезке [a; b], если " x Î [a; b] f(x) £ M

m – минимальное значениефункции f(x) на отрезке [a; b], если " x Î [a; b] f(x) ³ m

Теорема 1.Пусть f(x) непрерывна на отрезке [a; b], тогда она достигает свое наибольшее и наименьшее значение.

Теорема 2.Пусть f(x) непрерывна на отрезке [a; b], тогда она принимает все значения между наибольшим и наименьшим значениями.

" m £ C £ M $ x0 Î [a; b] f(x0) = C

Теорема 3.Пусть f(x) непрерывная на отрезке [a; b] принимает на концах этого отрезка значения разных знаков, тогда существует точка C Î [a; b] такая, что f(C) = 0.

Теорема 4.Если в окрестности точки x0 функция y(x) монотонна, то у нее существует обратная функция, которая непрерывна, если непрерывна функция y(x).

Производная.

Производной функции f(x1)называется lim (f(x1 + Dx) – f(x1)) / Dx = f ’(x1) = lim (Dx®0) Df / Dx, где Dx = x2 – x1 – приращение аргумента, Df = f(x2) – f(x1) – приращение функции.

Df / Dx = tg a ® tg j

Назовем линию L касательной к кривойy = f(x) в точке x0, если для любой секущей, проходящей через x0 и x1, секущая будет стремиться к L при x1®x0.

tg j - tg угла наклона касательной к кривой в точке x1 Þ k = tg j =

f ‘ (x1)

Правила дифференцирования.

1. (u ± v)’ = u’ ± v’

2. (u * v)’ = u’v + uv’

3. (u/v)’ = u’v – uv’/v²

Уравнение касательной:y – f(x0) = f ‘ (x0)(x – x0)

Уравнение нормали:y – f(x0) = (- 1/f ‘ (x0))*(x-x0)

Производная сложной функции.

Пусть z = f(y) и y = j(x) Þ z = f(j(x))

z’x = lim (Dx®0) Dz/Dx = lim (Dx®0) Dz/Dj * Dj/Dx = z’y * j’x

z’x = z’y + j’x

Производная обратной функции.Если функция у = f(x) и x = g(y) обратные, то y’x = 1/g’y.

Доказательство.

lim (Dx®0) Dy/Dx = lim (Dg®0) Dy/Dg = lim (Dg®0, Dy®0) 1/ (Dg/Dy) = 1/ g’y

Таблица производных:

1. a˟ - a˟ lna

2. loga x – 1/xlna

3. ln x – 1/x

4. sin x – cos x

5. cos x - -sin x

6. sh x – ch x

7. ch x – sh x

8. tg x – 1/cos² x

9. ctg x - -1/sin² x

10. arcsin x – 1/Ö1 - x²

11. arccos x - -1/Ö1 - x²

12. arctg x – 1/1+ x²

13. arcctg x - -1/1+ x²

14. e˟ - e˟

Функция 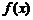называется дифференцируемой в точке 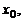если ее приращение 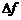в этой точке может быть представлено в виде

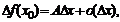
где .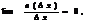

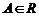Если приращение функции Df = f(x) – f(x0) можно представить в виде A(x – x0) +o(x – x0), то линейная часть A(x – x0) называется дифференциалом функции.

Свойства дифференциала:

1. d(f ± g) = df ± dg

2. d(f * g) = dfg + dgf

3. d(f/g) = (dfg – dgf)/g²

Доказательство.d(f +g) = (f + g)’dx = f’dx + g’dx = df + dg

Теорема.Если функция имеет дифференциал, то она имеет и производную, причем A = f’(x0).

Доказательство.Пусть функция имеет дифференциал Df = A(x – x0) + o(x - xo)

Df/Dx = A + o(x - xo)/ Dx

Пусть Dx®0 Þ f’(x0) = A

df = f’(x0)dx

С геометрической точки зрения дифференциал функции 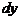равен приращению ординаты касательной к кривой 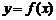в точке 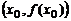, когда аргумент получает приращение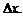

Пусть имеется функция f(j(x))

= y. Найдем дифференциал.

dy = (f(j(x)))’dx = f’ * j’(x) * dx = f’* dj

Последнее равенство называется свойством инвариантности дифференциала.