Предел функции на бесконечности.

Доказательство.

lim (n®¥) Xn = a Û " e > 0 $ N " n > N ½Xn - a½< e

Пусть e = 1

M = max {X1, X2, ..., Xn, a + 1} Þ Xn £ M " n.

m = min {X1, X2, ..., Xn, a - 1} Þ Xn ³ m " n.

Теорема.Если {Xn} монотонно возрастает, т.е. Xn+1 > Xn " n и ограничена сверху, то она имеет предел. Если {Xn} монотонно убывает, т.е. Xn+1 < Xn " n и ограничена снизу, то она имеет предел.

Доказательство.Xn убывает, Xn+1 < Xn " n $ m m £ Xn

Пусть m = inf {Xn} Û 1. " n m £ Xn 2. " e > 0 $ N XN < m + e

lim (n®¥) Xn = m Û " e > 0 $ N " n > N m £ Xn < XN < m + e Þ m - e £ Xn £ m + e.

Теорема о предельном переходе в неравенствах.Пусть lim (n®¥) Xn = a и lim (n®¥) Yn = b и пусть " n Xn £ Yn, тогда a £ b.

Доказательство.Пусть a > b, e = (a - b)/2 > 0.

" e > 0 $ N1 " n > N1 b - e < Yn < b + e

" e > 0 $ N2 " n > N2 a - e < Xn < a + e

Пусть n > max {N1;N2}

a - e < Xn £ Yn < b + e

a/2 + b/2 < a/2 + b/2 (противоречие)

Теорема о вложенных отрезках.Пусть есть система вложенных отрезков [a1;b1] É [a2;b2] É ... É [an;bn] ... Тогда существует точка C, принадлежащая всем отрезкам.

Доказательство.Последовательность a1, a2, ..., an убывает и " n an ³ b1, т.е. она имеет предел lim (n®¥) an = a.

Последовательность {bn} возрастает и bn £ a1, т.е. она имеет предел lim (n®¥) bn = b.

lim (n®¥) (an - bn) = 0 = b – a, т.е. a = b

C = a = b

" n an £ C £ bn, т.е. C принадлежит всем отрезкам.

Пусть даны два множества D и G. Если каждому элементу множества D ставится в соответствие единственный элемент множества G, то говорят, что задана функцияf: D ® G.

Если D = R и G = R, то функция числовая, если D = N и G = R, то функция последовательность.

Все функции, задаваемые с помощью знаков +, -, * и операцией взятия сложной функции от элементарных называются элементарными функциями.

Предел функции. По Коши:Число a называется пределом функции f (x) при x®x0 Û " e > 0 $ d > 0 " x 0 < ½x – x0½< d Þ ½f (x) - a½< e.

По Гейне:Число aназывается пределом функции f (x) при x®x0 Û " {Xn}®x0 Þ f (Xn)®a (n®¥).

Предел функции на бесконечности.

1. lim (x®x0) f(x) = ±¥

" E > 0 $ d > 0 " x 0 <½x – x0½< d Þ ½f(x)½> E ( для +¥ f(x) > E, для -¥ f(x) < -E)

2. lim (x®±¥) f(x) = a

" e > 0 $ D > 0 " x ½x½> D (для +¥ x > D, для -¥ x < -D)

Односторонние пределы.

Число a называется пределом слева(lim (x®x0 - 0) f(x) = a), если " e > 0 $ d > 0 " x x0 - d < x < x0 Þ ½f(x) - a½< e

Число a называется пределом справа(lim (x®x0 + 0) f(x) = a), если " e > 0 $ d > 0 " x x0 < x < x0 + d Þ ½f(x) - a½< e

Теорема.Если lim (x®x0) f(x) = a < ¥, то функция ограничена в некоторой окрестности точки x0.

Доказательство.

Пусть e = 1, тогда " x 0 <½x - x0½< d a - e < f(x) < a + e

Функция f(x) называется бесконечно малой в окрестности точки x0,если предел в этой же точке равен 0.

Теорема.Сумма бесконечно малых функций есть бесконечно малая функция.

Доказательство.lim (x®x0) a(x) = 0, lim (x®x0) b(x) = 0

" e/2 > 0 $ d1 > 0 " x 0 <½x – x0½< d1 Þ ½a(x)½< e/2

" e/2 $ d2 > 0 " x 0 <½x – x0½< d2 Þ ½b(x)½< e/2

" x 0 < ½x – x0½ < min (d1,d2) Þ ½a(x) + b(x)½< e Þ lim (x®x0) (a(x) + b(x)) = 0

Теорема.Если lim (x®x0) f(x) = b ¹ 0, то функция 1/f(x) ограничена в некоторой окрестности точки x0.

Доказательство.

Пусть b > 0, тогда " e = b/2 $ d " x 0 <½x – x0½< d Þ ½f(x) - b½< e

½b – f(x)½³ ½b½ - ½f(x)½

½b½ - ½f(x)½³ e = b/2

½f(x)½³ b/2

½1/f(x)½£ 2/b

Теорема.Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.

Доказательство. Пусть в окрестности точки x0 ½j(x)½£ M и lim (x®x0) a(x) = 0, тогда " e/M > 0 $ d > 0 "

x 0 <½x – x0½< d ½a(x)½< e/M

" e > 0 $ d > 0 " x 0 <½x – x0½< d ½a(x) - j(x)½< e/M * M < e

Теорема.Пусть lim (x®x0) f(x) = b ¹ 0 и a(x)(x®x0) ®0, тогда a(x)/f(x) бесконечно малая функция в окрестности точки x0.

Доказательство.1/f(x) – ограниченная, a*1/f(x) – бесконечно малая (по предыдущим теоремам).

Пусть lim (x®x0) f(x) = a и lim (x®x0) g(x) = b, тогда:

1. lim (x®x0) (f(x) ± g(x)) = a ± b

2. lim (x®x0) (f(x) * g(x)) = a * b

3. lim (x®x0) (f(x)/g(x)) = a/b (при b ¹ 0)

Теоремы о предельном переходе в неравенствах.

Теорема 1.Если " x f(x) £ g(x), то lim (x®x0) f(x) £ lim (x®x0) g(x)

Теорема 2.Пусть " x из окрестности точки x0 j(x) £ f(x) £ g(x) и lim (x®x0) j(x) = lim (x®x0) g(x) = a, тогда lim (x®x0) f(x) = a.

Замечательные пределы.

1. lim (x®0) (sin x / x) = 1

2. lim (x®¥) (1 + 1/x)x = e = 2,7

Функция f(x)называется непрерывной в точке x0,если она определена в некоторой окрестности этой точки и lim (x®x0) f(x) = f(x0)

Теорема.Если функция f(x) и g(x) непрерывны в точке x0, то непрерывна функция f(x) ± g(x); f(x) * g(x); f(x)/g(x) (g(x) ¹ 0).

Точки разрыва.

1. Устранимый разрыв lim (x®x0 + 0) f(x) = lim (x®x0 - 0) f(x) + f(x0)

2. Разрыв первого рода – оба односторонних предела существуют, ¹ ¥ и ¹ между собой.

3. Разрыв второго рода – один из односторонних пределов не существует или равен ¥.

Функция f(x) называется непрерывной на замкнутом отрезке[a; b], если она непрерывна в каждой точке этого отрезка, а в точках a и b у нее существуют односторонние пределы.

M – максимальное значениефункции f(x) на отрезке [a; b], если " x Î [a; b] f(x) £ M

m – минимальное значениефункции f(x) на отрезке [a; b], если " x Î [a; b] f(x) ³ m

Теорема 1.Пусть f(x) непрерывна на отрезке [a; b], тогда она достигает свое наибольшее и наименьшее значение.

Теорема 2.Пусть f(x) непрерывна на отрезке [a; b], тогда она принимает все значения между наибольшим и наименьшим значениями.

" m £ C £ M $ x0 Î [a; b] f(x0) = C

Теорема 3.Пусть f(x) непрерывная на отрезке [a; b] принимает на концах этого отрезка значения разных знаков, тогда существует точка C Î [a; b] такая, что f(C) = 0.

Теорема 4.Если в окрестности точки x0 функция y(x) монотонна, то у нее существует обратная функция, которая непрерывна, если непрерывна функция y(x).

Производная.

Производной функции f(x1)называется lim (f(x1 + Dx) – f(x1)) / Dx = f ’(x1) = lim (Dx®0) Df / Dx, где Dx = x2 – x1 – приращение аргумента, Df = f(x2) – f(x1) – приращение функции.

Df / Dx = tg a ® tg j

Назовем линию L касательной к кривойy = f(x) в точке x0, если для любой секущей, проходящей через x0 и x1, секущая будет стремиться к L при x1®x0.

tg j - tg угла наклона касательной к кривой в точке x1 Þ k = tg j =

f ‘ (x1)

Правила дифференцирования.

1. (u ± v)’ = u’ ± v’

2. (u * v)’ = u’v + uv’

3. (u/v)’ = u’v – uv’/v²

Уравнение касательной:y – f(x0) = f ‘ (x0)(x – x0)

Уравнение нормали:y – f(x0) = (- 1/f ‘ (x0))*(x-x0)

Доказательство.

lim (Dx®0) Dy/Dx = lim (Dg®0) Dy/Dg = lim (Dg®0, Dy®0) 1/ (Dg/Dy) = 1/ g’y

Таблица производных:

1. a˟ - a˟ lna

2. loga x – 1/xlna

3. ln x – 1/x

4. sin x – cos x

5. cos x - -sin x

6. sh x – ch x

7. ch x – sh x

8. tg x – 1/cos² x

9. ctg x - -1/sin² x

10. arcsin x – 1/Ö1 - x²

11. arccos x - -1/Ö1 - x²

12. arctg x – 1/1+ x²

13. arcctg x - -1/1+ x²

14. e˟ - e˟

Функция 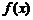называется дифференцируемой в точке 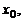если ее приращение 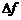в этой точке может быть представлено в виде

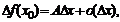
где .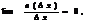

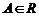Если приращение функции Df = f(x) – f(x0) можно представить в виде A(x – x0) +o(x – x0), то линейная часть A(x – x0) называется дифференциалом функции.

Свойства дифференциала:

1. d(f ± g) = df ± dg

2. d(f * g) = dfg + dgf

3. d(f/g) = (dfg – dgf)/g²

Доказательство.d(f +g) = (f + g)’dx = f’dx + g’dx = df + dg

Теорема.Если функция имеет дифференциал, то она имеет и производную, причем A = f’(x0).

Доказательство.Пусть функция имеет дифференциал Df = A(x – x0) + o(x - xo)

Df/Dx = A + o(x - xo)/ Dx

Пусть Dx®0 Þ f’(x0) = A

df = f’(x0)dx

С геометрической точки зрения дифференциал функции 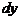равен приращению ординаты касательной к кривой 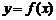в точке 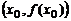, когда аргумент получает приращение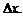

Пусть имеется функция f(j(x))

= y. Найдем дифференциал.

dy = (f(j(x)))’dx = f’ * j’(x) * dx = f’* dj

Последнее равенство называется свойством инвариантности дифференциала.

План исследования функции и построения графика

1. Найти область определения 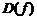функции .

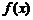2. Найти область значений 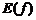(если это возможно вначале, часто 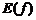можно указать только по результатам исследования).

3. Исследовать функцию на четность.

4. исследовать на периодичность.

5. Найти точки пересечения с осями Ox (нули функции) и Oy.

6. Найти промежутки знакопостоянства функции.

7. Исследовать на непрерывность, дать классификацию разрывов.

8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).

9. Исследовать на монотонность и экстремум.

10. Исследовать на выпуклость, вогнутость, перегиб.

11. Построить график функции.

На множестве X задана структура метрического пространства, если задана функция двух переменных, называемая метрикой, удовлетворяющая следующим аксиомам: r(x; y) = r(y; x); r(x; y) = 0 Û y = x; " x, y, z r(x; z) £ r(x; y) + r(y; z).

Множество D на плоскости назовем открытым, если оно содержит каждую свою точку вместе с некоторой окрестностью.

Назовем точку z Î D предельной, если в каждой ее окрестности есть точки из множества D.

Если множествоD содержит все свои предельные точки, то оно называется замкнутым.

Предел функции нескольких переменных.Число A называется lim (x®x0,y®y0) Û " e > 0 $ d-окрестность точки (x0; y0) " (x; y) Î d- окрестности (x ¹ x0 и y ¹ y0) ïf(x, y) - Aï < e.

Непрерывность функции нескольких переменных. Функция z = f(x, y) называется непрерывной в точке (x0; y0), если она определена в окрестности этой точки и lim (x®x0, y®y0) f(x, y) = f(x0, y0) (по любому пути).

Частные производные.Назовем частным приращением по xследующее выражение Dxf = f(x + Dx, y) – f(x, y) и частным приращением по y следующее выражение Dyf = f(x, y + Dy) – f(x, y).

Частной производной по xназывается lim (Dx®0) Dxf/Dx = ¶f/¶x (x, y) = f’x.

Частной производной по yназывается lim (Dy®0) Dyf/Dy = ¶f/¶y (x, y) = f’y.

Если дифференцируемая функция принимает выражение Df = f’yDy +f’xDx + a(x, y) + b(x, y), где a/ÖDx²+Dy² ® 0 и b/ÖDx²+Dy² ® 0, то выражение f’xdx + f’ydy называется полным дифференциалом функции f и обозначается df.

Касательная плоскость.Касательная плоскость, проходящая через точку M0 некоторой поверхности имеет следующее свойство: угол между этой плоскостью и любой секущей MM0 (M Î плоскости) ® 0, при M ® M0.

Уравнение нормали в каноническом виде: (x –x0)/ (¶f/¶x) = (y – y0)/ (¶f/¶y) = (z – z0)/ (¶f/¶z)

Функцияz = f(x, y) имеет локальный максимумв точке (x0, y0), если в окрестности этой точки значение f’(x – x0) > f(x, y) " (x, y).

Доказательство.

lim (n®¥) Xn = a Û " e > 0 $ N " n > N ½Xn - a½< e

Пусть e = 1

M = max {X1, X2, ..., Xn, a + 1} Þ Xn £ M " n.

m = min {X1, X2, ..., Xn, a - 1} Þ Xn ³ m " n.

Теорема.Если {Xn} монотонно возрастает, т.е. Xn+1 > Xn " n и ограничена сверху, то она имеет предел. Если {Xn} монотонно убывает, т.е. Xn+1 < Xn " n и ограничена снизу, то она имеет предел.

Доказательство.Xn убывает, Xn+1 < Xn " n $ m m £ Xn

Пусть m = inf {Xn} Û 1. " n m £ Xn 2. " e > 0 $ N XN < m + e

lim (n®¥) Xn = m Û " e > 0 $ N " n > N m £ Xn < XN < m + e Þ m - e £ Xn £ m + e.

Теорема о предельном переходе в неравенствах.Пусть lim (n®¥) Xn = a и lim (n®¥) Yn = b и пусть " n Xn £ Yn, тогда a £ b.

Доказательство.Пусть a > b, e = (a - b)/2 > 0.

" e > 0 $ N1 " n > N1 b - e < Yn < b + e

" e > 0 $ N2 " n > N2 a - e < Xn < a + e

Пусть n > max {N1;N2}

a - e < Xn £ Yn < b + e

a/2 + b/2 < a/2 + b/2 (противоречие)

Теорема о вложенных отрезках.Пусть есть система вложенных отрезков [a1;b1] É [a2;b2] É ... É [an;bn] ... Тогда существует точка C, принадлежащая всем отрезкам.

Доказательство.Последовательность a1, a2, ..., an убывает и " n an ³ b1, т.е. она имеет предел lim (n®¥) an = a.

Последовательность {bn} возрастает и bn £ a1, т.е. она имеет предел lim (n®¥) bn = b.

lim (n®¥) (an - bn) = 0 = b – a, т.е. a = b

C = a = b

" n an £ C £ bn, т.е. C принадлежит всем отрезкам.

Пусть даны два множества D и G. Если каждому элементу множества D ставится в соответствие единственный элемент множества G, то говорят, что задана функцияf: D ® G.

Если D = R и G = R, то функция числовая, если D = N и G = R, то функция последовательность.

Все функции, задаваемые с помощью знаков +, -, * и операцией взятия сложной функции от элементарных называются элементарными функциями.

Предел функции. По Коши:Число a называется пределом функции f (x) при x®x0 Û " e > 0 $ d > 0 " x 0 < ½x – x0½< d Þ ½f (x) - a½< e.

По Гейне:Число aназывается пределом функции f (x) при x®x0 Û " {Xn}®x0 Þ f (Xn)®a (n®¥).

Предел функции на бесконечности.

1. lim (x®x0) f(x) = ±¥

" E > 0 $ d > 0 " x 0 <½x – x0½< d Þ ½f(x)½> E ( для +¥ f(x) > E, для -¥ f(x) < -E)

2. lim (x®±¥) f(x) = a

" e > 0 $ D > 0 " x ½x½> D (для +¥ x > D, для -¥ x < -D)

Односторонние пределы.

Число a называется пределом слева(lim (x®x0 - 0) f(x) = a), если " e > 0 $ d > 0 " x x0 - d < x < x0 Þ ½f(x) - a½< e

Число a называется пределом справа(lim (x®x0 + 0) f(x) = a), если " e > 0 $ d > 0 " x x0 < x < x0 + d Þ ½f(x) - a½< e

Теорема.Если lim (x®x0) f(x) = a < ¥, то функция ограничена в некоторой окрестности точки x0.

Доказательство.

Пусть e = 1, тогда " x 0 <½x - x0½< d a - e < f(x) < a + e

Функция f(x) называется бесконечно малой в окрестности точки x0,если предел в этой же точке равен 0.

Теорема.Сумма бесконечно малых функций есть бесконечно малая функция.

Доказательство.lim (x®x0) a(x) = 0, lim (x®x0) b(x) = 0

" e/2 > 0 $ d1 > 0 " x 0 <½x – x0½< d1 Þ ½a(x)½< e/2

" e/2 $ d2 > 0 " x 0 <½x – x0½< d2 Þ ½b(x)½< e/2

" x 0 < ½x – x0½ < min (d1,d2) Þ ½a(x) + b(x)½< e Þ lim (x®x0) (a(x) + b(x)) = 0

Теорема.Если lim (x®x0) f(x) = b ¹ 0, то функция 1/f(x) ограничена в некоторой окрестности точки x0.

Доказательство.

Пусть b > 0, тогда " e = b/2 $ d " x 0 <½x – x0½< d Þ ½f(x) - b½< e

½b – f(x)½³ ½b½ - ½f(x)½

½b½ - ½f(x)½³ e = b/2

½f(x)½³ b/2

½1/f(x)½£ 2/b

Теорема.Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.

Доказательство. Пусть в окрестности точки x0 ½j(x)½£ M и lim (x®x0) a(x) = 0, тогда " e/M > 0 $ d > 0 "

x 0 <½x – x0½< d ½a(x)½< e/M

" e > 0 $ d > 0 " x 0 <½x – x0½< d ½a(x) - j(x)½< e/M * M < e

Теорема.Пусть lim (x®x0) f(x) = b ¹ 0 и a(x)(x®x0) ®0, тогда a(x)/f(x) бесконечно малая функция в окрестности точки x0.

Доказательство.1/f(x) – ограниченная, a*1/f(x) – бесконечно малая (по предыдущим теоремам).

Пусть lim (x®x0) f(x) = a и lim (x®x0) g(x) = b, тогда:

1. lim (x®x0) (f(x) ± g(x)) = a ± b

2. lim (x®x0) (f(x) * g(x)) = a * b

3. lim (x®x0) (f(x)/g(x)) = a/b (при b ¹ 0)