Применение кратных интегралов к вычислению площадей, объемов

Таким образом, с помощью n-кратного интеграла можно вычислять меру измеримых множеств в n-мерном пространстве (площадь — в двухмерном, объем — в трехмерном). Если n-кратный интеграл можно свести к повторному, то вычисление меры измеримого множества Е n-мерного пространства сведется к вычислению (n-1)-кратного интеграла.

Пусть, например, D — открытое измеримое множество в (n-1)-мерном пространстве и 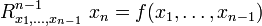— неотрицательная функция, определенная и непрерывная на замыкании 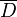, множества D, а G={x=(x₁…,x_n): (x₁…,x_n-1) ∈ D, 0< x_n < ƒ (x₁…,x_n-1) } (таким образом, G является n-мерным аналогом криволинейной плоской трапеции). Тогда
,
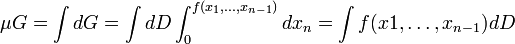то есть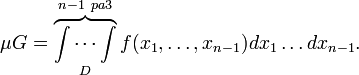
Меру произвольных (необязательно измеримых по Жордану), в частности неограниченных, открытых множеств пространства Rⁿ , n>=2, если её понимать как нижнюю меру Жордана μ _* , можно вычислить с помощью несобственных интегралов. Действительно пусть G — произвольное открытое множество в Rⁿ иG^k , k=1,2,…, — последовательность открытых измеримых множеств, монотонно исчерпывающих множество G. 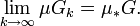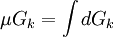Тогда, как известно, Но, , поэтому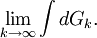

По определению же кратного несобственного интеграла, 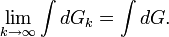Таким образом,

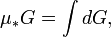
где интеграл в правой части равенства понимается, вообще говоря (а именно: если G не является измеримой областью), как несобственный.

Криволинейные интегралы 1 и 2 рода. Определение, вычисление.

Криволинейный интеграл первого рода

Свойства

1. Линейность: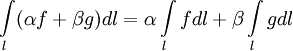

2. Аддитивность: если L₁∩L₂ в одной точке, то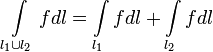

3. Монотонность: если f ≤gна l, то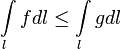

4. Теорема о среднем для непрерывной вдоль l функции f: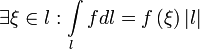

Очевидно, что: .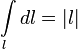

5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: .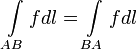

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

Вычисление

Пусть l — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция f(x,y,z) определена и интегрируема вдоль кривой l в смысле криволинейного интеграла первого рода. Тогда

.

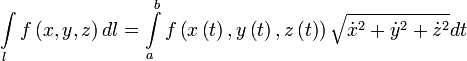Здесь точкой обозначена производная по t: x=x’(t)..

Криволинейный интеграл второго рода

Свойства

1. Линейность: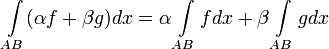

2. Аддитивность: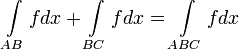

3. Монотонность: если f≤g на Γ, то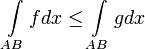

4. Оценка модуля: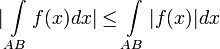

5. Теорема о среднем: если f непрерывна на Γ, то ∃M ∈Г, такая что: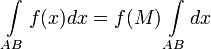
6.

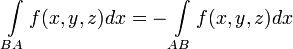
Вычисление

Пусть l — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция f(x,y,z) определена и интегрируема вдоль кривой l в смысле криволинейного интеграла второго рода. Тогда

, ,

.

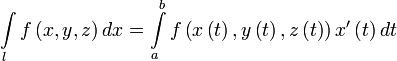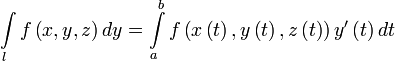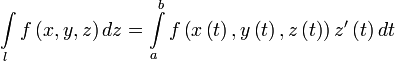Если обозначить за 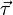касательный вектор к кривой l, то нетрудно показать, что

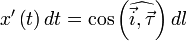
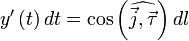
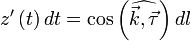
Формула Грина.

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция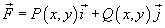

с непрерывными частными производными первого порядка 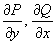. Тогда справедлива формула Грина 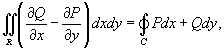- кривая C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.
Если Q=x, P=-y, то формула Грина принимает вид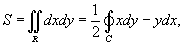

где S − это площадь области R, ограниченной контуром C.
Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией

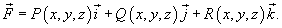
Ротором или вихрем векторного поля 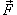называется вектор, обозначаемы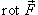й или 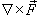и равный

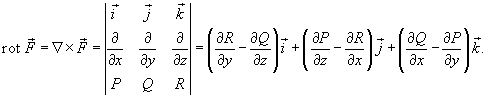
Формула Грина в векторной форме записывается в виде

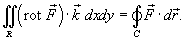
формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.