Применение производных к исследованию

Функция y=f(x), определенная на некотором отрезке [a, b] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [a, b] соответствует большее значение функции, то есть если x₁ < x₂, то f(x₁) < f(x₂).

Функцияy=f(x) убывающая на некотором отрезке [a, b], если меньшему значению аргумента x из [a, b]соответствует большее значение функции

x₁ < x₂, то f(x₁) > f(x₂).

Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.

Функция y=f(x) постоянная на некотором отрезке [a, b], если при изменении аргумента x она принимает одни и те же значения.

Рассмотрим график функции изображенной на рисунке и определим промежутки возрастания и убывания функции.

(-∞, a), (c, +∞) – убывает; (a, b) – постоянная; (b, c) – возрастает.

Применим понятие производной для исследования возрастания и убывания функции.

Теорема 1. (Необходимое и достаточное условия возрастания функции)

1. Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.

2. Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].

Доказательство.

1.Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и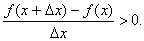

Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а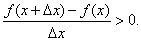

Переходя в этом равенстве к пределу при Δx→0, получим

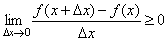, то есть f '(x)≥0.

2.Докажем вторую часть теоремы. Пусть f '(x)>0при всех x (a,b). Рассмотрим два любых значения x₁ и x₂ таких, что x₁ < x₂. Нужно доказать, что f(x₁)< f(x₂). По теореме Лагранжа существует такое число c  (x₁, x₂), что 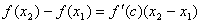. По условию f '(x)>0, x₁ – x₂>0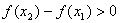 , а это и значит, что f(x) – возрастающая функция.

Аналогичная теорема имеет место и для убывающих функций.

Теорема 2. Если f(x) убывает на[a,b], то 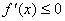на этом отрезке. Если 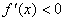на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b].

Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0.

Аналогично иллюстрируется и вторая часть теоремы.

Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания.

29. Теорема Ферма, Ролля . Если функция 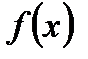непрерывное промежутке 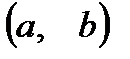, в некоторой внутренней точке 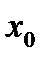этого промежутка достигает макси­мума (или минимума) и дифференцируема в этой точке, то ее произ­водная в этой точке равна нулю: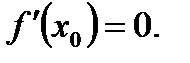

Доказательство. Предположим, что 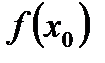есть наибольшее зна­чение; в случае, когда 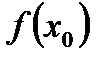— наименьшее значение, доказательство ана­логично.

При достаточно малых 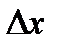[когда точка 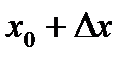принадлежит промежут­ку 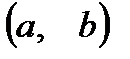] 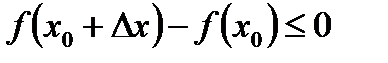независимо от знака 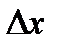, т. е. как для положи­тельных, так и для отрицательных 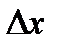. Деля на 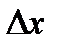, находим:

1) при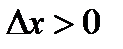

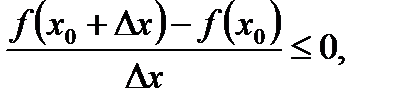
а переходя к пределу при 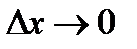, имеем в силу теоремы о пределе неполо­жительной переменной 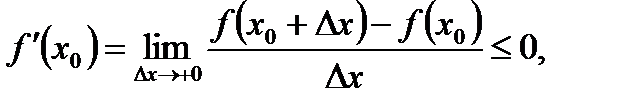(5.5) [предел существует и равен 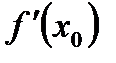, так как по условию функция дифферен­цируема в точке ];

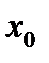2) при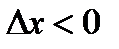

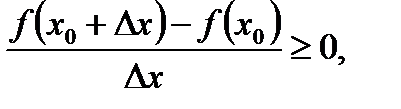
откуда, переходя к пределу при 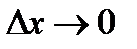, имеем в силу теоремы о пределе неотрицательной переменной 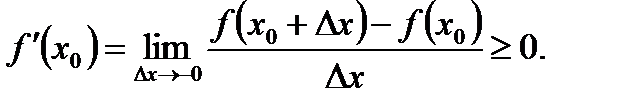(5.6)

Сравнивая полученные для 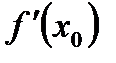неравенства (5.5) и (5.6), заключаем, что они оба будут удовлетворены только тогда, когда 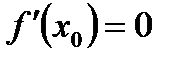. Тем самым теорема Ферма доказана. В частности, если точка 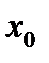есть точка строгого мак­симума 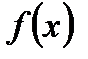), то все рассуждения остаются в силе, только будут иметь место строгие неравенства

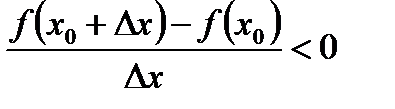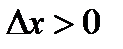при и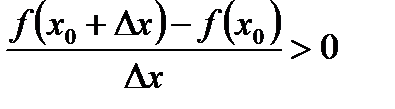

Геометрический смысл теоремы Ферма очевиден: касательная к графику функции 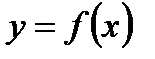в точке экстремума, в которой функция дифференцируема., параллельна оси.

2. Теорема Ролля. Если функция 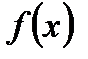непрерывна ,на отрезке 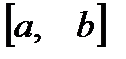, и дифференцируема в промежутке 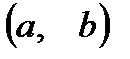и принимает на концах отрезка 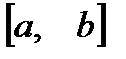равные значения 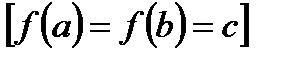, то в промежутке 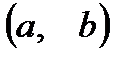найдется по крайней мере одна такая точка 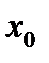, в которой производная будет равна нулю: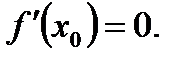

Доказательство. Прежде всего рассмотрим возможный по усло­виям теоремы случай, когда функция 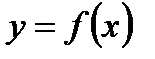сохраняет на отрезке 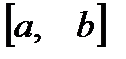по­стоянное значение: 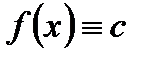_.В этом случае ее производная будет равна нулю во всех точках промежутка 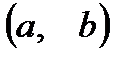: 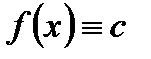, и, следовательно, теоре­ма верна для этого случая [точкой 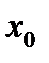является любая точка промежутка 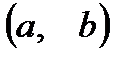].Если же 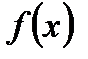не является постоянной на отрезке 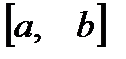, то, будучи не­прерывной на отрезке 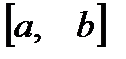, она достигает на нем своего наибольшего и наименьшего значени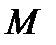й и 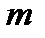.При соблюдении условий тео­ремы функция 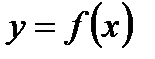может иметь в промежутке 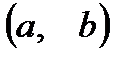и более чем две точки экстремума; во всех этих точках ее производная будет равна нулю. Геометричес­кий смысл теоремы Ролля: в услови­ях теоремы Ролля на графике функ­ции 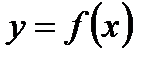найдется по крайней мере одна точка, в которой каса­тельная к графику будет параллель­на оси .

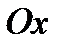Теорема Лагранжа, коши

Теорема Лагранжа Если функция f(x) непрерывна на отрезке [а, b] и дифференцируема в интервале (а,b), то существует такая точка с{а,b), что

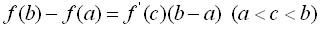
Следствие 1. Если производная функции равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная в этом промежутке.

Следствие 2. Если две функции имеют равные производные в некотором промежутке, то они отличаются в этом промежутке лишь постоянным слагаемым.

Корнем (или нулем) функции у = f(x) называется такое значение х = х0 ее аргумента, при котором эта функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось их или касается ее.

Теорема Коши: Если y = f(x) и у = у(х) - две функции, непрерывные на отрезке [а, b] и дифференцируемые в интервале (а, b) причем ф'(x) не равно 0 для любого х(а, b), то между а и b найдется такая точка с, что

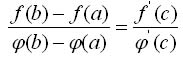
Экстремум функции

Функция 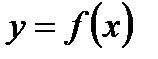называется возрастающей в промежутке 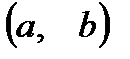, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует и большее значение функции.

Таким образом, если 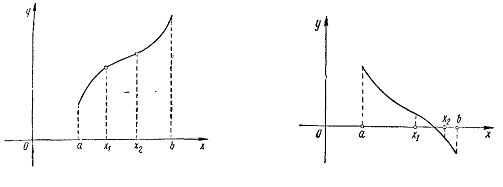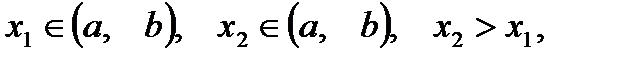то 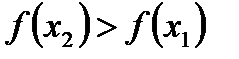Аналогично функция 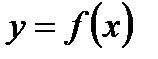называется убывающей в промежутке 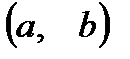, если для двух любых значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции.

Если 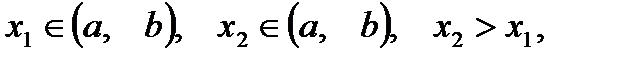то 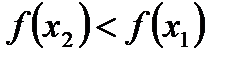Те значения аргумента, при которых функция достигает своих наиболь­ших или наименьших, по сравнению с соседними, значений, называются точками максимума и минимума.

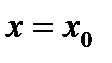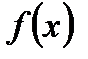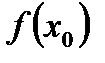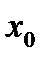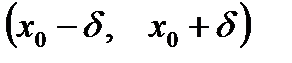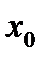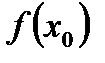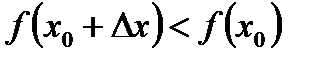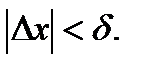Определение. Точка называ­ется точкой максимума функции , а значение называется максимумом этой функции, если существует некото­рая окрестность точки [т. е. проме­жуток ], такая, что зна­чение функции в любой точке этой ок­рестности будет меньше, чем ее значение в самой точке , т. е. меньше, чем максимум : при (5.3)

Аналогично(с заменой слова «меньше» на «больше») определяются точка минимума и минимум функции.Если 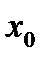— точка минимума, a 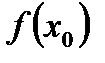мини­мум, то имеют место следующие неравенства:

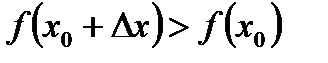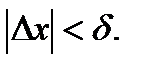при (5.4)

Максимум и минимум функции представлены на рис. 5.4 и 5.5.

Точки минимума и максимума объединяются под общим названием точек экстремума, а минимум и максимум функции объединяются общим названием экстремум функции.

Экстремумы функции 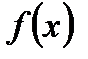, опреде­ленные выше с помощью неравенств (5.3) и (5.4), часто называются стро­гими экстремумами, в отличие от нестро­гих, где предполагаются неравенства вида 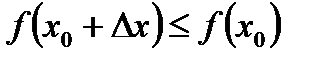и соответственно .

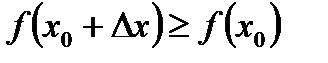Таким образом, понятия максимума и минимума функции носят харак­тер локальных (местных), а не абсолютных понятий.