Бесконечно малые величины, их свойства, эквивалентность.

Функция a(x) называется бесконечно малой при x®a, если 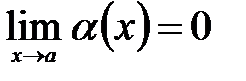, т.е. если для "e>0 существует d>0, что для всех 0<½x-а½<d, выполняется неравенство ça(x) ç<e. Бесконечно малую функцию ça(x) ç называют также бесконечно малой величиной.

Свойства бесконечно малых функций

1. Если функции a₁(x) и a₂(x) бесконечно малые, то сумма функций a₁(x)+ a₂(x) также есть бесконечно малая функция. Функция f(x) называется ограниченной при x®a, если существуют положительные числа М и d, такие, что при условии 0<½x-а½<d выполняется неравенство 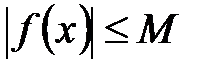.Любая бесконечно малая функция a(x) является ограниченной функцией при x®a.

2. Произведение ограниченной при x®a функции на бесконечно малую, есть функция бесконечно малая.

3. Произведение постоянной на бесконечно малую есть бесконечно малая.

4. Произведение двух бесконечно малых есть бесконечно малая функция.

Раскрытие неопределённостей

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

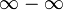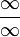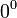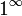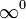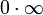по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов 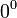, , 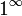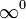пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

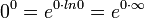
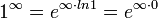
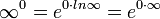
Для раскрытия неопределённостей типа 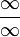используется следующий алгоритм:

Выявление старшей степени переменной;

Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа существует следующий алгоритм:

Разложение на множители числителя и знаменателя;

Сокращение дроби.

Для раскрытия неопределённостей типа 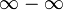иногда удобно применить следующее преобразование:

Пусть 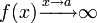и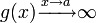

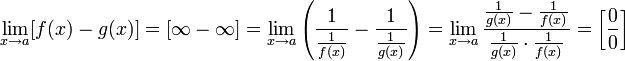
20. Непрерывность функции.Основные определения, теоремы

Пусть y=f(x) определена в некотором интервале (а, b), x₀ и x – два произвольных значениях аргумента из этого интервала. Обозначим x–x₀=Dx откуда x=x₀+Dx. Говорят, что для перехода от значения аргумента x₀ к значению x, первоначальному значению придано приращение Dx.

Приращением Dy функции y=f(x), соответствующем приращению Dx аргумента x в точке x₀, называется разность D y=f (x₀ +Dx)-f (x₀)

Определение. Функция y=f(x) называется непрерывной в точке x₀, если бесконечно малому приращению Dx аргумента x в точке x₀ соответствует бесконечно малое приращение функции D y т.е.

Определение. Если функция непрерывна в каждой точке отрезка [а, b], то она непрерывна на этом интервале. Теорема 1. Если функции f₁ (x) и f₂ (x) непрерывны в точке x₀, то непрерывны в этой точке также их алгебраическая сумма f₁(x)± f₂(x), произведение f₁(x) f₂(x) и при условии f₂(x₀)≠0 частное 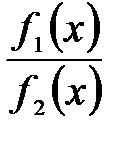(аналогично теоремам о пределах).

Теорема 2. Если функция u=j(x) непрерывна в точке x₀, а функция y=f(u) непрерывна в точке u₀=j(x₀), то сложная функция y=f(j(x)) непрерывна в точке x₀.

Точки разрыва

Функция f(x) называется непрерывной в точке х₀, если: 1) она определена в этой точке; 2) существует 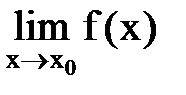; 3) этот предел равен значению функции в точке х₀, т.е. 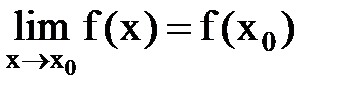.Если хотя бы одно из этих трёх условий не выполняется, то функция называется разрывной в точке х₀, а сама точка х₀ называется точкой разрыва функции.

Классификация точек разрыва

Различают следующие виды разрывов:

1)устранимый разрыв

2)разрыв первого рода или скачок

3)разрыв второго рода

Разрывы первого и второго рода неустранимы