Вычисление полной вероятности.
Перестановки элементов множества. Число перестановок. Примеры вычисления.
Перестановкой множества из 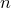 элементов называется расположение элементов в определенном порядке.
элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов 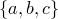 — это
— это
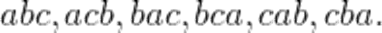
Очевидно, перестановки можно считать частным случаем размещений при 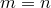 .
.
Число всех перестановок из 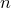 элементов обозначается
элементов обозначается 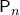 (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
(от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
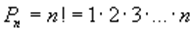
(восклицательным знаком обозначается факториал)
Пример.Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки 8 ладей

Пример 2:
Сколькими способами можно переставить 5 различных книг на книжной полке?
Решение:
Порядок расположения элементов важен, элементы не повторяются. Используем число перестановок.
5!=1·2·3·4·5=12
Пример 3:
Сколько различных чисел можно составить из цифр 0, 1, 2, 3, если ни одна из цифр не будет повторяться?
Решение:
Всего цифр четыре. Если бы среди заданных цифр не было нуля, задача решалась бы аналогично предыдущей:
4!=1·2·3·4=24 различных числа.
Но на первом месте не может стоять ноль. Таких вариантов 3! = 6 (0123, 0132, 0213, 0231, 0312, 0321). Поэтому количество чисел: 4!-3! = 24-6 = 18
Перестановки с повторениями. Примеры.
Пусть даны 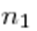 элементов первого типа,
элементов первого типа, 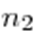 — второго типа, ...,
— второго типа, ..., 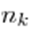 —
— 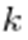 -го типа, всего
-го типа, всего 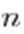 элементов. Способы разместить их по
элементов. Способы разместить их по 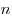 различным местам называются перестановками с повторениями. Их количество обозначается
различным местам называются перестановками с повторениями. Их количество обозначается 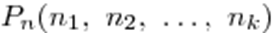 .
.
Теорема: число перестановок с повторениями есть
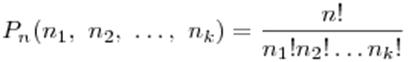 .
.
3.Размещения элементов множества и их вычисление. Примеры.
Размещениями множества из 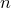 различных элементов по
различных элементов по 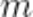 элементов
элементов  называются комбинации, которые составлены из данных
называются комбинации, которые составлены из данных 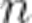 элементов по
элементов по 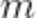 элементов и отличаются либо самими элементами, либо порядком элементов.
элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из 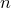 элементов по
элементов по 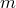 элементов обозначается через
элементов обозначается через 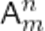 (от начальной буквы французского слова “arrangement”, что означает размещение), где
(от начальной буквы французского слова “arrangement”, что означает размещение), где 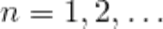 и
и  .
.
Теорема. Число размещений множества из 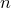 элементов по
элементов по 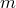 элементов равно
элементов равно
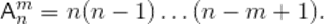
Пример.Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
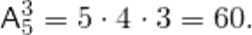
Сочетания элементов множества. Число сочетаний. Примеры вычисления.
Сочетаниями из 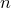 различных элементов по
различных элементов по 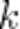 элементов называются комбинации, которые составлены из данных
элементов называются комбинации, которые составлены из данных 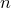 элементов по
элементов по 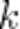 элементов и отличаются хотя бы одним элементом (иначе говоря,
элементов и отличаются хотя бы одним элементом (иначе говоря, 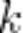 -элементные подмножества данного множества из
-элементные подмножества данного множества из 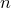 элементов).
элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из 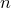 элементов по
элементов по 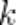 элементов в каждом обозначается
элементов в каждом обозначается 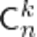 (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
(от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа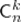

Все сочетания из множества 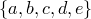 по два —
по два — 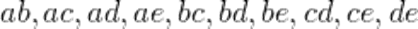 .
.
 .
.
Теорема. 
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
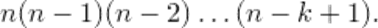
2 способ. Выберем сначала 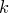 элементов из данного множества, а затем расположим их в некотором порядке
элементов из данного множества, а затем расположим их в некотором порядке
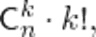
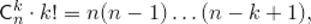
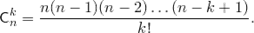
Домножим числитель и знаменатель этой дроби на  :
:
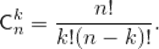
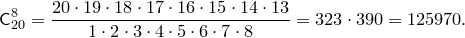
Пример.Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
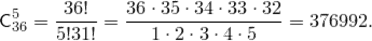
Вероятность. Классическая формула вычисления вероятности. Примеры с игральной костью и монетами.
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта в котором может появиться это событие.
Вероятность события А обозначают через Р(А) (здесь Р - вероятность). В соответствии с определением Р(А)= m/n , (1.2.1)
где m - число элементарных исходов, благоприятствующих событию А;
n -число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Вероятность события имеет следующие свойства:
1. Вероятность достоверного события равна единице. Обозначим достоверное событие буквой U. Для достоверного события m =n, поэтому
P(U) = 1. (1.2.2)
2. Вероятность невозможного события равна нулю. Обозначим невозможное событие буквой V. Для невозможного события m = 0, поэтому
P(V) =0. (1.2.3)
3. Вероятность случайного события выражается положительным числом, меньшим единицы: Поскольку для случайного события А выполняются неравенства 0 <m<n, или 0<m/n< 1, то
0<Р(А)<I. (1.2.4)
4. Вероятность любого события В удовлетворяет неравенствам
0 ≤ Р(В) ≤1. (1.2.5)
Это следует из соотношений (1.2.2) и (1.2.4).
Пример 1. Подбрасываются две симметричные монеты. Чему равна вероятность того, что на верхних сторонах обеих монет оказались цифры?
Решение: Обозначим буквой D событие "на верхней стороне каждой монеты оказалась цифра". В этом испытании 4 равновозможных элементарных исходов: (Г, Г), (Г, Ц), (Ц, Г), (Ц, Ц). (Запись (Г, Ц) означает, что на первой монете герб, на второй - цифра). Событию D благоприятствует один элементарный исход (Ц, Ц). Поскольку m = 1, n = 4 , то P(D)=1/4-=0,25.
Пример2 Подбрасывается два игральных кубика, отмечается число очков на верхней грани каждого кубика. Найти вероятность того, что на обоих кубиках выпало одинаковое число очков.
Решение:Обозначим это событие буквой - А. Событие А благоприятствуют 6 элементарных исходов: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6).
Всего равновозможных элементарных исходов, образующих полную группу событий, в данном случае n=62=36. Значит, искомая вероятность
Р(А) = 6/36 =1/6 ≈ 0,167.
Частота событий. Статистическая вероятность. Примеры вычислений.
Относительной частотой события, или частотой, называется отношение числа опытов, в которых появилось это событие, к числу всех
произведенных опытов. Обозначим частоту события А, через W(A), тогда по определению
W(A)=m/n, (1.4.1)
где m - число опытов, в которых появилось событие А; n - число всех произведенных опытов.
Частота события обладает следующими свойствами.
1. Частота случайного события есть число, заключенное между нулем и единицей:
0<W(A)< 1. (1.4.2)
2. Частота достоверного события U равна единице:
W(U) = 1. (1.4.3)
3. Частота невозможного события V равна нулю:
W(V)=0. (1.4.4)
4. Частота суммы двух несовместных событий А и В равна сумме частот этих событий:
W(A + В) = W(A) + W(B) . (1.4.5)
Наблюдения позволяют установить, что относительная частота обладает свойствами статистической устойчивости: в различных сериях многочленных испытаний (в каждом из которых может появиться или не появиться это событие) она принимает значения, достаточно близкие к некоторой постоянной. Эту постоянную, являющуюся объективной
числовой характеристикой явления, считают вероятностью данного события.
Вероятностью события называется число, около которого группируются значения частоты данного события в различных сериях большого числа испытаний. Это определение вероятности называется статистическим.
В случае статистического определения вероятность обладает следующими свойствами: 1) вероятность достоверного события равна единице;
2) вероятность невозможного события равна нулю;
3) вероятность случайного события заключена между нулем и единицей;
4) вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Пример 1. Игральный кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова частота появления шестерки?
Решение: Из условия задачи следует, что n = 60, m = 10, поэтому W=10/60=1/6.
Пример 2. Проведены три серии многократных подбрасываний симметричной монеты, подсчитаны числа появлений герба:
1) n1 = 4040, m1=2048,
2)n2=12000, m2=6019;
3)n3=24000, m3=12012. Найти
частоту появления герба в каждой серии испытаний.
Решение:. В соответствии с формулой (1.4.1) находим:
W1 = m1/n1 = 2048/4040 = 0,5069;
W2= m2/n2 = 6019/1200 ≈ 0,5016;
W3 = m3/n3 = 12012/24000 ≈ 0,5005.
Геометрическая вероятность (линейный, плоский и объемный случаи). Примеры.
Геометрические вероятности - вероятности попадания точки в область. Пусть Ω — ограниченное множество пространства имеющее объем λ(Ω) пусть ω — точка, взятая случайным образом из Ω, пусть вероятность, что точка будет взята из подмножества 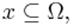 пропорциональна его объёму λ(x), тогда геометрическая вероятность подмножества
пропорциональна его объёму λ(x), тогда геометрическая вероятность подмножества 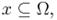 определяется как отношение объёмов:
определяется как отношение объёмов:
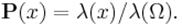
Для плоского случая определяется как отношение площадей:
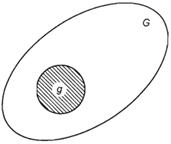
P(A) = SG/Sg
В общем случае понятие геометрической вероятности вводится следующим образом. Обозначим меру области (длину, площадь, объем)
через mesg, а меру области G - через mesG (тes - первые три буквы французского слова mesure, что значит мера); обозначим буквой А событие "попадание брошенной точки в области g, которая содержится в области G". Вероятность попадания в область g точки, брошенной в область G, определяется формулой^
Р(А) = mesg /mesG
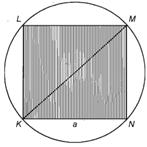
Пример: В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность того, что точка попадет в квадрат?
Решение. Введем обозначения: R - радиус круга,
а - сторона вписанного квадрата, А - попадание точки в квадрат, S - площадь круга, S1 -
площадь вписанного квадрата. Как известно, площадь круга S = πR2 Сторона вписанного квадрата через радиус описанной окружности вы-
ражаетсяформулой а = 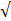 2R , поэтому площадь квадрата S1 = 2R2, соответственно P(A) =
2R , поэтому площадь квадрата S1 = 2R2, соответственно P(A) = 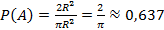
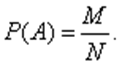 8.Три определения вероятности(классической, статистической, геометрической).
8.Три определения вероятности(классической, статистической, геометрической).
Классическое определение вероятности.
Возможностью или благоприятным случаем называют случай, когда при реализации определённого комплекса обстоятельств события А происходят. Классическое определение вероятности предполагает напрямую вычислить число благоприятных случаев или возможностей.
Вероятностью события А называют отношение числа благоприятных этому событию возможностей к числу всех равновозможных несовместимых событий N, которые могут произойти в результате одного испытания или наблюдения:
Если совершенно понятно, о вероятности какого события идёт речь, то тогда вероятность обозначают маленькой буквой p, не указывая обозначения события.
Чтобы вычислить вероятность по классическому определению, необходимо найти число всех равновозможных несовместимых событий и определить, сколько из них благоприятны определению события А.
Статистическая вероятность.
В определении статистической вероятности используется понятие относительно частоты события А. Относительной частотой события А называют отношение числа наблюдений, в которых наблюдается А, к числу всех наблюдений. Относительную частоту обычно обозначают буквой W. Если в n наблюдениях событие А наблюдается m раз, то относительная частота события А:
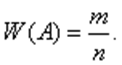
Геометрическая вероятность.
Если число исходов некоторого опыта бесконечно, то классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события 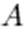 есть отношение меры
есть отношение меры 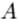 (длины, площади, объема) к мере
(длины, площади, объема) к мере 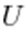 пространства элементарных событий.
пространства элементарных событий.
Зависимые и независимые события. Условная вероятность. Умножение вероятностей зависимых событий. Примеры.
События А, Б, В... называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий. События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них.
Условной вероятностью (РA (В)-условная вероятность события В относительно А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. пример условной вероятности Условная вероятность события В при условии, что событие А уже наступило, по определению, равна РA (В) = Р (АВ) / Р (А) (Р(A)>0).
Умножения вероятностей зависимых событий: вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р (АВ) = Р (А) РA (В)
Пример. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.
Решение:Вероятность того, что первый валик окажется конусным (событие A), Р (А) = 3 / 10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность РA (В) = 7 / 9.
По формуле умножения, искомая вероятность Р (АВ) = Р (А) РA (В) = (3 / 10) * (7 / 9) = 7 / 30. Заметим, что, сохранив обозначения, легко найдем: Р (В) = 7 / 10, РB (А) = 3 / 9, Р (В) РB (А) = 7 / 30
Условие независимости событий. Умножение вероятностей независимых событий. Примеры.
Событие В не зависит от события А, если
Р(В/А) = Р(В) т.е. вероятность события В не зависит от того, произошло ли событие А.
В этом случае и событие А не зависит от события В, тоесть свойство независимости событий является взаимным.
Вероятность произведения двух независимых событий равна произведению их вероятностей:
Р(АВ) = Р(А)Р(В) .
Пример 1: Прибор, работающий в течение времениt, состоит из трех узлов, каждый из которых, независимо от других, может в течение времени t отказать (выйти из строя). Отказ хотя бы одного узла приводит к отказу прибора в целом. За время t надежность (вероятность безотказной работы) первого узла равна p1= 0,8; второго p2 = 0,9 третьего p3 = 0,7. Найти надежность прибора в целом.
Решение. Обозначая:
A – безотказная работа приборов,
A1 - безотказная работа первого узла,
A2- безотказная работа второго узла,
A3 - безотказная работа третьего узла,
имеем:
A = A1A2A3
откуда по теореме умножения для независимых событий
P(A) = P(A1)P(A2)P(A3) = p1p2p3 = 0,504
Пример 2. Найти вероятность совместного появления цифры при одном подбрасывании двух монет.
Решение. Вероятность появления цифры первой монеты (событие А) Р(А) = 1/2; вероятность появления цифры второй монеты (событие В)- Р(В) = 1/2.
События А и В независимы, поэтому искомую вероятность найдем
по формуле:
Р(АВ) = Р(А)Р(В) = 1/2 *1/2 = 1/4
Совместность и несовместность событий. Сложение вероятностей двух совместных событий. Примеры.
Два события называются совместными, если появление одного из них не влияет и не исключает появление другого. Совместные события могут реализоваться одновременно, как, например, появление какого-либо числа на одной кости ни
коим образом не влияет на появление чисел на другой кости. События несовместны, если в одном явлении или при одном испытании они не могут реализоваться одновременно и появление одного из них исключает появление другого (попадание в цель и промах несовместны).
Вероятность появления хотя бы одного из двух совместных событий A или B равна сумме вероятностей этих событий без вероятности их совместного появления:
P(A+B) = P(A)+P(B)-P(AB).
Пример. Вероятность попадания в мишень для первого спортсмена 0,85, а для второго - 0,8. Спортсмены независимо друг от друга
сделали по одному выстрелу. Найти вероятность того, что в мишень попадет хотя бы один спортсмен?
Решение. Введем обозначения: события А - "попадание первого спортсмена", В - "попадание второго спортсмена", С -"попадание хотя бы одного из спортсменов". Очевидно, А + В = С, причем события А и В совместны. В соответствии с формулой получаем:
P(C) = Р(А) + Р(В) - Р(АВ)
Р(C) = Р(А)+ Р(В)-Р(А)Р(В),
поскольку А и В - независимые события. Подставив данные значения Р(А) = 0,85, Р(В) = 0,8 в формулу для Р( C) , найдем искомую вероятность
Р(С) = (0,85 + 0,8) - 0,85·0,8 = 0,97
Несовместные события. Сложение вероятностей несовместных событий. Примеры.
События несовместны, если в одном явлении или при одном испытании они не могут реализоваться одновременно и появление одного из них исключает появление другого (попадание в цель и промах несовместны).
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Пример 1. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение. Появление цветного шара означает появление либо красного, либо синего шара.
Вероятность появления красного шара (событие А)
Р (А) = 10 / 30 = 1 / 3.
Вероятность появления синего шара (событие В)
Р (В) = 5 / 30 = 1 / 6.
События А и В несовместны (появление шара одного цвета исключает появление шара другого цвета).
Искомая вероятность
P (A + B) = P (A) + P (B) = l / 3 + l / 6 = l / 2.
Пример 2. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую — 0,35. Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
Решение. События А — "стрелок попал в первую область" и В — "стрелок попал во вторую область" — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима.
Искомая вероятность
Р (А + В) = Р (А) + Р (В) = 0,45 + 0,35 = 0,80
Вероятность в полной группе событий. Примеры
События A1, А2… Аn образуют полную группу событий, если AjAk = ∅ (i≠k) и А1 + А2 + ... + Аn = Ω .
Где ∅ - невозможное событие (вероятность равна 0)
Ω - достоверное событие (вероятность равна 1)
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта в котором может появиться это событие.
Вероятность события А обозначают через Р(А) (здесь Р - вероятность). В соответствии с определением Р(А)= m / n
где m - число элементарных исходов, благоприятствующих событию А;
n -число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Пример: Консультационный пункт института получает пакеты с контрольными работами из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В — 0,2. Найти вероятность того, что очередной пакет будет получен из города С.
Решение. События "пакет получен из города А", "пакет получен из города В", "пакет получен из города С" образуют полную группу, поэтому сумма вероятностей этих событий равна единице:
0,7 + 0,2 + p =1.
Отсюда искомая вероятность
р = 1 — 0,9 = 0,1.
Вероятность противоположных событий.Примеры
Событие 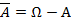 называется противоположным событию А; событие
называется противоположным событию А; событие 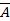 означает, что событие А не произошло.
означает, что событие А не произошло.
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта в котором может появиться это событие.
Вероятность события А обозначают через Р(А) (здесь Р - вероятность). В соответствии с определением Р(А)= m / n
где m - число элементарных исходов, благоприятствующих событию А;
n -число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Пример 1. Попадание и промах при выстреле по цели — противоположные события. Если А — попадание, то противоположное событие — промах.
Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противоположные.
Примеры.
Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,
A = H1A + H2A + … + HnA
Применяя аксиому сложения вероятностей, имеем
P(A) = P(H1A + H2A + … + HnA) = P(H1A) + P(H2A) + … + P(HnA)
но P(HiA) = P(Hi)PHi(A)(i=1, 2, ..., n), поэтому
P(A) = P(H1)PH1(A) + P(H2)PH2(A) + … + P(Hn)PHn(A)
Или
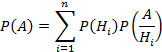
Эта формула называется формулой полной вероятности. События H1, H2, ..., Hn часто называют «гипотезами».
Пример.В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов?
Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны:
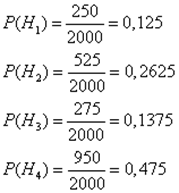
Далее, из условия задачи следует, что:
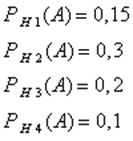
Используя формулу полной вероятности, имеем:
P(A) = 0,125*0,15+0,2625*0,3+0,1375*0,2 + 0,475*0,1 = 0,1725
Дискретные и непрерывные случайные величины. Примеры.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
| F (х) = Р(Х < х ). | (5.1) |
где х – произвольное действительное число.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение s(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
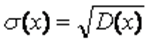 . . | (5.2) |
Далее рассматриваются отличия между дискретной и непрерывной случайными величинами.
Формула Бернулли вычисления вероятности. Примеры
Опыты α1, α2,… называются независимыми, если любая комбинация их исходов является совокупностью независимых событий. В вероятностной схеме Бернулли рассматривается последовательность n независимых опытовα1, α2,… αnв каждом из которых некоторое событие A может наступить с одной и той же вероятностью p= P(A). Условно это событие рассматривается как успех, а его ненаступление (событие  ) – как неудача. Вероятность неудачи q = 1 - p в каждом опыте равна.
) – как неудача. Вероятность неудачи q = 1 - p в каждом опыте равна.
Пусть для заданного целого числа k (0 ≤ k ≤ n) Pn(k) обозначает вероятность того, что в n опытах успех наступит ровно k раз. Имеет место формула Бернулли:
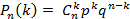
Вероятности Pn(k) (k = 0,1,…, n) называются биномиальными в силу того, что правая часть формулы представляет собой общий член разложения бинома Ньютона:
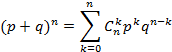
Так как p + q = 1, то из формулы бинома Ньютона следует, что сумма всех биномиальных вероятностей равна 1:
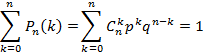
Пример 1. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0.8 и не зависит от номера выстрела. Требуется найти вероятность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень
Решение. В этом примере n = 5, р = 0.8 и k = 2; по формуле Бернулли находим:
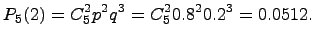
Пример 2. Вероятность попадания в мишень при одном выстреле для данного стрелка 0,7 и не зависит от номера выстрела. Найти вероят
ность того, что при 5 выстрелах произойдет ровно 2 попадания в мишень.
Решение. Поскольку р = 0,7, то q = 1 - p = 1 - 0,7 = 0,3. По условию n = 5, k = 2, по формуле находим
P5(2) = C52p2q5-2 = 10 *(0,7)2 * (0,3)3 = 0,1323
Формула Пуассона вычисления вероятности. Примеры
В одинаковых условиях производится n независимых испытаний, в каждом из которых может появиться событие А с вероятностью р или событие 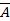 с вероятностью q (q = 1 - р). Вероятность того, что при n испытаниях событие А появится k раз (ине появится n - k раз) определяется формулой Бернулли
с вероятностью q (q = 1 - р). Вероятность того, что при n испытаниях событие А появится k раз (ине появится n - k раз) определяется формулой Бернулли
Рассмотрим случай, когда n является достаточно большим, а р - достаточно малым; положим nр = а, где а - некоторое число.
Распределением Пуассона называется распределение вероятностей дискретной случайной величины, определяемое формулой:
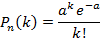
Постоянную a=np, входящую в формулу называют параметром распределения Пуассона.
Закон распределения Пуассона можно записать в виде следующей таблицы:
| X | … | k | … | |||
| P | e-a | ae-a | 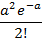 | … | 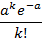 | … |
Пример 1. На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.
Решение. Дано: n = 100000, p = 0,0001, m = 3 (m = 5).
a=np=10
Воспользуемся формулой Пуассона
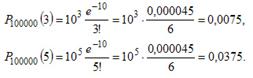
Пример 2. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времениТ равна 0,002. Найти вероятность того, что за времяТ откажут ровно три элемента.
Решение. По условию дано: n=10000, p = 0,002, a=np = 2, k =3
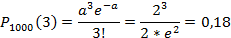
21.Математическое ожидание случайной величины.
МО -характеризует среднее взвешенное значение случайной величины.
Для вычисления математического ожидания для ДСВ каждое значение xi учитывается с «весом», пропорциональным вероятности этого значения.
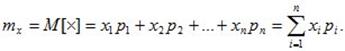 (6.1)
(6.1)
M[X]-оператор математического ожидания;
mx-- число, полученное после вычислений по формуле.
Для НСВ заменим отдельные значения 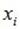 непрерывно изменяющимся параметром
непрерывно изменяющимся параметром 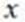 , соответствующие вероятности
, соответствующие вероятности 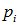 - элементом вероятности
- элементом вероятности 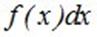 , а конечную сумму – интегралом:
, а конечную сумму – интегралом: 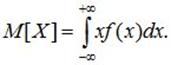 (6.2)
(6.2)
Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами 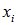 , в которых сосредоточены соответственно массы р1, р2,...., причем
, в которых сосредоточены соответственно массы р1, р2,...., причем 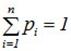 . Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью
. Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью 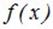 .
.
Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.
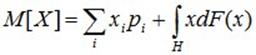 , (6.3)
, (6.3)
где сумма распространяется на все значения xi, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна.
Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.
Перестановки элементов множества. Число перестановок. Примеры вычисления.
Перестановкой множества из 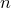 элементов называется расположение элементов в определенном порядке.
элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов 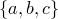 — это
— это
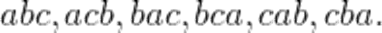
Очевидно, перестановки можно считать частным случаем размещений при 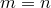 .
.
Число всех перестановок из 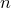 элементов обозначается
элементов обозначается 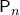 (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
(от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
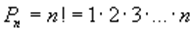
(восклицательным знаком обозначается факториал)
Пример.Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки 8 ладей

Пример 2:
Сколькими способами можно переставить 5 различных книг на книжной полке?
Решение:
Порядок расположения элементов важен, элементы не повторяются. Используем число перестановок.
5!=1·2·3·4·5=12
Пример 3:
Сколько различных чисел можно составить из цифр 0, 1, 2, 3, если ни одна из цифр не будет повторяться?
Решение:
Всего цифр четыре. Если бы среди заданных цифр не было нуля, задача решалась бы аналогично предыдущей:
4!=1·2·3·4=24 различных числа.
Но на первом месте не может стоять ноль. Таких вариантов 3! = 6 (0123, 0132, 0213, 0231, 0312, 0321). Поэтому количество чисел: 4!-3! = 24-6 = 18
Пе
