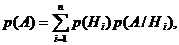Где N – общее число опытов, М – число появлений события А.
Статистической вероятностью события считают его относительную частоту или число, близкое к ней.
Замечание 1. Из формулы следует, что свойства вероятности, доказанные для ее классического определения, справедливы и для статистического определения вероятности.
Замечание 2. Для существования статистической вероятности события А требуется:
возможность производить неограниченное число испытаний;
Устойчивость относительных частот появления А в различных сериях достаточно большого числа опытов.
Замечание 3. Недостатком статистического определения является неоднозначность статистической вероятности.
Основные формулы комбинаторики. Размещения, сочетания, перестановки
Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок
Рп = п! (1.3)
Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений
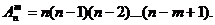
Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний
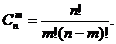
5)
6) Теорема умножения вероятностей. Зависимые и независимые события. Условная вероятность
(теорема умножения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:
р (АВ) = р (А) · р (В/А). (2.6)
Доказательство.
Воспользуемся обозначениями теоремы 2.1. Тогда для вычисления р(В/А) множеством возможных исходов нужно считать тА (так как А произошло), а множеством благоприятных исходов – те, при которых произошли и А, и В ( тАВ ). Следовательно,
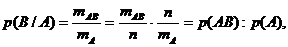откуда следует утверждение теоремы.
Назовем условной вероятностью р(В/А) события В вероятность события В при условии, что событие А произошло.
Замечание. Понятие условной вероятности используется в основном в случаях, когда осуществление события А изменяет вероятность события В.
Событие В называется независимым от события А, если появление события А не изменяет вероятности В, то есть р (В/А) = р (В).
Замечание. Если событие В не зависит от А, то и А не зависит от В. Действительно, из (2.7) следует при этом, что р (А) · р (В) = р (В) · р (А/В), откуда р (А/В) = р (А). Значит, свойство независимости событий взаимно.
Теорема умножения для независимых событий имеет вид:
р (АВ) = р (А) · р (В)
7)Теорема сложения вероятностей совместимых событий.
(теорема сложения). Вероятность р(А + В) суммы событий А и В равна
Р (А + В ) = р (А) + р (В) – р (АВ). (2.2)
Доказательство.
Докажем теорему сложения для схемы случаев. Пусть п – число возможных исходов опыта, тА – число исходов, благоприятных событию А, тВ – число исходов, благопри-ятных событию В, а тАВ – число исходов опыта, при которых происходят оба события (то есть исходов, благоприятных произведению АВ). Тогда число исходов, при которых имеет место событие А + В, равно тА + тВ – тАВ (так как в сумме (тА + тВ) тАВ учтено дважды: как исходы, благоприятные А, и исходы, благоприятные В). Следовательно, вероятность суммы можно определить по формуле (1.1):
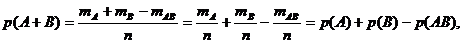
Что и требовалось доказать.
Следствие 1. Теорему 2.1 можно распространить на случай суммы любого числа событий. Например, для суммы трех событий А, В и С
Р(А + В + С) = р(А) + р(В) + р(С) – р(АВ) – р(АС) – р(ВС) + р(АВС) (2.3)
И т.д.
Следствие 2. Если события А и В несовместны, то тАВ = 0, и, следовательно, вероятность суммы несовместных событий равна сумме их вероятностей:
Р(А + В) = р(А) + р(В).
8) Формула полной вероятности и формула Байеса. Произведение событий.
Вероятность события А, наступающего совместно с гипотезами Н1, Н2,…, Нп, равна:
