Общая схема исследования функции и построения графика

Асимптоты графика функции

Асимптотой кривой на­зывается прямая, расстояние до которой от точки, лежащей на кривой, стремится к ну­лю при неограниченном удалении от начала координат этой точки по кривой. Асимптоты могут быть вертикальными, наклонными и горизонтальными.

Говорят, что прямая х = а является вер­тикальной асимптотой графика функции у = f(х), если 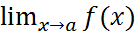=∞, или 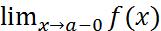=∞, или =∞.

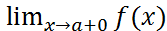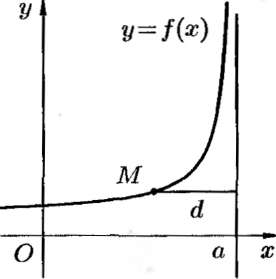
Горизонтальная асимптота — прямая вида при условии существования предела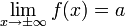

Наклонная асимптота — прямая вида при условии существования пределов

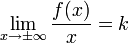
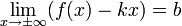
Общая схема исследования функции и построения графика

Исследование функции у=f(x) целесообразно вести в определен­ной последовательности.

1. Найти область определения функции.

2. Найти (если это можно) точки пересечения графика с осями координат.

3. Найти интервалы знакопостоянства функции (промежутки, на которых f(x) > 0 или f(x) < 0).

4. Выяснить, является ли функция четной, нечетной или общего вида.

5. Найти асимптоты графика функции.

6. Найти интервалы монотонности функции.

7. Найти экстремумы функции.

8. Найти интервалы выпуклости и точки перегиба графика функ­ции.

На основании проведенного исследования построить график функ­ции.

Глобальный экстремум на отрезке

Наибольшее и наименьшее значения непрерывной функции f на отрезке [a;b] называются глобальным max и min соответственно или глобальным экстремумом. Глобальный экстремум существует в силу теоремы Вейерштрасса. Ясно, что точками глобального экстремума могут быть точки локального экстремума или концы отрезка. Отсюда правило отыскания глобального экстремума непрерывной функции f на отрезке[a;b]:

1) Находим точки возможного экстремума на интервале (a,b)

2) Вычисляем значение функции f в этих точках и значения f(a), f(b)

Наибольшее из этих значений есть , а наименьшее -

Предел функции в точке, непрерывность ф.м.п.

Пусть функция z=f(x;y) определена в некоторой окрестности точки Мо(Xо;Yо), кроме, быть может, самой этой точки. Число А называется пределом функции z=f(x;y) при х→Xо и у→Yо (или, что то же самое, при М(х;у)→Мо(Xо;Yо)), если для любого ε> 0 существует > 0 такое, что для всех х Xо и у у₀ и удовлетворяю­щих неравенству < выполняется неравенство <ε. Записывают:

или

Функция z = f(x;у) (или f(М)) называется непрерывной в точ­ке Мо(хо;уо), если она:

а)определена в этой точке и некоторой ее окрестности,

б)имеет предел ,

в) этот предел равен значению функции z в точке М₀, т. е.

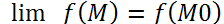
Функция z = f(x;у) называется непрерывной в точке М₀(X₀;Y₀) D, если выполняется равенство ,т. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов x и у стремятся к нулю.

Локальные экстремумы ф.м.п.

Точка (хо;уо) называется точкой максимума функции z = f(х;у), если существует такая -окрестность точки (Xо; Yо), что для каждой точки (x; у), отличной от (хо;уо), из этой окрестности вы­полняется неравенство f(x; у) < f(Xо;Yо).Аналогично определяется точ­ка минимума функции: для всех точек (x; у), отличных от (Xо;Yо), из -окрестности точки (Xо;Yо) вы­полняется неравенство: f(x;у) >f(Xо;Уо).Значение функции в точке мак­симума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функ­ции называют ее экстремумами.

Дифференцируемость ф.м.п. Примеры применения частных производных в экономике.

Функция f(x, y) дифференцируема в точке (x0, y0) (или сокращенно 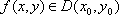), если справедливо равенство:

(1) f(x, y)=f(x0, y0) + A(x - x0) + B(y - y0) +0(p) где 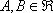- некоторые константы, а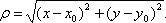

Зафиксируем одну из переменных, например: y=y0. Тогда f(x0, y0) будет функцией от x и равенство (1) примет вид: f(x0, y)=f(x0, y0) + A(x - x0) + B(y - y0) + o(x - x0). Следовательно, число A есть производная функции f(x0, y) в точке x=x0. Эта производная обозначается так: 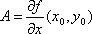и называется частной производной f(x, y) по x в точке (x0, y0). Аналогично: 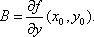Таким образом условие дифференцируемости функции f(x, y) в точке (x0, y0) можно представить в виде:

f(x, y)=f(x0, y0) + 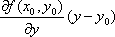+0(p). В экономических исследованиях часто используется производственная функция Кобба-Дугласа 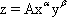, где z - величина общественного продукта, x - затраты труда, y - объем производственных фондов (обычно z и y измеряются в стоимостных единицах, x - в человеко-часах); A, a, b - постоянные.

Применение в экономическом анализе. Базовой задач экон анализа явл изучение связей эконом величин, записан в виде функй.

В экон-ке очень часто требуется найти наил или оптим значение показателя: наив производ-ть труда, макс прибыль, макс выпуск, мин издержки и т. д. Каждый показатель представляет собой функ от одного или неск-х аргументов.

Условный экстремум функции нескольких переменных. Метод множителей Лагранжа. Наибольшее и наименьшее значения непрерывной функции в замкнутой области.Найти экстремум z, при ксловии, что x и y связаны следующим образом.

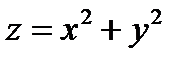; x+y-1=0;

(*)

; ; ;

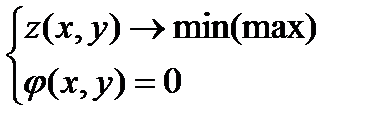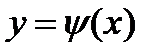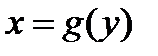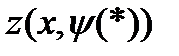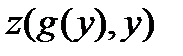
Метод множителя Ла-Гранджа.

(*) эквивалентна задач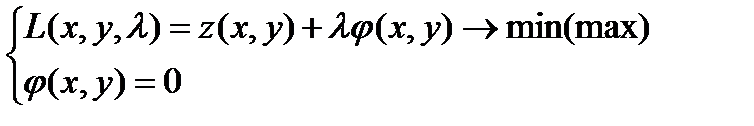е: , где

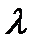-множитель Ла-Гранджа; 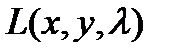- функция Ла-Гранджа.

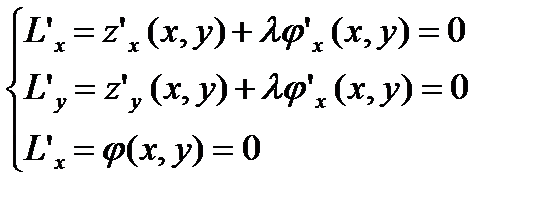
Надо исследовать 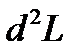ф-ции Ла-Гранджа с учетом условия связи в диффиринциалах.

Наибольшее и наименьшее значение ф-ции в замкнутой области.

Если ф-я определена в замкнутой ограниченной области Д, то она достигает своего min и max значения, либо в стационарных точках внутри области, либо на ее границе.

25. Опред опред интеграла \. Геом и физич интерпретация опред интеграла

Это — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Пусть на отрезке [a,b] задана функ y = f(x). Разобьём отрезок [a,b] произвольным образом на n частей точками [x0 , x1], [x1 , x2], …, [xi-1 , xi], …, [xn-1 , xn]; длину i-го отрезка обозначим 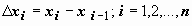макс из длин отрезков обозначим 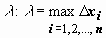На каждом из отрезков [xi-1 , xi] выберем произвольную точку и составим

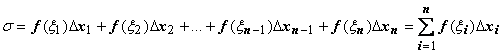
Сумма 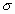наз интегральной суммой. Если сущ-т (конечный) предел последов-ти интеграл сумм 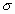при 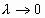не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек , то функция f(x) наз-ся интегрир. по отрезку [a,b], а этот предел наз-ся определ. Интегр. от функ. f(x) по отрез. [a,b] и обозначается 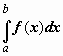это есть опред интеграл

Геометрический смысл

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Фолрмула Ньютона-Лейбница

Формула Ньютона — Лейбница или теорема анализа даёт соотношение между двумя операциями: взятием определ. интеграла и вычислением первообразной.

Если 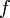непрерывна на отрезке 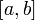и 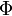— ее любая первообразная на этом отрезке, то имеет место равенство

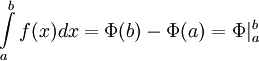
27. Свойства определенного интеграла

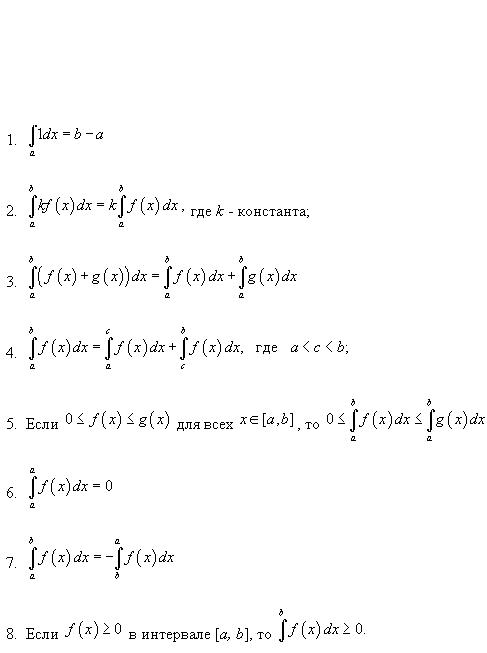
Асимптоты графика функции

Асимптотой кривой на­зывается прямая, расстояние до которой от точки, лежащей на кривой, стремится к ну­лю при неограниченном удалении от начала координат этой точки по кривой. Асимптоты могут быть вертикальными, наклонными и горизонтальными.

Говорят, что прямая х = а является вер­тикальной асимптотой графика функции у = f(х), если 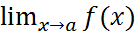=∞, или 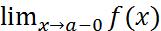=∞, или =∞.

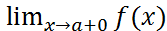Горизонтальная асимптота — прямая вида при условии существования предела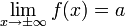

Наклонная асимптота — прямая вида при условии существования пределов

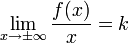
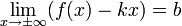
Общая схема исследования функции и построения графика

Исследование функции у=f(x) целесообразно вести в определен­ной последовательности.

1. Найти область определения функции.

2. Найти (если это можно) точки пересечения графика с осями координат.

3. Найти интервалы знакопостоянства функции (промежутки, на которых f(x) > 0 или f(x) < 0).

4. Выяснить, является ли функция четной, нечетной или общего вида.

5. Найти асимптоты графика функции.

6. Найти интервалы монотонности функции.

7. Найти экстремумы функции.

8. Найти интервалы выпуклости и точки перегиба графика функ­ции.

На основании проведенного исследования построить график функ­ции.