Предел функции в точке. Теорема о пределе суммы, разности, произведения и частного.

Функция f(x) имеет предел A в точке Xo , предельной для области определения функции f(x) , если для каждой окрестности предела A существует проколотая окрестность точки Xo , образ которой при отображении f(x) является подмножеством заданной окрестности точки A.

Говорят,что число b – есть предел ф-цииf(x)при х->а, то limf(x) {x->a} = b.

Свойства пределов функции:

1) Предел постоянной величины:предел постоянной величины равен самой постоянной величине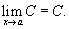

2) Предел суммы:Предел суммы двух функций равен сумме пределов этих функции 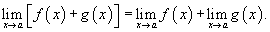Предел суммы нескольких функций равен сумме пределов этих функций.Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину: постоянный коэффициэнт можно выносить за знак предела: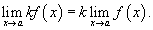

4) Предел произведения: предел произведения двух функций равен произведению пределов этих функций.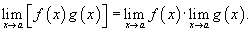

5)Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: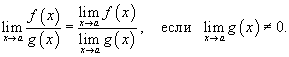

Первый и второй замечательный предел.

Первый и второй замечательный предел используют для раскрытия неопределенностей, содержащих тригонометрические функции

Первый замечательный предел.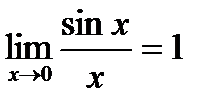

Второй замечательный предел.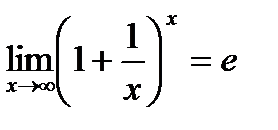

Эквивалентность бесконечно малых функций

Бесконечно малые функцииα(x) иβ(x) называются эквивалентными при x 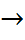a, если
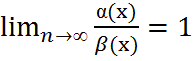. Если α(х) – бесконечно малая функция, то справедливы основные эквивалентности: sinα(x)~α(x); tgα(x)~α(x);arcsinα(x)~ α(x); arctgα(x)~α(x); e^α(x) 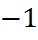~α(x); ln(1+α(x))~α(x); a^α(x) 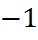~α(x)*lnα; 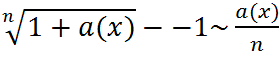. При вычислении пределов используются следующие теоремы об эквивалентных бесконечно малых функциях:

Т1) Предел отношения двух бесконечно малых функций равен пределу отношения функций, им эквивалентных,

Т2) Сумма нескольких бесконечно малых функций различных порядков малости эквивалентна слагаемому низшего порядка малости.

Непрерывность функции и классификация точек разрыва

Функция у=f(x) называется непрерывной в точке 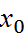, если она определена некоторой окрестностью этой точки и предел 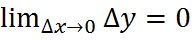. Cгеометрической точки зрения непрерывность функции означает, что график функции не имеет «разрывов»

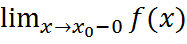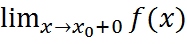Точки разрыва можно разбить на 2 класса: а)1-го рода, для которых и существуют, но не равны f(x₀); б) 2-го рода, для которых хотя бы один из пределов 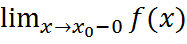или 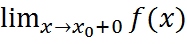не существует или бесконечен.

Производная

Пусть функция у=f(x) определена в некоторой окрестности точки х0, если переменная х получит приращение ∆х, то переменная у получит приращение ∆у=∆у(х0)= ∆f(х0)=f(х0+∆х)-f(х0)

Опр.1 Производной функции у=f(x) в т. х0 называется =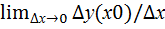

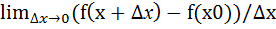
Производная функции f(x) в т. х обознач. у’=у’(x)=f’(x)= df/dx=dy/dx

При каждом конкретном значении х производная (если она сущ.) представляет собой некоторое число, таким образом конечному знач. х ставится в соотв. f’(x). Полученая функция как бы произведена от f(x). Этим объясняется понятие производной.

Операция нахождения производной назыв. дифференцированием.

Пусть кривая l является гр. функц. у=f(x) и точка М0(х0;f(x0))принадл. L. Рассмотрим некоторую секущую М0М

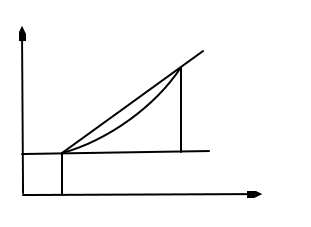
Угловой коэффициент секущей tgɸ=∆y/∆x, если т. М движ. По кривой в т. М0, то сек. М0М стемится к некоторому предельному положению наз.касательной, угловой коэф. Которой К= 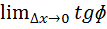= =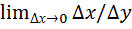y’(x0).

Таким образом геометрич. смысл произв. следующий: производная ф. в т. х0 ровна угл. Коэф. Косательной и гр. функции у=f(x) в т. х0: y-f(x0)=f’(x0)(x-x0)

Cмеханич. Точки зрения произв. ф. представляет собой мгновенную скорость процесса. Например произв. пути по времени- скорость, произвскороти- ускорение.

Опр 2: Функция y=f(x) назыв. дифференцируемой в т. х0, если она имеет в т х0 конечную произв.

Функция назыв. Дифференцируемой, если она дифф. В каждой точке интервала.

Т1: Если функция f(x) диффер в т. х0 то она в этой точке непрерывна.

Док-во: 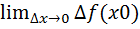= = 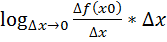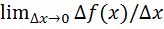* 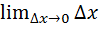=f’(x0)*0

Замечание: Утверждение обратное т1 не имеет места. Например у= 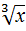непрерывна в т. х=0, но не фифференцируема или ф. у= 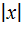непрерывна в т. х=0, но не дифф. В ней.

Дифференциал функции

Под дифференциалом функцииdy функцииy=f(x) понимается главная часть её приращения ∆у, пропорциональная приращению ∆х независимой х.

Дифференциалdx независимой переменной х равен её приращению dx=∆x.

Дифференциал любой дифференцируемой функцииy=f(x) равен произведению её производной на дифференциал независимой переменной dy=f’(x)dx

Из формулы dy=f’(x)dxвытекает представление производ. в виде частного двух дифференциаловf‘(x)=dy/dx

Если ∆х достаточно мало по модулю, то с точностью до бесконечно малых более высокого порядка малости, чем ∆х, имеет место приближённое равенство ∆у≈dy или

f(x+∆x)≈f(x)+f’(x)*∆x

Соотношение f(x+∆x)≈f(x)+f’(x)*∆xиспользуют в приближённых вычислениях.