Вывод канонических уравнений эллипса, гиперболы, параболы.

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.

Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

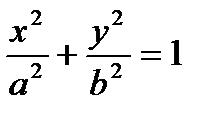- уравнение эллипса.

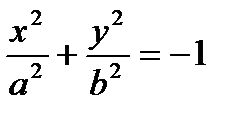- уравнение “мнимого” эллипса.

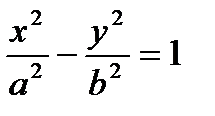- уравнение гиперболы.

a²x² – c²y² = 0 – уравнение двух пересекающихся прямых.

y² = 2px – уравнение параболы.

y² – a² = 0 – уравнение двух параллельных прямых.

y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

y² = 0 – пара совпадающих прямых.

(x – a)² + (y – b)² = R² – уравнение окружности.

Окружность:

(x – a)² + (y – b)² = R² центр имеет координаты (a; b).

Эллипс.

Эллипсом называется кривая, заданная уравнением .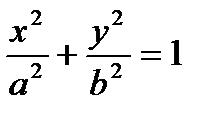

Фокусаминазываются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;b – малая полуось.

Теорема.Фокусное расстояние и полуоси эллипса связаны соотношением:

a² = b² + c².

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r₁ + r₂ = 2 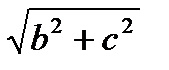(по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r₁ + r₂ = a – c + a + c. Т.к. по определению сумма r₁ + r₂ – постоянная величина, то , приравнивая, получаем:

a² = b² + c²

r₁ + r₂ = 2a.

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

е = с/a.

Т.к. с <a, то е < 1.

Определение. Величина k = b/a называется коэффициентом сжатияэллипса, а величина 1 – k = (a – b)/a называется сжатиемэллипса.

Гипербола.

Гиперболойназывается множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.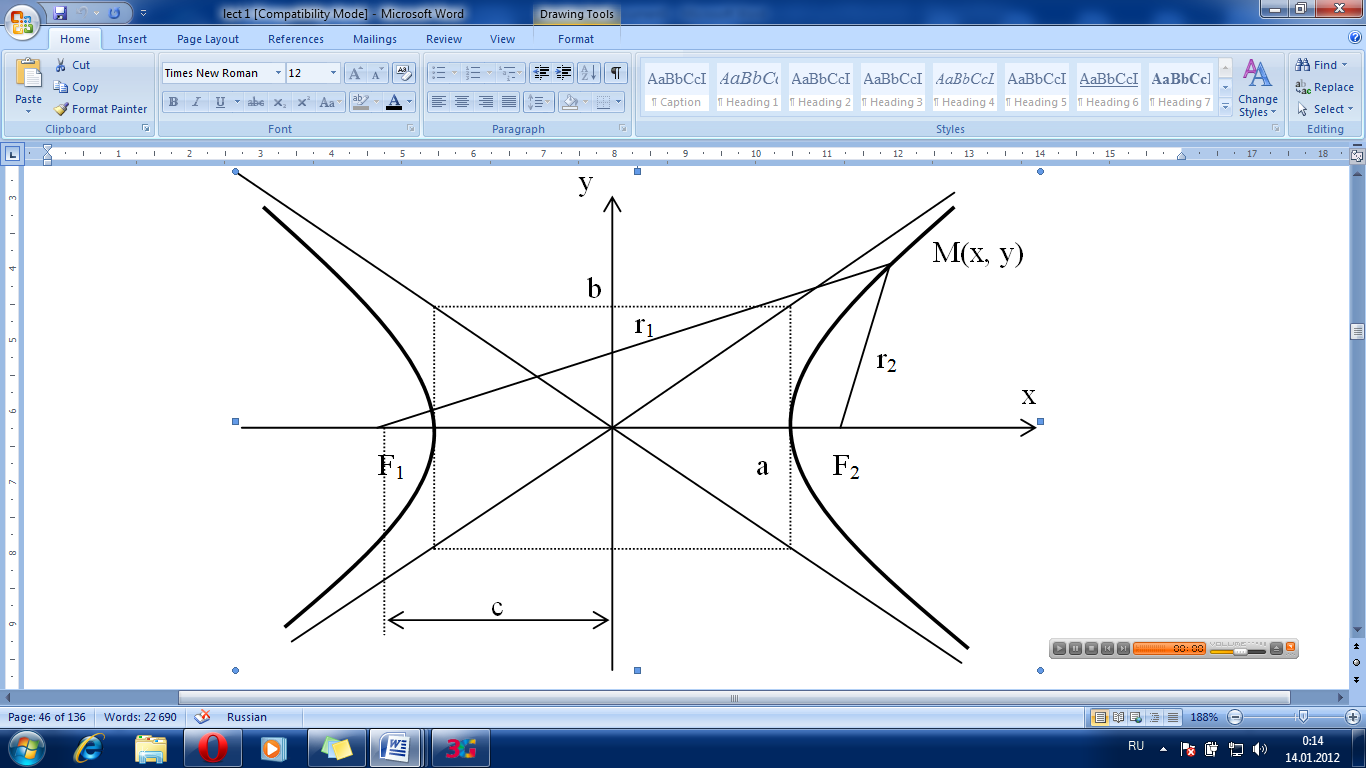

По определению ïr₁ – r₂ï= 2a. F₁, F₂ – фокусы гиперболы. F₁F₂ = 2c.

Выберем на гиперболе произвольную точку М(х, у). Тогда:

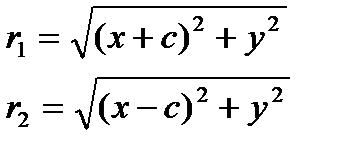
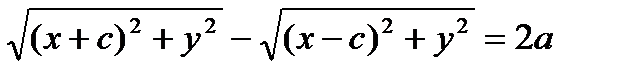
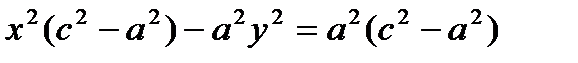
обозначим с² – а² = b² (геометрически эта величина – меньшая полуось)

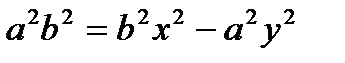
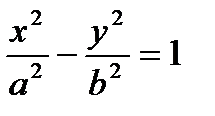
Получили каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

Ось 2а называется действительной осью гиперболы.

Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых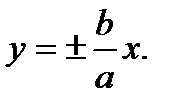

Отношение 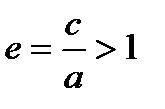называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

Если а = b, e = 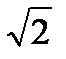, то гипербола называется равнобочной (равносторонней).

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .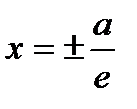

Теорема.Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу.

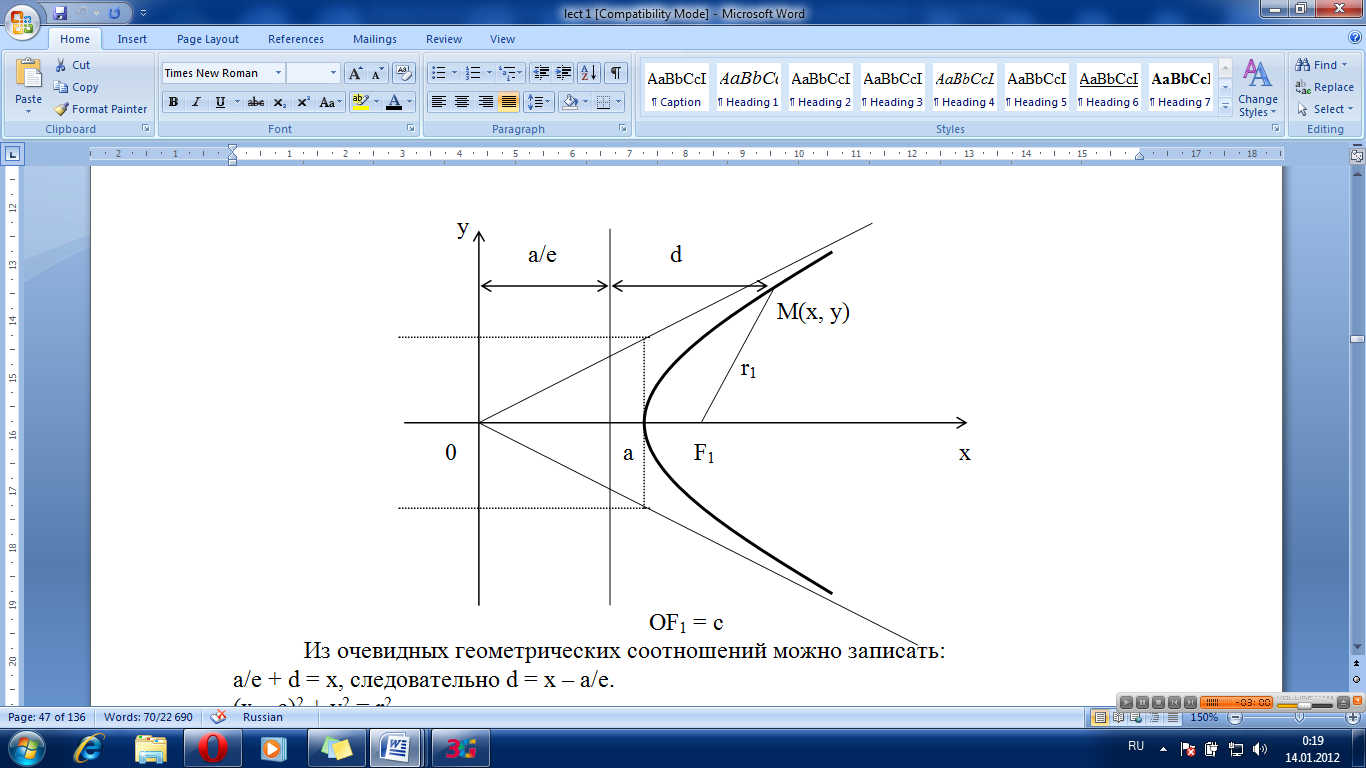
Из очевидных геометрических соотношений можно записать:

a/e + d = x, следовательно d = x – a/e.

(x – c)² + y² = r²

Из канонического уравнения: 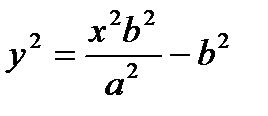, с учетом b² = c² – a²:

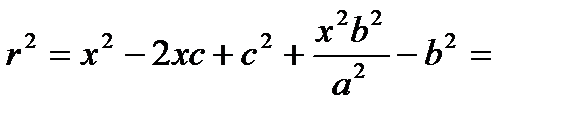
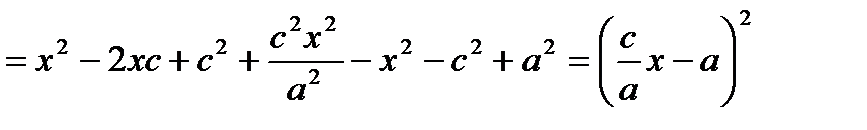
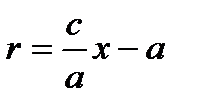
Тогда т.к. с/a = e, то r = ex – a.

Итого: .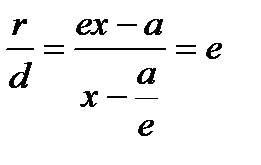

Для левой ветви гиперболы доказательство аналогично. Теорема доказана.

Парабола.

Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Расположим начало координат посередине между фокусом и директрисой.

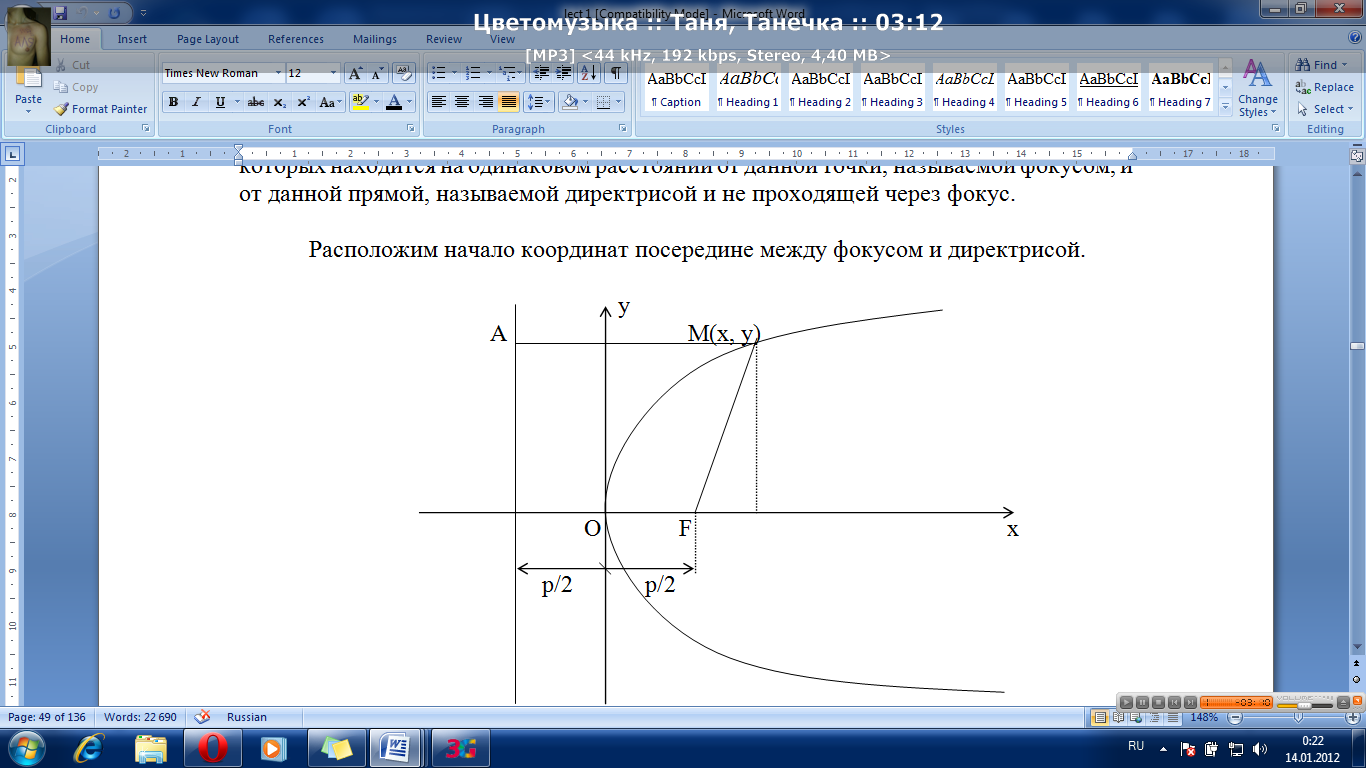
Величина р (расстояние от фокуса до директрисы) называется параметромпараболы. Выведем каноническое уравнение параболы.

Из геометрических соотношений: AM = MF; AM = x + p/2;

MF² = y² + (x – p/2)²

(x + p/2)² = y² + (x – p/2)²

x² +xp + p²/4 = y² + x² – xp + p²/4

y² = 2px

Уравнение директрисы: x = -p/2.

Сфера: .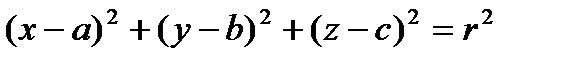

24.Последоваетльность. Предел последовательности. Число е.

Определение: Пусть каждому натуральному числу n поставлено в соответствие некоторое действительное число x_n, тогда говорим, что задана числовая последовательность (x_n). Числовые последователдьности записывают также (x_n)=x₁ ,x₂ ,x₃….

x_n– называют n-нымили общим членом последовательности.

Определение.Число называется пределом последовательности {x_n}, если для любого положительного e>0 существует такой номер N, что для всех n>N выполняется условие: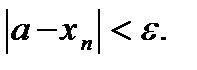

Это записывается: limx_n = a.

В этом случае говорят, что последовательность {x_n}сходитсяка при n®¥.

Если при нахождении пределов получается , то оно наз. неопределённостью. Для нахождения таких пределов требуется раскрытьнеопределённость. Последовательности, имеющие конечный предел наз. сходящимися.

Свойство:Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Необходимое условие сходимости даёт: если последовательность (x_n)сходится, то она ограничена.

Достаточное условие сходимости даёт: если последовательность (x_n) ограничена и монотонна, то она сходится.

Теорема.Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность {x_n}имеет два предела a и b, не равные друг другу.

x_n®a; x_n®b; a¹b.

Тогда по определению существует такое число e>0, что

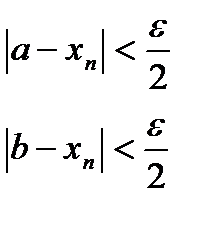
Запишем выражение: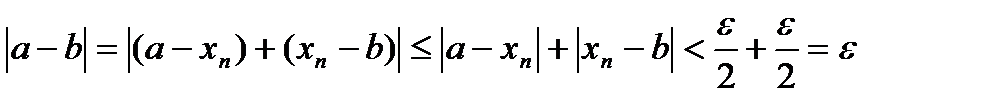

А т.к. e- любоечисло, то 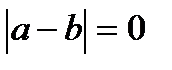, т.е. a = b. Теорема доказана.

Теорема.Если x_n®a, то .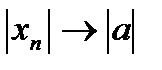

Доказательство. Из x_n®a следует, что 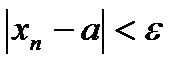. В то же время:

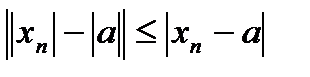, т.е. 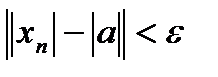, т.е. 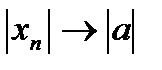. Теорема доказана.

Теорема.Если x_n®a, то последовательность {x_n} ограничена.Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность 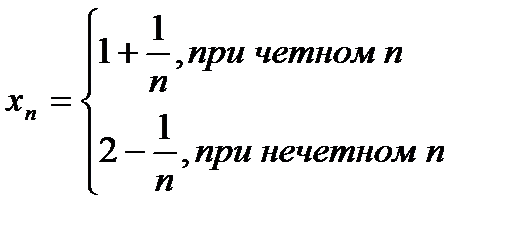не имеет предела, хотя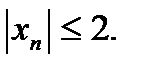

Число е- нерациональное, е ≈ 2,7. В математике число е играет важную роль. Логарифмы по основанию е наз. натуральными.