Монотонные последовательности

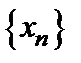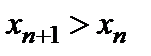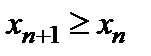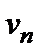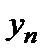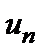Последовательность называется возрастающей (неубывающей), если для любого n выполняется неравенство ( ). Аналогичноопределяется убывающая (невозрастающая) последовательность. Возрастающая и убывающая (неубывающая и невозрастающая) последовательности называются монотоннымипоследовательностями. Последовательности { }, { } и { } – монотонные, а { 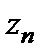} – не монотонная (см. п.1.1⁰). Отметим, что члены последовательности { 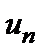} с увеличением 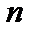неограниченно приближаются к числу 1. В этом случае говорят, что последовательность { 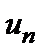}, , 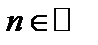стремится к пределу 1.

Теорема 1 (Вейерштрасса).Всякая монотонная ограниченная последовательность имеет предел.Число е.Примером монотонной ограниченной последовательности является последовательность 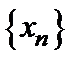, где 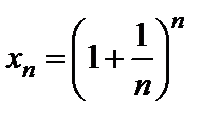. Покажем, что эта последовательность возрастающая. Действительно, с помощью формулы бинома Ньютона можно записать:

.

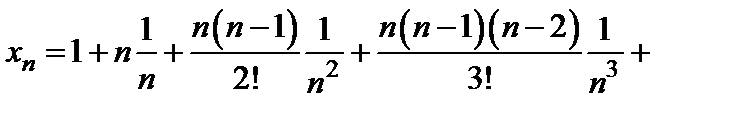
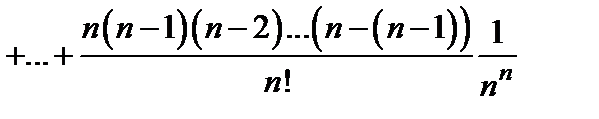Преобразуем полученное выражение следующим образом:

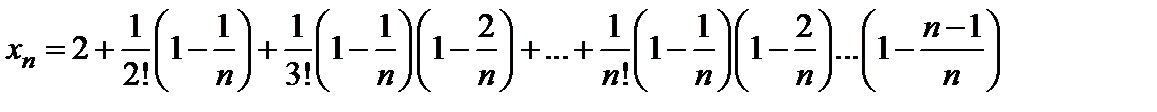. (5)

Теперь запишем по этой же формуле 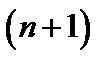-ый член:

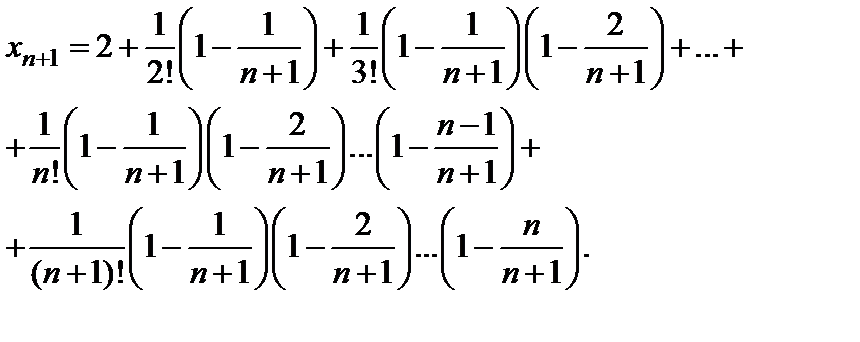
Сравним члены последовательност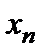и и 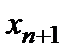. Очевидно, что 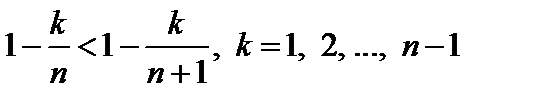. Поэтому, первые n слагаемых у 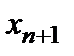не меньше соответствующих слагаемых у 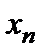. Учитывая, что 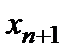содержит еще одно дополнительное неотрицательное слагаемое, получим, что .

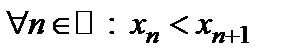Далее докажем, что рассматриваемая последовательность 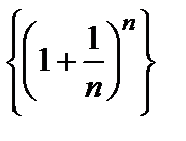ограничена. Снова воспользуемся формулой (5). Очевидно, имеет место неравенство .

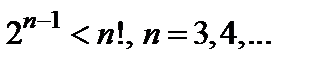Поэтому, из соотношения (5), будем иметь:

.

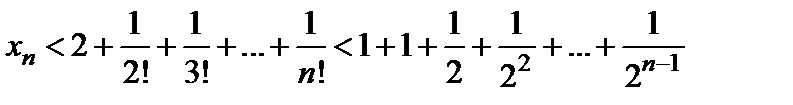Применим формулу суммы бесконечно убывающей геометрической прогрессии и получим

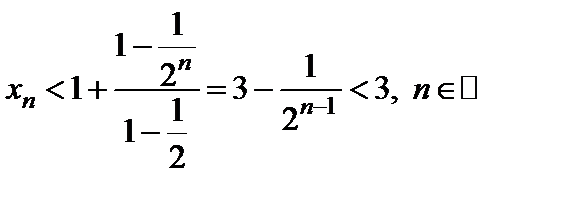. (6)

Следовательно, последовательность 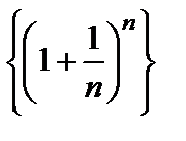– возрастающая и ограниченная, и, по теореме Вейерштрасса, имеет предел. Этот предел обозначают буквой 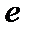и называют числом Эйлера, .

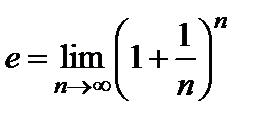Логарифмы по основанию е называют натуральными логарифмами ( 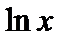). Из соотношений (5) и (6) вытекает, что 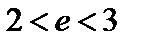. Можно доказать, что число е является иррациональным, е =2,7182… . Число е широко используется в математике и ее приложениях.

36. Предел функции в точке и на бескон.Число А назыв. Пределом функции у=f(x), в точке Xo, если для любой последоват.(Хn) принадлежащие D(y), n принадлежит N имеющ.в своих пределах точку Хо, то есть предел числа Хn и стремящееся к бесконечности равно Хo, последоват.(f(Xn)) имеет в своих пределах большое число A, то есть 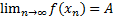. Если 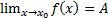и А- дейсвит.число, то говорят, что в точке Хо функция у=f(x) имеет конечный предел равный А. Пусть функция у=f(x) определена в нек. ε-окрестности точки Хо за исключением Хо. Сформулируем определ. предела ф-ции в терминах окрестности и называемым определение предела ф-ции по Коши. Число А-предел функции у=f(x) в точке Хо (при x→x₀), где x₀ÎR, если для любого ε˃0 сущ. 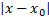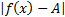δ=δ(ε)˃0, для всех x, ˂δ→ ˂ε,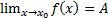

Гео.предел А функции у=f(x) при Х стремящейся к Хо означает, что какую бы горизонтальную Е полосу мы не взяли симметричную вдоль прамой у=А, всегда найдется дельта полоса симметричная прямой Х=Хо, такая что все точки графика функции расположенные в вертикальной полосе, кроме быть может точки наход.на прямой Х=Хо обязательно попадет в горизонтальную полосу. При изучении ф-ций иногда оказывается полезным рассмотреть пределы на мн-вах являющихся частями множеств определенияф-ций и лежащими по одну сторону от точки в кот. рассм. предел. Такие пределы назыв. односторонними. Это понятие содержательно лишь тогда, когда x₀ÎR.

37 БМиББ последоват.Последоват (Xn) наз.БМП, если Xn, при n стремящееся к бесконечности равен нулю. Св-ва БМП: сумма и произв.конесного числа БМП есть БМП; произв. БМП на постоянную и произведение БМП на ограниченную последоват.есть БМП; связь числовой последовательности ее предела и БМП: числовая последов.(Хn) имеет своим пределом число а, тогда, когда Хn можно представить в виде x_n=a+α_n, где α_n – б.м.п.

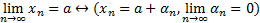
Числовая последов. (x_n) назыв. ББ если для любого сколь угодно большого числа А>0 сущ.такой номер N, что для всех n>N выполняется нер-во|Xn|>A, в этом случае пишут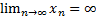

Между БМП и ББП сущ. простая связь, кот. выражает сл теорема: если (x_n) – б.м.п., 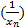- б.б.п.; если (x_n) – б.б.п., то 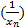– б.м.п. В этой связи в теории пределов объяснимы рав-ва 1/0=∞, 1/∞=0.

.