Интеграл по комплексному переменному
Пусть  - непрерывная функция комплексного
- непрерывная функция комплексного  , определенная в области
, определенная в области  и
и  - гладкая кривая, лежащая в
- гладкая кривая, лежащая в  , с началом в точке
, с началом в точке  и концом в точке
и концом в точке  (рис. 137), заданная уравнением
(рис. 137), заданная уравнением


или, что все равно, двумя уравнениями

 . (1)
. (1)

Рис. 137
Как всегда, направление на  соответствует изменению параметра
соответствует изменению параметра  от
от  до
до 
 .
.
Интеграл от функции  вдоль кривой
вдоль кривой  определяется следующим образом:
определяется следующим образом:


 .
.
Если учесть, что  и
и  , то равенство (2) можно коротко записать так:
, то равенство (2) можно коротко записать так:
 . (3)
. (3)
Таким образом, из (2) видно, что интеграл по комплексному переменному есть сумма двух криволинейных интегралов, и его вычисление сводится к вычислению обыкновенных интегралов.
Интеграл (2) существует для любой непрерывной функции  (в этом случае функции
(в этом случае функции  и
и  также непрерывны) и любой гладкой кривой
также непрерывны) и любой гладкой кривой  (т. е. когда
(т. е. когда  ,
,  ) непрерывны и
) непрерывны и  ).
).
Если кривая  кусочно-гладкая и состоит из гладких ориентированных кусков
кусочно-гладкая и состоит из гладких ориентированных кусков  , то по определению считаем
, то по определению считаем
 . (4)
. (4)
На основании свойств криволинейного интеграла легко получаем
1)
 ,
,
где  та же кривая, что и
та же кривая, что и  , но ориентированная противоположно (см. нашу книгу «Высшая математика. Дифференциальное и интегральное исчисление», § 7.4).
, но ориентированная противоположно (см. нашу книгу «Высшая математика. Дифференциальное и интегральное исчисление», § 7.4).
2)
 ,
,
где  - постоянные числа.
- постоянные числа.
3)
Если  при
при  , то
, то
 ,
,
где  - длина
- длина  .
.
В самом деле, на основании свойства обыкновенного интеграла имеем

 .
.
Теорема Коши. Интеграл Коши
Результат, полученный в примере 3-5, является частным случаем теоремы Коши и, если 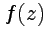 является аналитической (или только дифференцируемой) функцией в области
является аналитической (или только дифференцируемой) функцией в области 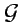 комплексной плоскости, то интеграл по любой замкнутой кривой
комплексной плоскости, то интеграл по любой замкнутой кривой  от
от 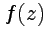 равен нулю:
равен нулю:
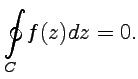 | (48) |
Теорема Коши имеет несколько важных следствий:
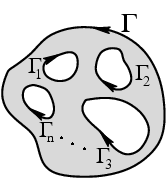 |  интеграл от интеграл от 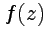 не зависит от пути интегрирования, а определяется только значениями начальной и конечной точек (см. пример 3-5 для аналитической функции не зависит от пути интегрирования, а определяется только значениями начальной и конечной точек (см. пример 3-5 для аналитической функции 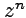 ); );  если если 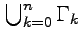 - объединенная граница многосвязной области (рис.17), то имеет место формула - объединенная граница многосвязной области (рис.17), то имеет место формула | ||
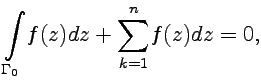 | (49) | ||
| Рис.17 | |||
где все участки границы обходятся в положительном направлении, т. е. когда захватываемая область остается слева при движении вдоль каждой кривой  ;
;
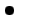 значение интеграла
значение интеграла 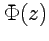 от функции
от функции 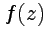 по некоторой кривой, соединяющей точки
по некоторой кривой, соединяющей точки 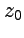 и
и 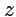 , т. е.:
, т. е.:
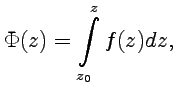 | (50) |
будет аналитической функцией переменной 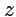 , причем
, причем 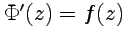 . Функция
. Функция 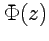 (50) называется первообразной, и для нее имеет место комплексный аналог формулы Ньютона-Лейбница:
(50) называется первообразной, и для нее имеет место комплексный аналог формулы Ньютона-Лейбница:
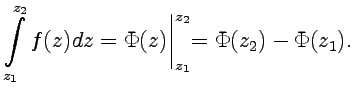 | (51) |
Ряд Лорана
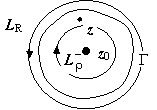
Ряд Лорана. Пусть функция f(z) аналитична в кольце ρ ≤ |z − z0| ≤ R. Тогда для любой точки этого кольца 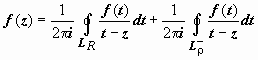 ; при этом окружности проходятся так, что область остаётся слева (следствие 3 раздела 19.7.2. Интегральная формула Коши). Изменим в интеграле по внутренней окружности направление обхода на противоположное:
; при этом окружности проходятся так, что область остаётся слева (следствие 3 раздела 19.7.2. Интегральная формула Коши). Изменим в интеграле по внутренней окружности направление обхода на противоположное: 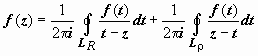 . Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора:
. Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора: 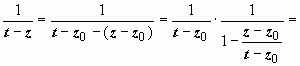 (так как | z – z0| < | t – z0| , то
(так как | z – z0| < | t – z0| , то 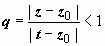 )
) 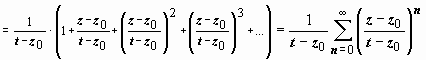 , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:
, и ряд сходится абсолютно, поэтому его можно почленно интегрировать: 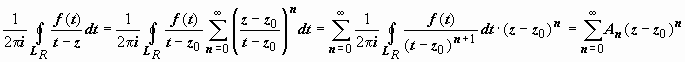 , где
, где 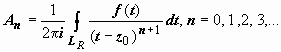 . Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на Lρ | t – z0| < | z – z0| :
. Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на Lρ | t – z0| < | z – z0| : 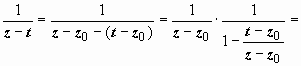
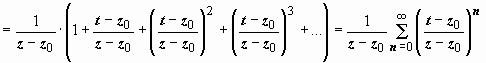 . И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать:
. И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать: 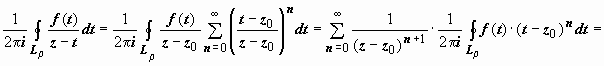
 ,
,  где
где 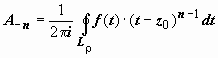 . Переобозначим n → −n, тогда форма коэффициентов ряда для Lρ совпадёт с формой коэффициентов ряда для LR:
. Переобозначим n → −n, тогда форма коэффициентов ряда для Lρ совпадёт с формой коэффициентов ряда для LR: 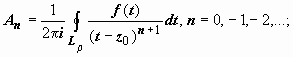 поэтому окончательно для интеграла по Lρ получим
поэтому окончательно для интеграла по Lρ получим 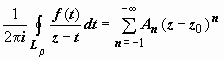 . Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть Γ - кусочно-гладкий контур, расположенный в кольце ρ ≤ |z − z0| ≤ R, и точка z0 расположена внутри этого контура. По теореме Коши для многосвязной области
. Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть Γ - кусочно-гладкий контур, расположенный в кольце ρ ≤ |z − z0| ≤ R, и точка z0 расположена внутри этого контура. По теореме Коши для многосвязной области 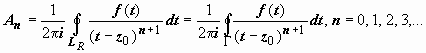 ;
; 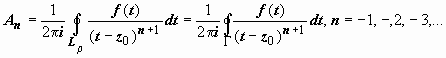 , поэтому для любого n
, поэтому для любого n 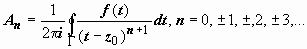 , и
, и
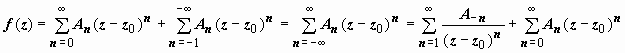 .
.
Этот ряд (содержащий и положительные, и отрицательные степени (z – z0), называется рядом Лорана функции f(z). Его часть, содержащая неотрицательные степени ( 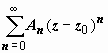 ), называется правильной; часть, содержащая отрицательные степени (
), называется правильной; часть, содержащая отрицательные степени ( 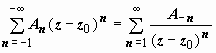 ), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z0| ≤ R, главная - во внешности круга | z – z0| ≥ ρ, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце ρ ≤ | z – z0| ≤ R. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.
), называется главной. Правильная часть, по самому своему построению, сходится в круге | z – z0| ≤ R, главная - во внешности круга | z – z0| ≥ ρ, поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце ρ ≤ | z – z0| ≤ R. Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.
Еще раз подчеркнем, что в ряд Лорана раскладывается функция, аналитическая в кольце, и ширина этого кольца определяется областью аналитичности функции, т.е. разложение теряет смысл там, где функция теряет аналитичность. Рассмотрим
