Признаки сравнения. Признак Даламбера.
(Признак Даламбера) Допустим, что строго положительный ряд (29) таков, что существует (конечный или бесконечный) предел
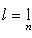
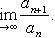 (30)
(30)
Тогда при l > 1 ряд (28) расходится, а при l < 1 сходится.
Допустим сначала, что l > 1. Так как дробь 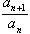 стремится к l, то достаточно далекие значения этой дроби будут удовлетворять неравенству
стремится к l, то достаточно далекие значения этой дроби будут удовлетворять неравенству
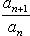
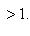 (31)
(31)
Пусть, например, это неравенство выполнено для всех n, удовлетворяющих неравенству n > m. Тогда ряд
am+1 + am+2 + am+3 + ... (32)
таков, что у него отношение уже любого последующего члена к своему предыдущему оказывается удовлетворяющим неравенству (31). Значит (по лемме 1), ряд (32) расходится, а так как это есть остаток ряда (28), то этот последний ряд также расходится.
Пусть теперь l < 1. Закрепим какое-нибудь число q, удовлетворяющее неравенству l < q < 1 (например, положим 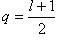 ). Тогда найдется такое m, что при всехn > m будет
). Тогда найдется такое m, что при всехn > m будет
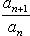
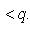
Снова составляя ряд (32) и применяя к нему лемму 2, убеждаемся сначала в сходимости ряда (32), а затем и ряда (28).
Доказанная теорема действительно имеет совершенно алгорифмический характер: для ее применения надо лишь составить отношение 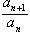 и изучить его поведение при безгранично возрастающем n. Никаких вспомагательных рядов для сопоставления с данным рядом искать уже не требуется. Надо заметить, однако, что теорема 3 применима далеко не всегда. Не говоря уже о том, что предела (30) может не существовать, этот предел может равняться 1, и тогда теорема также не позволяет сделать никакого заключения относительно сходимости ряда.
и изучить его поведение при безгранично возрастающем n. Никаких вспомагательных рядов для сопоставления с данным рядом искать уже не требуется. Надо заметить, однако, что теорема 3 применима далеко не всегда. Не говоря уже о том, что предела (30) может не существовать, этот предел может равняться 1, и тогда теорема также не позволяет сделать никакого заключения относительно сходимости ряда.
Признак сравнения. Признак коши
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда
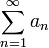
с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство 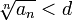 , то данный ряд сходится.
, то данный ряд сходится.
Предельная форма
Условие радикального признака равносильно следующему:
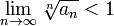
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Если для ряда
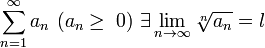 , то
, то
если 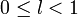 ряд сходится,
ряд сходится,
если l > 1 ряд расходится,
если l = 1 вопрос о сходимости ряда остается открытым.
Интегральные сходимости знакопостоянных рядов
Интегральный признак Коши
Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд
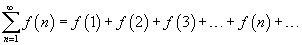 сходится, если сходится несобственный интеграл
сходится, если сходится несобственный интеграл 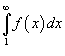 , и расходится, если
, и расходится, если 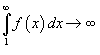 .
.
Формулировка теоремы
Пусть для функции f(x) выполняется: 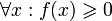 (функция принимает неотрицательные значения) (функция принимает неотрицательные значения) 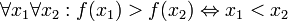 (функция монотонно убывает) (функция монотонно убывает) 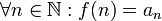 (соответствие функции ряду) Тогда ряд (соответствие функции ряду) Тогда ряд 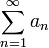 и несобственный интеграл и несобственный интеграл 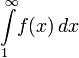 сходятся или расходятся одновременно. сходятся или расходятся одновременно. |
Знакочередующиеся ряды. Теорема Лейбница
Знакочередующиеся ряды
Переходя к рассмотрению рядов, члены которых уже не обязательно положительны, остановимся сначала на одном важном частном типе этих рядов - на рядах знакочередующихся, теория которых сравнительно проста.
Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков.
Несколько изменяя употреблявшуюся выше символику, будем обозначать через an не сам общий член ряда, а его абсолютную величину. Тогда, предполагая для определенности, что первый член знакочередующегося ряда положителен, мы сможем записать этот ряд в форме*
a1 - a2 + a3 - a4 + a5 - ... (36)
Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.
Действительно, допустим, что ряд (36) таков, что
a1 > a2 > a3 > a4 > ..., (37)
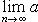
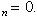 (38)
(38)
Образуем частичные суммы S2n:
S2 = (a1 - a2),
S4 = (a1 - a2) + (a3 - a4),
S6 = (a1 - a2) + (a3 - a4) + (a5 - a6),
. . . . . . . . . . . . . .
Благодаря (37), все скобки положительны. Значит,
S2 < S4 < S6 < ...
Иначе говоря, последовательность {S2n} возрастает. С другой стороны,
S2n = a1 - (a2 - a3) - (a4 - a5) - ... - (a2n-2 - a2n-1) - a2n,
откуда ясно, что
S2n < a1.
Как известно, при этих условиях существует конечный предел
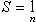
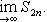
Но
S2n+1 = S2n + a2n+1,
откуда в связи с (38) вытекает, что сумма S2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма Sn будет сколь угодно близка к Sнезависимо от четности n. Иначе говоря,
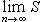
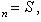
чем и доказана теорема.
Заметим, что теорема перестает быть верной, если отбросить условие убывания an. Например, знакочередующийся ряд
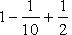
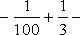
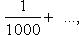
как легко видеть, расходится
