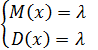Показательное распределении вероятностей непрерывных СВ. Функция надежности.

Опр.: Говорят, что НСВ имеет покозат. (экспонентц.) распределение, если плотность вероятностей имеет вид:

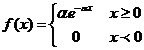
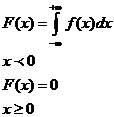
Найдем математические характеристики:

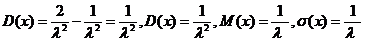
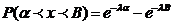
Функция надежности.

функция распределения F(t)=P(T<t)=1- e-mt определяет вероятность отказа устройства за время t.

Найдем вероятность противоположного события- безотказной работы за время t:

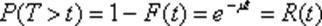
Функция R(t) называется функцией надежности. Выясним смысл числовых характеристик и параметра распределения.

Математическое ожидание - это среднее время между двумя ближайшими отказами устройства, а величина обратная математическому ожиданию (параметр распределения)- интенсивность отказов, т.е. количество отказов в единицу времени.

Проверка гипотезы о нормальном распределении генеральной совокупности.Критерий согласия.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины – критерия согласия.

Критерий согласия (хи-квадрат)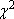

Критерий согласия 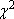разработан лучше других критериев и чаще других используется. Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения.

Порядок, применения:

1. Формулируется гипотеза, выбирается уровень значимости a.

2. Получается выборка объема n 40 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.

3. Рассчитываются выборочные характеристики 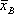и S.

4. Вычисляются значения теоретических частот :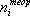

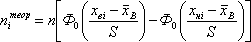
где Ф0(u) — функции Лапласа, xвi и хнi — верхняя и нижняя границы i-го интервала группировки.

5. Соответственно складываются и эмпирические частоты объединяемых интервалов.

5. Значение 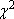-критерия рассчитывается по формуле: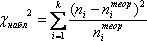

где ni — эмпирические частоты; 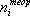– ожидаемые (теоретические) частоты; k — число интервалов группировки после объединения.

6. Из таблиц распределения 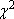находится критическое значение 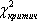критерия для уровня значимости а и числа степеней свободы n=n–3.

7. Вывод: если 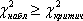то эмпирическое распределение не соответствует нормальному распределению на уровне значимости a, в противном случае нет оснований отрицать это соответствие.

Билет 6

Повторение испытаний

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.

Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:

6.1.2. Распределение Пуассона

Говорят,что случайная величина распределена по закону Пуассона,если ее возможное значение 0,1,2,…,л… а соответственные вероятности определяться по формуле P_k=P_n(x=k)= 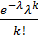, k=0,1,2,…